IMU 积分进行航迹推算

Posted 2023-05-21 weihao-ysgs

IMU 积分进行航迹推算

Reference https://github.com/gaoxiang12/slam_in_autonomous_driving

1.0 递推方程推导

\\(\\quad\\)连续时间内的 IMU 运动学方程：

\\[\\dot\\mathbfR=\\mathbfR\\omega ^\\wedge \\\\ \\dot\\mathbfq=\\frac12\\mathbfq\\omega\\\\ \\dot\\mathbfp=v \\\\ \\dot\\mathbfv=a \\]

\\(\\quad\\)这些物理量带上角标之后应该写作 \\(\\mathbfR_wb,p_wb\\)，对应世界坐标系，它在求导之后就是车辆在世界坐标系下的速度与加速度 \\(\\mathbfv_w, \\mathbfa_w\\) 。在不考虑地球自传的时候，也可以简单的将 车辆行驶的打的视为固定的世界坐标系，这时 IMU 的测量值 \\(\\widetilde\\omega ,\\widetildea\\) 就是车辆本身的角速度，以及车体系下的加速度:

\\[\\beginaligned \\tilde\\boldsymbola & =\\boldsymbolR^\\top \\boldsymbola, \\\\ \\tilde\\boldsymbol\\omega & =\\boldsymbol\\omega . \\endaligned \\]

\\(\\quad\\)注意 \\(\\mathbfR^\\top\\) 带下标之后就是 \\(\\mathbfR_bw\\)。它将世界系下的物理量转换到车体系。然而，实际的车辆、机器人都在地球表面运行。这些系统受到重力的影响，所以我们应该把重 力写在系统方程中。在绝大多数 IMU 系统中，我们可以忽略地球自转的干扰，从而把 IMU 测量 值写为：

\\[\\beginaligned \\tilde\\boldsymbola & =\\boldsymbolR^\\top \\boldsymbol(a-g), \\\\ \\tilde\\boldsymbol\\omega & =\\boldsymbol\\omega . \\endaligned \\]

\\(\\quad\\)\\(\\mathbfg\\) 为地球的重力。当然，如果在无重力环境下测量物体加速度，就不会出现重力项。注意这里 \\(\\mathbfg\\)的符号和坐标系定义相关。我们的车体系和世界系都是 \\(Z\\) 轴向上，于是 \\(\\mathbfg\\) 通常取 值 \\((0, 0, −9.8)^⊤\\)。假设有一个水平放置的IMU，其读数此时应当为 \\((0, 0, 9.8)^⊤\\)，为什么呢？因为此时真正的加速度应该为 \\((0, 0, 0)^⊤\\)，但是由于地球重力的影响，其输出结果会减去 \\(\\mathbfg\\) ，所以输出结果就是\\((0, 0, 9.8)^⊤\\)。

\\(\\quad\\)在大多数系统中，我们认为 IMU 的噪声由两部分组成：测量噪声（measurement noise）与零偏（bias）。记陀螺仪和加速度计的测量噪声分别为 \\(η_g\\), \\(η_a\\)，同时记零偏为 \\(b_g\\), \\(b_a\\)，下标 \\(g\\) 表示陀螺仪，\\(a\\) 表示加速度计。那么这几个参数在测量方程中体现为：

\\[\\beginaligned \\tilde\\boldsymbola & =\\boldsymbolR^\\top(\\boldsymbola-\\boldsymbolg)+\\boldsymbolb_a+\\boldsymbol\\eta_a \\\\ \\tilde\\boldsymbol\\omega & =\\boldsymbol\\omega+\\boldsymbolb_g+\\boldsymbol\\eta_g . \\endaligned \\]

\\(\\quad\\)于是，我们直接把测量模型代入运动学方程，忽略测量噪声影响，即可得到连续时间下的积分 模型：

\\[\\beginaligned \\dot\\boldsymbolR & =\\boldsymbolR\\left(\\tilde\\boldsymbol\\omega-\\boldsymbolb_g\\right)^\\wedge, \\quad \\text 或 \\dot\\boldsymbolq=\\boldsymbolq\\left[0, \\frac12\\left(\\tilde\\boldsymbol\\omega-\\boldsymbolb_g\\right)\\right], \\\\ \\dot\\boldsymbolp & =\\boldsymbolv, \\\\ \\dot\\boldsymbolv & =\\boldsymbolR\\left(\\tilde\\boldsymbola-\\boldsymbolb_a\\right)+\\boldsymbolg . \\endaligned \\]

\\(\\quad\\)有时候我们也把 \\(p, v, q\\) 称为 \\(PVQ\\) 状态。该方程可以从时间 \\(t\\)积分至 \\(t + ∆t\\),推出下一个时刻的状态情况:

\\[\\beginaligned \\boldsymbolR(t+\\Delta t) & =\\boldsymbolR(t) \\operatornameExp\\left(\\left(\\tilde\\boldsymbol\\omega-\\boldsymbolb_g\\right) \\Delta t\\right), \\quad \\text 或 \\boldsymbolq(t+\\Delta t)=\\boldsymbolq(t)\\left[1, \\frac12\\left(\\tilde\\boldsymbol\\omega-\\boldsymbolb_g\\right) \\Delta t\\right], \\\\ \\endaligned \\]

\\(\\quad\\)这里我们先不考虑白噪声 \\(\\boldsymbol\\eta_a\\)，则IMU的测量方程有：

\\[\\beginaligned \\tilde\\boldsymbola &=\\boldsymbolR^\\top(\\boldsymbola-\\boldsymbolg)+\\boldsymbolb_a+\\boldsymbol\\eta_a\\\\ \\tilde\\boldsymbola -\\boldsymbolb_a&=\\boldsymbolR^\\top(\\boldsymbola-\\boldsymbolg) \\\\ \\boldsymbolR(\\tilde\\boldsymbola -\\boldsymbolb_a)&=\\boldsymbola-\\boldsymbolg\\\\ \\boldsymbola&=\\boldsymbolR(\\tilde\\boldsymbola -\\boldsymbolb_a) + \\boldsymbolg \\endaligned \\]

\\(\\quad\\)速度的递推，我们知道 \\(\\boldsymbolv(t+\\Delta t) = \\boldsymbolv(t) + \\mathbfat\\)。

\\[\\beginaligned \\boldsymbolv(t+\\Delta t) & =\\boldsymbolv(t)+ \\mathbfa\\Delta t \\\\ & =\\boldsymbolv(t)+ \\left( \\boldsymbolR(t)\\left(\\tilde\\boldsymbola-\\boldsymbolb_a\\right) +\\boldsymbolg \\right)\\Delta t \\\\ &=\\boldsymbolv(t)+\\boldsymbolR(t)\\left(\\tilde\\boldsymbola-\\boldsymbolb_a\\right) \\Delta t+\\boldsymbolg \\Delta t . \\endaligned \\]

\\(\\quad\\)位置的递推，我们知道 \\(\\boldsymbolp(t+\\Delta t) =\\boldsymbolp(t)+\\mathbfv\\Delta t + \\frac12\\mathbfat^2\\)，则有：

\\[\\beginaligned \\boldsymbolp(t+\\Delta t) & =\\boldsymbolp(t)+\\boldsymbolv \\Delta t+\\frac12 \\mathbfat^2\\\\ & =\\boldsymbolp(t)+\\boldsymbolv \\Delta t+\\frac12 \\left(\\boldsymbolR(t)(\\tilde\\boldsymbola -\\boldsymbolb_a) + \\boldsymbolg \\right)t^2\\\\ & =\\boldsymbolp(t)+\\boldsymbolv \\Delta t+\\frac12\\left(\\boldsymbolR(t)\\left(\\tilde\\boldsymbola-\\boldsymbolb_a\\right)\\right) \\Delta t^2+\\frac12 \\boldsymbolg \\Delta t^2\\\\ \\endaligned \\]

2.0 代码实现

2.1 数据集介绍

这里使用的高博书中带的数据集，数据集的格式为：

# timestamp gx gy gz ax ay az

2.2 具体代码实现

代码实现主要有三个文件

• common.hpp 主要用户存放 IMU 数据结构体和读取和保存数据。
• imu_integration.hpp 主要存放 IMU数据的处理和航迹推算实现类。
• run_imu_integration.cpp 程序入口函数。

如下命令运行

./run_imu_integration --txt_file_path="../slam_in_auto_driving/chapter3/dataset/10.txt" --output_inter_trajectory_path="./output_trajectory.txt" 

• common.hpp

#ifndef COMMON_HPP
#define COMMON_HPP

#include <eigen3/Eigen/Core>
#include <eigen3/Eigen/Dense>
#include <fstream>
#include <iomanip>
#include <iostream>
#include <string>
#include <vector>

struct IMUMsg

  IMUMsg() = default;
  IMUMsg(double timestamp, Eigen::Vector3d gyro, Eigen::Vector3d acc)
      : timestamp_(timestamp), acc_(acc), gyro_(gyro);

  double timestamp_0.0;
  Eigen::Vector3d acc_;
  Eigen::Vector3d gyro_;
;

struct IMUIntegrationResult

  IMUIntegrationResult() = default;
  IMUIntegrationResult(const double &timestamp, const Eigen::Vector3d &P,
                       const Eigen::Quaterniond &Q, const Eigen::Vector3d &V)
      : timestamp_(timestamp), P_(P), V_(V), Q_(Q);

  double timestamp_0.0;
  Eigen::Vector3d P_;
  Eigen::Vector3d V_;
  Eigen::Quaterniond Q_;
;

inline void ReadImuMsg(std::ifstream &fin, std::vector<IMUMsg> &imu_msg)

  if (!fin)
  
    std::cerr << "Coule not find file\\n";
    return;
  
  while (!fin.eof())
  
    std::string line;
    std::getline(fin, line);
    if (line.empty())
    
      continue;
    

    if (line[0] == \'#\')
    
      continue;
    

    std::stringstream ss;
    ss << line;
    std::string data_type;
    ss >> data_type;
    if (data_type == "IMU")
    
      double time, gx, gy, gz, ax, ay, az;
      ss >> time >> gx >> gy >> gz >> ax >> ay >> az;
      imu_msg.push_back(IMUMsg(time, Eigen::Vector3d(gx, gy, gz),
                               Eigen::Vector3d(ax, ay, az)));
    
  
  std::cout << "Read IMU msgs success\\n";


inline void SaveImuIntegrationResult(
    const std::string &file_path,
    const std::vector<IMUIntegrationResult> &imu_inte_result)

  std::ofstream fout(file_path);
  for (const auto &imu_traj : imu_inte_result)
  
    fout << std::setprecision(18) << imu_traj.timestamp_ << " " << std::setprecision(9);
    fout << imu_traj.P_(0) << " " << imu_traj.P_(1) << " " << imu_traj.P_(2) << " ";
    fout << imu_traj.Q_.w() << " " << imu_traj.Q_.x() << " " << imu_traj.Q_.y() << " " << imu_traj.Q_.z() << " ";
    fout << imu_traj.V_(0) << " " << imu_traj.V_(1) << " " << imu_traj.V_(2) << " ";
    fout << std::endl;
  


#endif  // COMMON_HPP

• imu_integration.hpp

#include <eigen3/Eigen/Core>
#include <eigen3/Eigen/Dense>
#include <sophus/so3.hpp>

#include "common.hpp"

class ImuIntegration

 public:
  ImuIntegration() = default;
  ~ImuIntegration() = default;
  ImuIntegration(const Eigen::Vector3d &gravity, const Eigen::Vector3d &init_bg,
                 const Eigen::Vector3d &init_ba)
      : gravity_(gravity), init_ba_(init_ba), init_bg_(init_bg)
  
  

  void AddNewImgMessage(const IMUMsg &imu_msg)
  
    // Final P: -3.38794e+06  5.73752e+06  -512933
    // 其实第一帧 IMU 数据也可以不判断，因为后面有 dt<0.1 的判断
    if (first_imu_)
    
      first_imu_ = false;
      timestamp_ = imu_msg.timestamp_;
    

    double dt = imu_msg.timestamp_ - timestamp_;

    if (dt > 0 && dt < 0.1)
    
      P_ = P_ + V_ * dt + 0.5 * (R_ * (imu_msg.acc_ - init_ba_)) * dt * dt +
           0.5 * gravity_ * dt * dt;
      V_ = V_ + R_ * (imu_msg.acc_ - init_ba_) * dt + gravity_ * dt;
      R_ = R_ * Sophus::SO3d::exp((imu_msg.gyro_ - init_bg_) * dt);
    

    timestamp_ = imu_msg.timestamp_;
  

  Eigen::Vector3d GetPosition() const  return P_; 
  Eigen::Vector3d GetVelocity() const  return V_; 
  Eigen::Quaterniond GetRotation() const  return R_.unit_quaternion(); 

 private:
  Sophus::SO3d R_;
  Eigen::Quaterniond R_quaternion_ = Eigen::Quaterniond::UnitRandom();
  Eigen::Vector3d P_ = Eigen::Vector3d::Zero();
  Eigen::Vector3d V_ = Eigen::Vector3d::Zero();
  Eigen::Vector3d gravity_ = Eigen::Vector3d(0, 0, -9.81);
  Eigen::Vector3d init_ba_ = Eigen::Vector3d::Zero();
  Eigen::Vector3d init_bg_ = Eigen::Vector3d::Zero();
  double timestamp_0.0;
  bool first_imu_true;
;

• run_imu_integration.cpp

#include <gflags/gflags.h>

#include <eigen3/Eigen/Core>
#include <eigen3/Eigen/Dense>
#include <iostream>
#include <ostream>

#include "common.hpp"
#include "imu_integration.hpp"

DEFINE_string(txt_file_path, "../slam_in_auto_driving/chapter3/dataset/10.txt",
              "Imu integration file");
DEFINE_string(output_inter_trajectory_path, "./output_trajectory.txt",
              "output trajectory file");

int main(int argc, char *argv[])

  google::ParseCommandLineFlags(&argc, &argv, true);
  std::ifstream fin(FLAGS_txt_file_path);
  std::vector<IMUMsg> imu_msgs;
  std::vector<IMUIntegrationResult> imu_inter_result;
  ReadImuMsg(fin, imu_msgs);

  // 该实验中，我们假设零偏已知
  Eigen::Vector3d gravity(0, 0, -9.8);  // 重力方向
  Eigen::Vector3d init_bg(00.000224886, -7.61038e-05, -0.000742259);
  Eigen::Vector3d init_ba(-0.165205, 0.0926887, 0.0058049);

  ImuIntegration imu_integration(gravity, init_bg, init_ba);

  for (auto &imu_msg : imu_msgs)
  
    imu_integration.AddNewImgMessage(imu_msg);
    imu_inter_result.push_back(IMUIntegrationResult(
        imu_msg.timestamp_, imu_integration.GetPosition(),
        imu_integration.GetRotation(), imu_integration.GetVelocity()));
  

  SaveImuIntegrationResult(FLAGS_output_inter_trajectory_path,
                           imu_inter_result);
  // 高博书中程序输出的结果
  // T: 1624429630.2702086
  // P : -3387943.36 5737523.81 -512933.307
  // Q : 0.982857044 -0.132676506 0.0940114453 0.0868954789
  // V : -572.166705 4626.10758 -496.605214
  std::cout << "Final P: " << imu_integration.GetPosition().transpose()
            << std::endl;
  std::cout << "Final V: " << imu_integration.GetVelocity().transpose()
            << std::endl;
  std::cout << "Final Q: " << imu_integration.GetRotation().coeffs().transpose()
            << std::endl;

  return 0;

输出结果可视化：

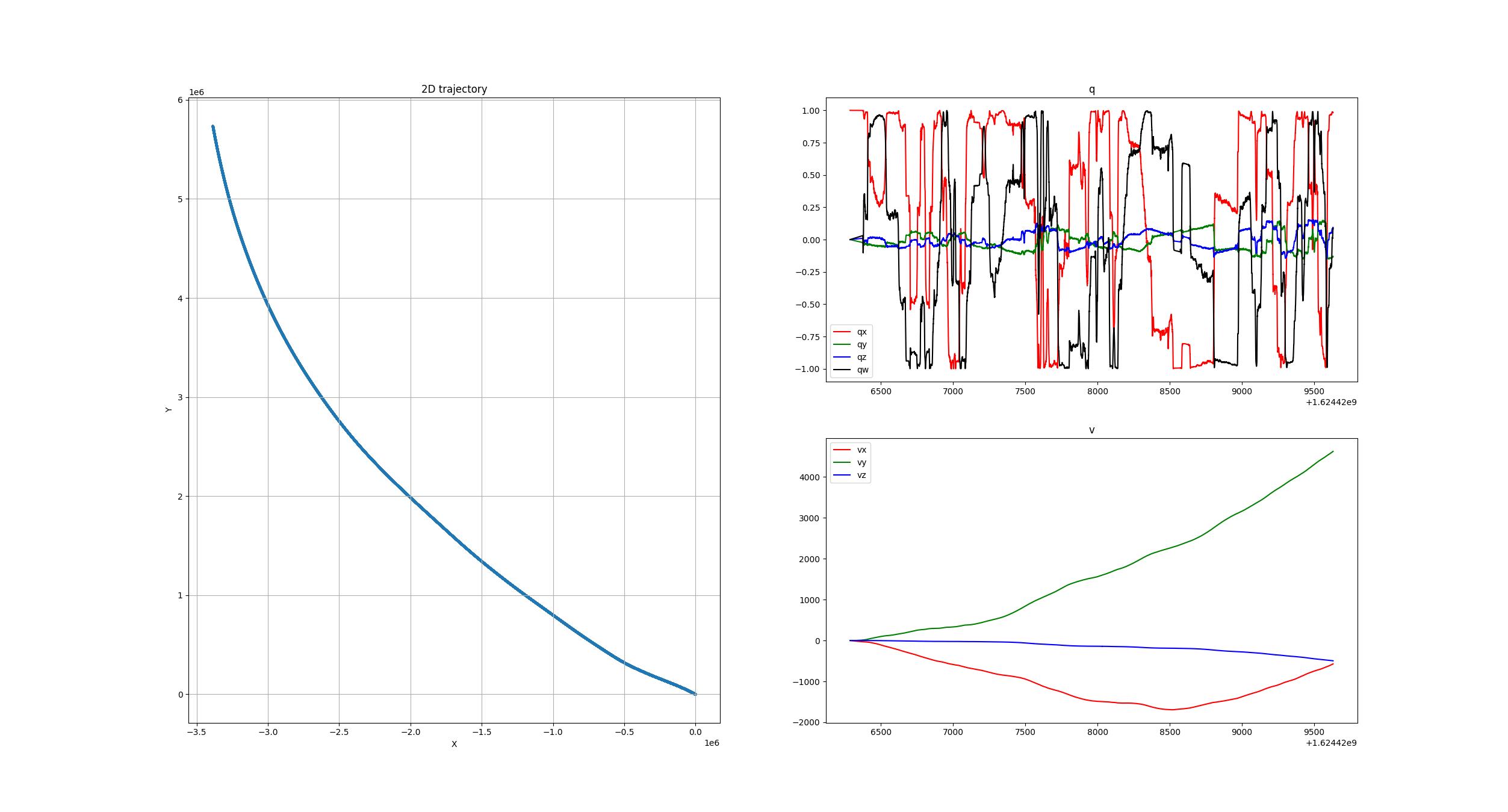
可视化程序，运行：

python3 draw_imu_integration.py ./output_trajectory.txt 

# coding=UTF-8
import sys
import numpy as np
import matplotlib.pyplot as plt

if __name__ == "__main__":
    if len(sys.argv) != 2:
        print(\'Please input valid file\')
        exit(1)
    else:
        path = sys.argv[1]
        path_data = np.loadtxt(path)
        plt.rcParams[\'figure.figsize\'] = (16.0, 12.0)
        
        # 轨迹
        plt.subplot(121)
        plt.scatter(path_data[:, 1], path_data[:, 2], s=2)
        plt.xlabel(\'X\')
        plt.ylabel(\'Y\')
        plt.grid()
        plt.title(\'2D trajectory\')
        
        # 姿态
        plt.subplot(222)
        plt.plot(path_data[:, 0], path_data[:, 4], \'r\')
        plt.plot(path_data[:, 0], path_data[:, 5], \'g\')
        plt.plot(path_data[:, 0], path_data[:, 6], \'b\')
        plt.plot(path_data[:, 0], path_data[:, 7], \'k\')
        plt.title(\'q\')
        plt.legend([\'qx\', \'qy\', \'qz\', \'qw\'])

        # 速度
        plt.subplot(224)
        plt.plot(path_data[:, 0], path_data[:, 8], \'r\')
        plt.plot(path_data[:, 0], path_data[:, 9], \'g\')
        plt.plot(path_data[:, 0], path_data[:, 10], \'b\')
        plt.title(\'v\')
        plt.legend([\'vx\', \'vy\', \'vz\'])

        plt.show()
        exit(1)

IMU 预积分推导

给 StereoDSO 加 IMU，想直接用 OKVIS 的代码，但是有点看不懂。知乎上郑帆写的文章《四元数矩阵与 so(3) 左右雅可比》提到 OKVIS 的预积分是使用四元数，而预积分论文中使用 so(3) 的右雅克比。才疏学浅，先整理好 so(3) 的预积分，写好 StereoDSO 加上 IMU，再考虑其他的东西。
以下的内容参考预积分的的论文，还有它的 Supplementary Material。预积分的论文中有一些 typo 所以看上去还是比较迷的，参考网络上多份预积分论文的 pdf，我整理一下整个预积分的推导过程。所以以下内容也可以看做是预积分内容的翻译。

预积分的意义。IMU 测量设备的角速度、线加速度，通过积分可以获得设备在一段时间内的位置、姿态、速度改变量，积分是在 Manifold 上进行，所以不同积分起点，位置、姿态、速度改变量也不同。在 VIO 的应用过程中，需要将 IMU 误差进入到优化过程，优化迭代计算。由于以上 Manifold 的特性，使得每次优化起点发生变化，IMU 测量得到的相对位置、姿态、速度发生变化，所以每次优化迭代需要对 IMU 测量值重新积分，过程耗时。为了解决这个不断积分的问题，IMU 预积分不将位置、姿态、速度改变量作为 IMU 观测值，而将重力加速度对它们的影响去除（公式 (\ref{eq2:imu_pre_state_diff_delta_R_ij}) (\ref{eq2:imu_pre_state_diff_delta_v_ij}) (\ref{eq2:imu_pre_state_diff_delta_p_ij})），使得新定义的 IMU 观测值与起点的位置、姿态、速度无关，在优化过程中不会因为起点的这些状态量改变而重新积分。（去除重力加速度的影响，应是重力加速度与当前的姿态相关，只有将其去除才有可能使得 IMU 观测值与起点的姿态无关。）但是定义的 IMU 观测值依旧与起点的偏移值相关，使用 Taylor 展开拟合偏移值在优化过程中的变化，累积到足够大再进行积分。

我写这个东西，就是瞎bb，代码还没有验证。

---

DSO 是左雅克比（看这个代码就知道了，https://github.com/JakobEngel/dso/blob/master/src/FullSystem/HessianBlocks.h#L190 ），而 IMU 预积分论文是右雅克比。需要注意在特定的地方改变一下。

Residuals

IMU 测量值可以看做真实值、漂移值（Bias）、高斯误差的和：
\[\begin{align} \mathbin{_B\tilde{\pmb{\omega}}_{WB}}(t) = \mathbin{_B\pmb{\omega}_{WB}}(t) + \pmb{b}^g(t) + \pmb{\eta}^g(t) \label{eq2:imu_pre_mes_w} \\mathbin{_B\tilde{\pmb{a}}}(t) = \mathbf{R}_{WB}^T(t)(\mathbin{_W\pmb{a}}(t) - \mathbin{_W\pmb{g}}) + \pmb{b}^a(t) + \pmb{\eta}^a(t) \label{eq2:imu_pre_mes_a} \end{align}\]
其中下标的 \(W, B\) 分别表示世界（World）坐标系和 IMU （Body）坐标系，左下标 \(\mathbin{_W\cdot}, \mathbin{_B\cdot}\) 表示所在的坐标系，\(\mathbf{R}_{WB}\) 的右下标表示从 IMU 坐标系旋转到世界坐标系，\(\mathbin{_B\pmb{\omega}_{WB}}\) 的右下标表示 IMU 坐标系相对于世界坐标系的瞬时角速度，右上标 \(\cdot^{g}, \cdot^{a}\) 分别表示陀螺仪（Gyroscope）角速度测量值相关、加速度计（Accelerometer）线加速度测量值相关。公式中的真实值是 \(t\) 时刻的角速度 \(\mathbin{_B\pmb{\omega}_{WB}}(t)\)、线加速度 \(\mathbin{_W\pmb{a}}(t)\)，漂移值是 \(t\) 时刻的角速度漂移值 \(\pmb{b}^g(t)\)、线加速度漂移值 \(\pmb{b}^a(t)\)，高斯误差是 \(t\) 时刻的角速度测量值误差 \(\pmb{\eta}^g(t)\)、线加速度测量误差 \(\pmb{\eta}^a(t)\)。\(\mathbin{_W\pmb{g}}\) 是世界坐标系下的重力加速度。

从 \(t\) 时刻开始，经过一小段时间 \(\Delta t\) 到达 \(t + \Delta t\) 时刻，使用欧拉方法（Euler Method），即假设在 $[t, t + \Delta t] $ 内角速度与线加速度保持不变，得到以下结果：
\[\begin{align} \mathbf{R}_{WB}(t+\Delta t) &= \mathbf{R}_{WB}(t) \text{Exp}(\mathbin{_B\pmb{\omega}_{WB}}(t)\Delta t) \ \mathbin{_W\mathbf{v}}(t+\Delta t) &= \mathbin{_W\mathbf{v}}(t) + \mathbin{_W\mathbf{a}}(t)\Delta t \ \mathbin{_W\mathbf{p}}(t+\Delta t) &= \mathbin{_W\mathbf{p}}(t) + \mathbin{_W\mathbf{v}}(t) \Delta t + \frac{1}{2}\mathbin{_W\mathbf{a}}(t)\Delta t^2 \end{align}\]
将公式 (\ref{eq2:imu_pre_mes_w}) (\ref{eq2:imu_pre_mes_a})，并忽略表示坐标系的下标，得到：
\[\begin{align} \mathbf{R}(t+\Delta t) &= \mathbf{R}(t) \text{Exp}((\tilde{\pmb{\omega}}(t) - \mathbf{b}^g(t) - \pmb{\eta}^{gd}(t))\Delta t) \label{eq2:imu_pre_delta_R} \ \mathbf{v}(t+\Delta t) &= \mathbf{v}(t) + \mathbf{g}\Delta t + \mathbf{R}(t)(\tilde{\mathbf{a}}(t) - \mathbf{b}^a(t) - \pmb{\eta}^{ad}(t))\Delta t \label{eq2:imu_pre_delta_v} \ \mathbf{p}(t+\Delta t) &= \mathbf{p}(t) + \mathbf{v}(t)\Delta t + \frac{1}{2}\mathbf{g}\Delta t^2 + \frac{1}{2}\mathbf{R}(t)(\tilde{\mathbf{a}}(t) - \mathbf{b}^a(t) - \pmb{\eta}^{ad}(t))\Delta t^2 \label{eq2:imu_pre_delta_p} \end{align}\]
其中上标 \(\cdot^{d}\) 表示离散（discrete），是在 \(\Delta t\) 时间段内的测量值的高斯误差。

从现在开始，考虑离散的情况。假设 \(\Delta t\) 是 IMU 测量值的时间间隔，从第 \(i\) 个 IMU 测量值积分到第 \(j\) 个 IMU 测量值，中间一共经历 \(j - i\) 个 \(\Delta t\) 时间段，按照公式 (\ref{eq2:imu_pre_delta_R}) (\ref{eq2:imu_pre_delta_v}) (\ref{eq2:imu_pre_delta_p})，可以从 \(i\) 时刻的状态值积分得到 \(j\) 时刻的状态值：
\[\begin{align} \mathbf{R}_j &= \mathbf{R}_i \prod_{k=i}^{j-1}\text{Exp}((\tilde{\pmb{\omega}}_k - \mathbf{b}^g_k - \pmb{\eta}^{gd}_k)\Delta t) \ \mathbf{v}_j &= \mathbf{v}_i + \mathbf{g}\Delta t_{ij} + \sum_{k=i}^{j-1}\mathbf{R}_k(\tilde{\mathbf{a}}_k - \mathbf{b}^a_k - \pmb{\eta}^{ad}_k)\Delta t\ \mathbf{p}_j &= \mathbf{p}_i + \sum_{k=i}^{j-1}\mathbf{v}_k\Delta t + \sum_{k=i}^{j-1}\frac{1}{2}\mathbf{g}\Delta t^2 + \frac{1}{2}\sum_{k=i}^{j-1}\mathbf{R}_k(\tilde{\mathbf{a}}_k - \mathbf{b}^a_k - \pmb{\eta}^{ad}_k)\Delta t^2 \end{align}\]
其中引入了新的变量 \(\Delta t_{ij} \doteq \sum_{k = i}^{j-1}\Delta t\)。接下来定义 \(i, j\) 时刻状态量之间的“差值”。按照“差值”的字面意思，可以直接写出 \(\mathbf{R}_i^T\mathbf{R}_j, \mathbf{v}_j - \mathbf{v}_i, \mathbf{p}_j - \mathbf{p}_i\)，然而这个太 NAIVE，这么写就不是预积分了。预积分定义的状态量如下：
\[\begin{align} \Delta \mathbf{R}_{ij} &\doteq \mathbf{R}_i^T \mathbf{R}_j = \prod_{k=i}^{j-1}\text{Exp}((\tilde{\pmb{\omega}}_k - \mathbf{b}^g_k - \pmb{\eta}^{gd}_k)\Delta t) \label{eq2:imu_pre_state_diff_delta_R_ij} \\Delta \mathbf{v}_{ij} &\doteq \mathbf{R}_i^T(\mathbf{v}_j - \mathbf{v}_i - \mathbf{g}\Delta t_{ij}) = \sum_{k=i}^{j-1}\Delta\mathbf{R}_{ik}(\tilde{\mathbf{a}}_k - \mathbf{b}^a_k - \pmb{\eta}^{ad}_k)\Delta t \label{eq2:imu_pre_state_diff_delta_v_ij} \\Delta \mathbf{p}_{ij} &\doteq \mathbf{R}_i^T(\mathbf{p}_j - \mathbf{p}_i - \mathbf{v}_i\Delta t_{ij} - \frac{1}{2}\mathbf{g}\Delta t_{ij}^2) \notag \&= \sum_{k=i}^{j-1}(\Delta\mathbf{v}_{ik}\Delta t + \frac{1}{2}\Delta\mathbf{R}_{ik}(\tilde{\mathbf{a}}_k - \mathbf{b}^a_k - \pmb{\eta}^{ad}_k)\Delta t) \notag \&= \sum_{k=i}^{j-1}\frac{3}{2}\Delta\mathbf{R}_{ik}(\tilde{\mathbf{a}}_k - \mathbf{b}^a_k - \pmb{\eta}^{ad}_k)\Delta t \label{eq2:imu_pre_state_diff_delta_p_ij} \end{align}\]
上面定义的状态量都与 \(i, j\) 时刻的状态量 \(\mathbf{R}_i, \mathbf{v}_i, \mathbf{p}_i, \mathbf{R}_j, \mathbf{v}_j, \mathbf{p}_j\) 无关。考虑到上面出现了中间时刻的角速度测量漂移值 \(\mathbf{b}^g_k\) 和线加速度测量漂移值 \(\mathbf{b}^a_k\)，为方便起见，假设 $\mathbf{b}^g_k = \mathbf{b}^g_i, \mathbf{b}^a_k = \mathbf{b}^a_i, k=i, i+1, \dots, j $。因为 Bias 也是需要估计出来的，这种假设减少大量需要估计的状态量。此处假设形成的近似，限制了 IMU 预积分的时间间隔，在应用的过程中应该注意到这一点。

下一步是将高斯误差与测量值、漂移值分隔开，以方便估计高斯误差。由 BCH 公式可得（这个地方还是值得推导一下的，第二个等号神复杂）：
\[\begin{align} \Delta\mathbf{R}_{ij} &\simeq \prod_{k=i}^{j-1} \left[ \text{Exp}((\tilde{\pmb{\omega}}_k - \mathbf{b}^g_i)\Delta t) \text{Exp}(-\mathbf{J}^k_r\pmb{\eta}^{gd}_k\Delta t) \right] \notag \ &= \Delta\tilde{\mathbf{R}}_{ij} \prod_{k=i}^{j-1} \text{Exp}(-\Delta\tilde{\mathbf{R}}^T_{k+1, j}\mathbf{J}^k_r\pmb{\eta}^{gd}_k\Delta t) \notag \ &\doteq \Delta\tilde{\mathbf{R}}_{ij} \text{Exp}(-\delta \pmb{\phi}_{ij}) \label{eq2:imu_pre_mes_state_diff_delta_R_ij} \end{align}\]
其中 \(\mathbf{J}^k_r\doteq\mathbf{J}^k_r(\tilde{\pmb{\omega}}_k - \mathbf{b}^g_i)\) 是 \(\mathfrak{so}(3)\) 的右雅可比。\(\Delta\tilde{\mathbf{R}}_{ij} \doteq \prod_{k=i}^{j-1}\exp((\tilde{\pmb{\omega}}_k - \mathbf{b}^g_i)\Delta t)\) 是 IMU 预积分的虚拟旋转测量值，\(\exp(-\delta \pmb{\phi}_{ij})\) 是对应的高斯误差。由此，可以进一步得到 IMU 预积分的虚拟速度和虚拟位移与它们的测量值、误差之间的关系：
\[\begin{align} \Delta\mathbf{v}_{ij} &\simeq \sum_{k=i}^{j-1} (\Delta\tilde{\mathbf{R}}_{ik}(\mathbf{I}-\delta\pmb{\phi}^{\wedge}_{ik})(\tilde{\mathbf{a}}_k-\mathbf{b}^a_i)\Delta t - \Delta\tilde{\mathbf{R}}_{ik}\pmb{\eta}^{ad}_k\Delta t) \notag \ &= \Delta\tilde{\mathbf{v}}_{ij} + \sum_{k=i}^{j-1} \left[\Delta\tilde{\mathbf{R}}_{ik}(\tilde{\mathbf{a}}_k-\mathbf{b}^a_i)^{\wedge}\delta\pmb{\phi}_{ik}\Delta t - \Delta\tilde{\mathbf{R}}_{ik}\pmb{\eta}^{ad}_k\Delta t \right] \notag \ &\doteq \Delta\tilde{\mathbf{v}}_{ij} - \delta\mathbf{v}_{ij} \label{eq2:imu_pre_mes_state_diff_delta_v_ij} \\Delta\mathbf{p}_{ij} &\simeq \sum_{k=i}^{j-1}\frac{3}{2}\Delta\tilde{\mathbf{R}}_{ik}(\mathbf{I}-\delta\pmb{\phi}^{\wedge}_{ik})(\tilde{\mathbf{a}}_k-\mathbf{b}^a_i)\Delta t^2 - \sum_{k=i}^{j-1}\frac{3}{2}\Delta\tilde{\mathbf{R}}_{ik}\pmb{\eta}^{ad}_k\Delta t^2 \notag \ &= \Delta\tilde{\mathbf{p}}_{ij} + \sum_{k=i}^{j-1}\left[\frac{3}{2}\Delta\tilde{\mathbf{R}}_{ik}(\tilde{\mathbf{a}}_k-\mathbf{b}^a_i)^{\wedge}\delta\pmb{\phi}_{ik}\Delta t^2 - \frac{3}{2}\Delta\tilde{\mathbf{R}}_{ik}\pmb{\eta}^{ad}_k\Delta t^2\right] \notag \ &\doteq \Delta\tilde{\mathbf{p}}_{ij} - \delta\mathbf{p}_{ij} \label{eq2:imu_pre_mes_state_diff_delta_p_ij} \end{align}\]

整理一下虚拟测量值与其误差:
\[\begin{align} \Delta\tilde{\mathbf{R}}_{ij} &\doteq \prod_{k=i}^{j-1}\text{Exp}((\tilde{\pmb{\omega}}_k - \mathbf{b}^g_i)\Delta t) \\text{Exp}(-\delta \pmb{\phi}_{ij}) &\doteq \prod_{k=i}^{j-1} \text{Exp}(-\Delta\tilde{\mathbf{R}}^T_{k+1, j}\mathbf{J}^k_r\pmb{\eta}^{gd}_k\Delta t) \label{eq2:imu_pre_mes_delta_phi_ij} \\Delta\tilde{\mathbf{v}}_{ij} &\doteq \sum_{k=i}^{j-1}\Delta\tilde{\mathbf{R}}_{ik}(\tilde{\mathbf{a}}_k-\mathbf{b}^a_i)\Delta t \-\delta \mathbf{v}_{ij} &\doteq \sum_{k=i}^{j-1} \left[\Delta\tilde{\mathbf{R}}_{ik}(\tilde{\mathbf{a}}_k-\mathbf{b}^a_i)^{\wedge}\delta\pmb{\phi}_{ik}\Delta t - \Delta\tilde{\mathbf{R}}_{ik}\pmb{\eta}^{ad}_k\Delta t \right] \label{eq2:imu_pre_mes_delta_v_ij} \\Delta\tilde{\mathbf{p}}_{ij} &\doteq \sum_{k=i}^{j-1}\frac{3}{2}\Delta\tilde{\mathbf{R}}_{ik}(\tilde{\mathbf{a}}_k-\mathbf{b}^a_i)\Delta t^2 \-\delta \mathbf{p}_{ij} &\doteq \sum_{k=i}^{j-1}\left[\frac{3}{2}\Delta\tilde{\mathbf{R}}_{ik}(\tilde{\mathbf{a}}_k-\mathbf{b}^a_i)^{\wedge}\delta\pmb{\phi}_{ik}\Delta t^2 - \frac{3}{2}\Delta\tilde{\mathbf{R}}_{ik}\pmb{\eta}^{ad}_k\Delta t^2\right] \label{eq2:imu_pre_mes_delta_p_ij} \\end{align} \]

将公式 (\ref{eq2:imu_pre_mes_state_diff_delta_R_ij}) (\ref{eq2:imu_pre_mes_state_diff_delta_v_ij}) (\ref{eq2:imu_pre_mes_state_diff_delta_p_ij})分别代入公式 (\ref{eq2:imu_pre_state_diff_delta_R_ij}) (\ref{eq2:imu_pre_state_diff_delta_v_ij}) (\ref{eq2:imu_pre_state_diff_delta_p_ij})，得到虚拟状态量测量值与 \(i, j\) 时刻状态量的联系:
\[\begin{align} \Delta\tilde{\mathbf{R}}_{ij} &= \mathbf{R}^T_i\mathbf{R}_j\text{Exp}(\delta\pmb{\phi}_{ij}) \ \Delta\tilde{\mathbf{v}}_{ij} &= \mathbf{R}^T_i(\mathbf{v}_j-\mathbf{v}_i-\mathbf{g}\Delta t_{ij}) + \delta\mathbf{v}_{ij} \ \Delta\tilde{\mathbf{p}}_{ij} &= \mathbf{R}^T_i(\mathbf{p}_j-\mathbf{p}_i-\mathbf{v}\Delta t_{ij}-\frac{1}{2}\mathbf{g}\Delta t^2_{ij}) + \delta \mathbf{p}_{ij} \end{align}\]
优化通过调整 \(i, j\) 时刻的状态量 \(\mathbf{R}_i, \mathbf{v}_i, \mathbf{p}_i, \mathbf{R}_j, \mathbf{v}_j, \mathbf{p}_j\)，最小化 \(\delta \pmb{\phi}_{ij}, \delta \mathbf{v}_{ij}, \delta \mathbf{p}_{ij}\)。

以上 \(\Delta\tilde{\mathbf{R}}_{ij}, \Delta\tilde{\mathbf{v}}_{ij}, \Delta\tilde{\mathbf{p}}_{ij}\) 虽然与 \(\mathbf{R}_i, \mathbf{v}_i, \mathbf{p}_i, \mathbf{R}_j, \mathbf{v}_j, \mathbf{p}_j\) 无关，但与 \(i\) 时刻的漂移值 \(\mathbf{b}^g_i, \mathbf{b}^a_i\) 相关，这两个漂移值也是需要估计的状态量，在优化过程中会发生改变，使得需要重新积分。为了解决这个问题，IMU 预积分使用泰勒展开进行近似。如果漂移值的变化量过大，则需要重新积分。在漂移值处的泰勒展开形式如下：

\[\begin{align} \Delta\tilde{\mathbf{R}}_{ij}(\mathbf{b}^g_i) &\simeq \Delta\tilde{\mathbf{R}}_{ij}(\bar{\mathbf{b}}^g_i)\text{Exp}\left(\frac{\partial\Delta\bar{\mathbf{R}}_{ij}}{\partial\mathbf{b}^g}\delta\mathbf{b}^g_i\right) \label{eq2:imu_pre_mes_update_bias_R} \ \Delta\tilde{\mathbf{v}}_{ij}(\mathbf{b}^g_i, \mathbf{b}^a_i) &\simeq \Delta\tilde{\mathbf{v}}_{ij}(\bar{\mathbf{b}}^g_i, \bar{\mathbf{b}}^a_i) + \frac{\partial\Delta\bar{\mathbf{v}}_{ij}}{\partial\mathbf{b}^g}\delta\mathbf{b}^g_i + \frac{\partial\Delta\bar{\mathbf{v}}_{ij}}{\partial\mathbf{b}^a}\delta\mathbf{b}^a_i \label{eq2:imu_pre_mes_update_bias_v} \ \Delta\tilde{\mathbf{p}}_{ij}(\mathbf{b}^g_i, \mathbf{b}^a_i) &\simeq \Delta\tilde{\mathbf{p}}_{ij}(\bar{\mathbf{b}}^g_i, \bar{\mathbf{b}}^a_i) + \frac{\partial\Delta\bar{\mathbf{p}}_{ij}}{\partial\mathbf{b}^g}\delta\mathbf{b}^g_i + \frac{\partial\Delta\bar{\mathbf{p}}_{ij}}{\partial\mathbf{b}^a}\delta\mathbf{b}^a_i \label{eq2:imu_pre_mes_update_bias_p} \end{align}\]

得到虚拟测量值的误差计算方法：

\[\begin{align} \mathbf{r}_{\Delta\mathbf{R}_{ij}} &\doteq -\delta \pmb{\phi}_{ij} = \text{Log}\left( \left( \Delta\tilde{\mathbf{R}}_{ij}(\bar{\mathbf{b}}^g_i) \text{Exp}\left( \frac{\partial\Delta\bar{\mathbf{R}}_{ij}}{\partial\mathbf{b}^g}\delta\mathbf{b}^g_i \right) \right)^T \mathbf{R}^T_i\mathbf{R}_j \right) \ \mathbf{r}_{\Delta\mathbf{v}_{ij}} &\doteq -\delta \mathbf{v}_{ij} = \mathbf{R}^T_i(\mathbf{v}_j - \mathbf{v}_i - \mathbf{g}\Delta t_{ij}) \notag \ &- \left( \Delta\tilde{\mathbf{v}}_{ij}(\bar{\mathbf{b}}^g_i, \bar{\mathbf{b}}^a_i) + \frac{\partial\Delta\bar{\mathbf{v}}_{ij}}{\partial\mathbf{b}^g}\delta\mathbf{b}^g_i + \frac{\partial\Delta\bar{\mathbf{v}}_{ij}}{\partial\mathbf{b}^a}\delta\mathbf{b}^a_i \right) \ \mathbf{r}_{\Delta\mathbf{p}_{ij}} &\doteq -\delta \mathbf{p}_{ij} = \mathbf{R}^T_i(\mathbf{p}_j-\mathbf{p}_i-\mathbf{v}\Delta t_{ij}-\frac{1}{2}\mathbf{g}\Delta t^2_{ij}) \notag \ &- \left( \Delta\tilde{\mathbf{p}}_{ij}(\bar{\mathbf{b}}^g_i, \bar{\mathbf{b}}^a_i) + \frac{\partial\Delta\bar{\mathbf{p}}_{ij}}{\partial\mathbf{b}^g}\delta\mathbf{b}^g_i + \frac{\partial\Delta\bar{\mathbf{p}}_{ij}}{\partial\mathbf{b}^a}\delta\mathbf{b}^a_i \right) \end{align}\]

Covariances

从 \(i\) 时刻到 \(j\) 时刻的积分使用了 \(j - i\) 组 IMU 测量值，这些测量值具有游走误差。这些误差的 covariance 需要累积，得到 IMU 预积分虚拟测量值的 covariance。

由公式 (\ref{eq2:imu_pre_mes_delta_phi_ij}) (\ref{eq2:imu_pre_mes_delta_v_ij}) (\ref{eq2:imu_pre_mes_delta_p_ij}) 可得：
\[\begin{align} \delta \pmb{\phi}_{ij} &= \sum_{k=i}^{j-1} \Delta\tilde{\mathbf{R}}^T_{k+1, j}\mathbf{J}^k_r\pmb{\eta}^{gd}_k\Delta t \\delta \mathbf{v}_{ij} &= \sum_{k=i}^{j-1} \left[-\Delta\tilde{\mathbf{R}}_{ik}(\tilde{\mathbf{a}}_k-\mathbf{b}^a_i)^{\wedge}\delta\pmb{\phi}_{ik}\Delta t + \Delta\tilde{\mathbf{R}}_{ik}\pmb{\eta}^{ad}_k\Delta t \right] \\delta \mathbf{p}_{ij} &\doteq \sum_{k=i}^{j-1}\left[-\frac{3}{2}\Delta\tilde{\mathbf{R}}_{ik}(\tilde{\mathbf{a}}_k-\mathbf{b}^a_i)^{\wedge}\delta\pmb{\phi}_{ik}\Delta t^2 + \frac{3}{2}\Delta\tilde{\mathbf{R}}_{ik}\pmb{\eta}^{ad}_k\Delta t^2\right] \end{align}\]

考虑 \(\delta \pmb{\phi}_{ij}, \delta \mathbf{v}_{ij}, \delta \mathbf{p}_{ij}\) 的迭代计算过程，即从 \(\delta \pmb{\phi}_{ik}, \delta \mathbf{v}_{ik}, \delta \mathbf{p}_{ik}\) 计算 \(\delta \pmb{\phi}_{i,k+1}, \delta \mathbf{v}_{i,k+1}, \delta \mathbf{p}_{i,k+1}\) 的过程。（注意，这里 \(\delta \mathbf{p}_{ij}\) 的推导结果与文章不同，确实无法认同文章。）

\[\begin{align} \delta \pmb{\phi}_{ij} &= \sum_{k=i}^{j-1} \Delta\tilde{\mathbf{R}}^T_{k+1, j}\mathbf{J}^k_r\pmb{\eta}^{gd}_k\Delta t \notag \\ &= \sum_{k=i}^{j-2} \Delta\tilde{\mathbf{R}}^T_{k+1, j}\mathbf{J}^k_r\pmb{\eta}^{gd}_k\Delta t + \Delta\tilde{\mathbf{R}}^T_{jj}\mathbf{J}^{j-1}_r\pmb{\eta}^{gd}_{j-1}\Delta t \notag \\ &= \sum_{k=i}^{j-2} (\Delta\tilde{\mathbf{R}}_{k+1, j-1}\Delta\tilde{\mathbf{R}}_{j-1, j})^T\mathbf{J}^k_r\pmb{\eta}^{gd}_k\Delta t + \mathbf{J}^{j-1}_r\pmb{\eta}^{gd}_{j-1}\Delta t \notag \\ &= \Delta\tilde{\mathbf{R}}_{j-1, j}^T\sum_{k=i}^{j-2} \Delta\tilde{\mathbf{R}}_{k+1, j-1}^T\mathbf{J}^k_r\pmb{\eta}^{gd}_k\Delta t + \mathbf{J}^{j-1}_r\pmb{\eta}^{gd}_{j-1}\Delta t \notag \\ &= \Delta\tilde{\mathbf{R}}_{j-1, j}^T \delta \pmb{\phi}_{i,j-1} + \mathbf{J}^{j-1}_r\pmb{\eta}^{gd}_{j-1}\Delta t \\ \delta \mathbf{v}_{ij} &= \sum_{k=i}^{j-1} \left[-\Delta\tilde{\mathbf{R}}_{ik}(\tilde{\mathbf{a}}_k-\mathbf{b}^a_i)^{\wedge}\delta\pmb{\phi}_{ik}\Delta t + \Delta\tilde{\mathbf{R}}_{ik}\pmb{\eta}^{ad}_k\Delta t \right] \notag \\ &= \sum_{k=i}^{j-2} \left[-\Delta\tilde{\mathbf{R}}_{ik}(\tilde{\mathbf{a}}_k-\mathbf{b}^a_i)^{\wedge}\delta\pmb{\phi}_{ik}\Delta t + \Delta\tilde{\mathbf{R}}_{ik}\pmb{\eta}^{ad}_k\Delta t \right] \notag \\ &-\Delta\tilde{\mathbf{R}}_{i,j-1}(\tilde{\mathbf{a}}_{j-1}-\mathbf{b}^a_i)^{\wedge}\delta\pmb{\phi}_{i,j-1}\Delta t + \Delta\tilde{\mathbf{R}}_{i,j-1}\pmb{\eta}^{ad}_{j-1}\Delta t \notag \\ &= \delta \mathbf{v}_{i,j-1} -\Delta\tilde{\mathbf{R}}_{i,j-1}(\tilde{\mathbf{a}}_{j-1}-\mathbf{b}^a_i)^{\wedge}\delta\pmb{\phi}_{i,j-1}\Delta t + \Delta\tilde{\mathbf{R}}_{i,j-1}\pmb{\eta}^{ad}_{j-1}\Delta t \\delta \mathbf{p}_{ij} &= \sum_{k=i}^{j-1}\left[-\frac{3}{2}\Delta\tilde{\mathbf{R}}_{ik}(\tilde{\mathbf{a}}_k-\mathbf{b}^a_i)^{\wedge}\delta\pmb{\phi}_{ik}\Delta t^2 + \frac{3}{2}\Delta\tilde{\mathbf{R}}_{ik}\pmb{\eta}^{ad}_k\Delta t^2\right] \notag \\ &= \sum_{k=i}^{j-2}\left[-\frac{3}{2}\Delta\tilde{\mathbf{R}}_{ik}(\tilde{\mathbf{a}}_k-\mathbf{b}^a_i)^{\wedge}\delta\pmb{\phi}_{ik}\Delta t^2 + \frac{3}{2}\Delta\tilde{\mathbf{R}}_{ik}\pmb{\eta}^{ad}_k\Delta t^2\right] \notag \\ &-\frac{3}{2}\Delta\tilde{\mathbf{R}}_{i,j-1}(\tilde{\mathbf{a}}_{j-1}-\mathbf{b}^a_i)^{\wedge}\delta\pmb{\phi}_{i,j-1}\Delta t^2 + \frac{3}{2}\Delta\tilde{\mathbf{R}}_{i,j-1}\pmb{\eta}^{ad}_{j-1}\Delta t^2 \notag \\ &= \delta \mathbf{p}_{i,j-1} -\frac{3}{2}\Delta\tilde{\mathbf{R}}_{i,j-1}(\tilde{\mathbf{a}}_{j-1}-\mathbf{b}^a_i)^{\wedge}\delta\pmb{\phi}_{i,j-1}\Delta t^2 + \frac{3}{2}\Delta\tilde{\mathbf{R}}_{i,j-1}\pmb{\eta}^{ad}_{j-1}\Delta t^2\end{align}\]

于是有：

\[\begin{align} \delta \pmb{\phi}_{i,k+1} &= \Delta\tilde{\mathbf{R}}_{k,k+1}^T \delta \pmb{\phi}_{ik} + \mathbf{J}^{k}_r\pmb{\eta}^{gd}_{k}\Delta t \\delta \mathbf{v}_{i,k+1} &= \delta \mathbf{v}_{i,k} -\Delta\tilde{\mathbf{R}}_{i,k}(\tilde{\mathbf{a}}_{k}-\mathbf{b}^a_i)^{\wedge}\delta\pmb{\phi}_{i,k}\Delta t + \Delta\tilde{\mathbf{R}}_{i,k}\pmb{\eta}^{ad}_{k}\Delta t \\delta \mathbf{p}_{i,k+1} &= \delta \mathbf{p}_{i,k} -\frac{3}{2}\Delta\tilde{\mathbf{R}}_{i,k}(\tilde{\mathbf{a}}_{k}-\mathbf{b}^a_i)^{\wedge}\delta\pmb{\phi}_{i,k}\Delta t^2 + \frac{3}{2}\Delta\tilde{\mathbf{R}}_{i,k}\pmb{\eta}^{ad}_{k}\Delta t^2 \end{align}\]

写成矩阵形式：

\[\begin{align} \begin{bmatrix} \delta \pmb{\phi}_{i,k+1} \\ \delta \mathbf{v}_{i,k+1} \\ \delta \mathbf{p}_{i,k+1} \end{bmatrix} &= \begin{bmatrix} \Delta\tilde{\mathbf{R}}_{k,k+1}^T & \mathbf{0}_{3\times3} & \mathbf{0}_{3\times3} \\ -\Delta\tilde{\mathbf{R}}_{i,k}(\tilde{\mathbf{a}}_{k}-\mathbf{b}^a_i)^{\wedge}\Delta t & \mathbf{I}_{3\times3} & \mathbf{0}_{3\times3} \\ -\frac{3}{2}\Delta\tilde{\mathbf{R}}_{i,k}(\tilde{\mathbf{a}}_{k}-\mathbf{b}^a_i)^{\wedge}\Delta t^2 & \mathbf{0}_{3\times3} & \mathbf{I}_{3\times3} \end{bmatrix} \begin{bmatrix} \delta \pmb{\phi}_{i,k} \\ \delta \mathbf{v}_{i,k} \\ \delta \mathbf{p}_{i,k} \end{bmatrix} \notag \\ &+ \begin{bmatrix} \mathbf{J}^{k}_r \Delta t & \mathbf{0}_{3\times3} \\ \mathbf{0}_{3\times3} & \Delta\tilde{\mathbf{R}}_{i,k} \Delta t \\ \mathbf{0}_{3\times3} & \frac{3}{2}\Delta\tilde{\mathbf{R}}_{i,k} \Delta t^2 \end{bmatrix} \begin{bmatrix} \pmb{\eta}^{gd}_{k} \\ \pmb{\eta}^{ad}_{k} \end{bmatrix} \end{align}\]

令

\[\begin{align} \mathbf{A} &= \begin{bmatrix} \Delta\tilde{\mathbf{R}}_{k,k+1}^T & \mathbf{0}_{3\times3} & \mathbf{0}_{3\times3} \\ -\Delta\tilde{\mathbf{R}}_{i,k}(\tilde{\mathbf{a}}_{k}-\mathbf{b}^a_i)^{\wedge}\Delta t & \mathbf{I}_{3\times3} & \mathbf{0}_{3\times3} \\ -\frac{3}{2}\Delta\tilde{\mathbf{R}}_{i,k}(\tilde{\mathbf{a}}_{k}-\mathbf{b}^a_i)^{\wedge}\Delta t^2 & \mathbf{0}_{3\times3} & \mathbf{I}_{3\times3} \end{bmatrix} \\mathbf{B} &= \begin{bmatrix} \mathbf{J}^{k}_r \Delta t & \mathbf{0}_{3\times3} \\ \mathbf{0}_{3\times3} & \Delta\tilde{\mathbf{R}}_{i,k} \Delta t \\ \mathbf{0}_{3\times3} & \frac{3}{2}\Delta\tilde{\mathbf{R}}_{i,k} \Delta t^2 \end{bmatrix} \end{align}\]

covariance propagation 的一步：
\[\begin{align} \pmb{\Sigma}_{i, k+1} = \mathbf{A} \pmb{\Sigma}_{i, k} \mathbf{A}^T + \mathbf{B} \pmb{\Sigma}_{\eta} \mathbf{B}^T \end{align}\]

Jacobians

Jacobians of Biases

计算公式 (\ref{eq2:imu_pre_mes_update_bias_R}) (\ref{eq2:imu_pre_mes_update_bias_v}) (\ref{eq2:imu_pre_mes_update_bias_p}) 中出现的 Jacobians，即 \(\frac{\partial\Delta\bar{\mathbf{R}}_{ij}}{\partial\mathbf{b}^g}, \frac{\partial\Delta\bar{\mathbf{v}}_{ij}}{\partial\mathbf{b}^g}, \frac{\partial\Delta\bar{\mathbf{v}}_{ij}}{\partial\mathbf{b}^a}, \frac{\partial\Delta\bar{\mathbf{p}}_{ij}}{\partial\mathbf{b}^g}, \frac{\partial\Delta\bar{\mathbf{p}}_{ij}}{\partial\mathbf{b}^a}\)。

更新 Bias ：\(\hat{\mathbf{b}}_i \leftarrow \bar{\mathbf{b}}_i + \delta \mathbf{b}_i\)。

\[\begin{align} \Delta\tilde{\mathbf{R}}_{ij}(\hat{\mathbf{b}}_i) &\doteq \prod_{k=i}^{j-1}\text{Exp}((\tilde{\pmb{\omega}}_k - \bar{\mathbf{b}}^g_i - \delta \mathbf{b}^g_i)\Delta t) \notag \\ &= \prod_{k=i}^{j-1}\left[\text{Exp}((\tilde{\pmb{\omega}}_k - \bar{\mathbf{b}}^g_i)\Delta t) \text{Exp}(- \mathbf{J}^k_r \delta \mathbf{b}^g_i \Delta t)\right] \notag \&= \prod_{k=i}^{j-1}\left[\text{Exp}(- \Delta\tilde{\mathbf{R}}_{k+1, j}(\bar{\mathbf{b}}_i^g)^T \mathbf{J}^k_r \delta \mathbf{b}^g_i \Delta t)\right] \notag \&= \Delta\tilde{\mathbf{R}}_{ij}(\bar{\mathbf{b}}_i) \text{Exp}(\sum_{k=i}^{j-1}\left[- \Delta\tilde{\mathbf{R}}_{k+1, j}(\bar{\mathbf{b}}_i^g)^T \mathbf{J}^k_r \Delta t\right] \delta \mathbf{b}^g_i) \notag \\ &= \Delta\tilde{\mathbf{R}}_{ij}(\bar{\mathbf{b}}_i)\text{Exp}\left(\frac{\partial\Delta\bar{\mathbf{R}}_{ij}}{\partial\mathbf{b}^g}\delta\mathbf{b}^g_i\right) \end{align}\]

上式中 \(\mathbf{J}^k_r = \mathbf{J}_r((\tilde{\pmb{\omega}}_k - \bar{\mathbf{b}}^g_i)\Delta t)\)。

\[\begin{align} \Delta\tilde{\mathbf{v}}_{ij}(\hat{\mathbf{b}}_i) &\doteq \sum_{k=i}^{j-1}\Delta\tilde{\mathbf{R}}_{ik}(\hat{\mathbf{b}}_i)(\tilde{\mathbf{a}}_k-\bar{\mathbf{b}}^a_i-\delta \mathbf{b}^a_i)\Delta t \notag \&= \sum_{k=i}^{j-1}\Delta\tilde{\mathbf{R}}_{ik}(\bar{\mathbf{b}}_i)\text{Exp}\left(\frac{\partial\Delta\bar{\mathbf{R}}_{ik}}{\partial\mathbf{b}^g}\delta\mathbf{b}^g_i\right)(\tilde{\mathbf{a}}_k-\bar{\mathbf{b}}^a_i-\delta \mathbf{b}^a_i)\Delta t \notag \&= \sum_{k=i}^{j-1}\Delta\tilde{\mathbf{R}}_{ik}(\bar{\mathbf{b}}_i)\left(\mathbf{I} + \left( \frac{\partial\Delta\bar{\mathbf{R}}_{ik}}{\partial\mathbf{b}^g}\delta\mathbf{b}^g_i \right)^{\wedge}\right)(\tilde{\mathbf{a}}_k-\bar{\mathbf{b}}^a_i-\delta \mathbf{b}^a_i)\Delta t \notag \\ &= \sum_{k=i}^{j-1}\Delta\tilde{\mathbf{R}}_{ik}(\bar{\mathbf{b}}_i)(\tilde{\mathbf{a}}_k-\bar{\mathbf{b}}^a_i)\Delta t + \sum_{k=i}^{j-1}\Delta\tilde{\mathbf{R}}_{ik}(\bar{\mathbf{b}}_i)(-\delta \mathbf{b}^a_i)\Delta t \notag \&+ \sum_{k=i}^{j-1}\Delta\tilde{\mathbf{R}}_{ik}(\bar{\mathbf{b}}_i)\left( \frac{\partial\Delta\bar{\mathbf{R}}_{ik}}{\partial\mathbf{b}^g}\delta\mathbf{b}^g_i \right)^{\wedge}(\tilde{\mathbf{a}}_k-\bar{\mathbf{b}}^a_i)\Delta t \notag \&= \sum_{k=i}^{j-1}\Delta\tilde{\mathbf{R}}_{ik}(\bar{\mathbf{b}}_i)(\tilde{\mathbf{a}}_k-\bar{\mathbf{b}}^a_i)\Delta t + \sum_{k=i}^{j-1}-\Delta\tilde{\mathbf{R}}_{ik}(\bar{\mathbf{b}}_i)\Delta t\delta \mathbf{b}^a_i \notag \&+ \sum_{k=i}^{j-1}-\Delta\tilde{\mathbf{R}}_{ik}(\bar{\mathbf{b}}_i)(\tilde{\mathbf{a}}_k-\bar{\mathbf{b}}^a_i)^{\wedge} \frac{\partial\Delta\bar{\mathbf{R}}_{ik}}{\partial\mathbf{b}^g}\Delta t\delta\mathbf{b}^g_i \notag \&= \Delta\tilde{\mathbf{v}}_{ij}(\bar{\mathbf{b}}_i) + \frac{\partial\Delta\bar{\mathbf{v}}_{ij}}{\partial\mathbf{b}^g}\delta\mathbf{b}^g_i + \frac{\partial\Delta\bar{\mathbf{v}}_{ij}}{\partial\mathbf{b}^a}\delta\mathbf{b}^a_i \end{align}\]

\[ \begin{align} \Delta\tilde{\mathbf{p}}_{ij}(\hat{\mathbf{b}}_i) &\doteq \sum_{k=i}^{j-1}\frac{3}{2}\Delta\tilde{\mathbf{R}}_{ik}(\hat{\mathbf{b}}_i)(\tilde{\mathbf{a}}_k-\bar{\mathbf{b}}^a_i-\delta \mathbf{b}^a_i)\Delta t^2 \notag \&= \sum_{k=i}^{j-1}\frac{3}{2}\Delta\tilde{\mathbf{R}}_{ik}(\bar{\mathbf{b}}_i)\text{Exp}\left(\frac{\partial\Delta\bar{\mathbf{R}}_{ik}}{\partial\mathbf{b}^g}\delta\mathbf{b}^g_i\right)(\tilde{\mathbf{a}}_k-\bar{\mathbf{b}}^a_i-\delta \mathbf{b}^a_i)\Delta t^2 \notag \&= \sum_{k=i}^{j-1}\frac{3}{2}\Delta\tilde{\mathbf{R}}_{ik}(\bar{\mathbf{b}}_i)\left( \mathbf{I} + \left(\frac{\partial\Delta\bar{\mathbf{R}}_{ik}}{\partial\mathbf{b}^g}\delta\mathbf{b}^g_i\right)^{\wedge} \right)(\tilde{\mathbf{a}}_k-\bar{\mathbf{b}}^a_i-\delta \mathbf{b}^a_i)\Delta t^2 \notag \&= \sum_{k=i}^{j-1}\frac{3}{2}\Delta\tilde{\mathbf{R}}_{ik}(\bar{\mathbf{b}}_i)(\tilde{\mathbf{a}}_k-\bar{\mathbf{b}}^a_i)\Delta t^2 + \sum_{k=i}^{j-1}-\frac{3}{2}\Delta\tilde{\mathbf{R}}_{ik}(\bar{\mathbf{b}}_i)\Delta t^2 \delta \mathbf{b}^a_i \notag \\ &+ \sum_{k=i}^{j-1}-\frac{3}{2}\Delta\tilde{\mathbf{R}}_{ik}(\bar{\mathbf{b}}_i)(\tilde{\mathbf{a}}_k-\bar{\mathbf{b}}^a_i)^{\wedge}\frac{\partial\Delta\bar{\mathbf{R}}_{ik}}{\partial\mathbf{b}^g}\Delta t^2 \delta\mathbf{b}^g_i \notag \&= \Delta\tilde{\mathbf{p}}_{ij}(\bar{\mathbf{b}}^g_i, \bar{\mathbf{b}}^a_i) + \frac{\partial\Delta\bar{\mathbf{p}}_{ij}}{\partial\mathbf{b}^g}\delta\mathbf{b}^g_i + \frac{\partial\Delta\bar{\mathbf{p}}_{ij}}{\partial\mathbf{b}^a}\delta\mathbf{b}^a_i \end{align} \]

综合以上：

\[\begin{align} \frac{\partial\Delta\bar{\mathbf{R}}_{ij}}{\partial\mathbf{b}^g} &= \sum_{k=i}^{j-1}\left[- \Delta\tilde{\mathbf{R}}_{k+1, j}(\bar{\mathbf{b}}_i^g)^T \mathbf{J}^k_r \Delta t\right] \notag \\ \frac{\partial\Delta\bar{\mathbf{v}}_{ij}}{\partial\mathbf{b}^g} &= \sum_{k=i}^{j-1}-\Delta\tilde{\mathbf{R}}_{ik}(\bar{\mathbf{b}}_i)(\tilde{\mathbf{a}}_k-\bar{\mathbf{b}}^a_i)^{\wedge} \frac{\partial\Delta\bar{\mathbf{R}}_{ik}}{\partial\mathbf{b}^g}\Delta t \notag \\ \frac{\partial\Delta\bar{\mathbf{v}}_{ij}}{\partial\mathbf{b}^a} &= \sum_{k=i}^{j-1}-\Delta\tilde{\mathbf{R}}_{ik}(\bar{\mathbf{b}}_i)\Delta t \notag \\ \frac{\partial\Delta\bar{\mathbf{p}}_{ij}}{\partial\mathbf{b}^g} &= \sum_{k=i}^{j-1}-\frac{3}{2}\Delta\tilde{\mathbf{R}}_{ik}(\bar{\mathbf{b}}_i)(\tilde{\mathbf{a}}_k-\bar{\mathbf{b}}^a_i)^{\wedge}\frac{\partial\Delta\bar{\mathbf{R}}_{ik}}{\partial\mathbf{b}^g}\Delta t^2 \notag \\frac{\partial\Delta\bar{\mathbf{p}}_{ij}}{\partial\mathbf{b}^a} &= \sum_{k=i}^{j-1}-\frac{3}{2}\Delta\tilde{\mathbf{R}}_{ik}(\bar{\mathbf{b}}_i)\Delta t^2 \end{align}\]

Jacobians of \(\mathbf{r}_{\Delta\mathbf{R}_{ij}}\)

\[\begin{align} \mathbf{r}_{\Delta\mathbf{R}_{ij}} &\doteq -\delta \pmb{\phi}_{ij} = \text{Log}\left( \left( \Delta\tilde{\mathbf{R}}_{ij}(\bar{\mathbf{b}}^g_i) \text{Exp}\left( \frac{\partial\Delta\bar{\mathbf{R}}_{ij}}{\partial\mathbf{b}^g}\delta\mathbf{b}^g_i \right) \right)^T \mathbf{R}^T_i\mathbf{R}_j \right) \end{align}\]

误差左乘或右乘，需要注意下面两个公式。这里按照 DSO 代码中误差左乘初始旋转矩阵，得到的结果如下。

\[\begin{align} &\mathbf{r}_{\Delta\mathbf{R}_{ij}} (\text{Exp}(\delta \pmb{\phi}_{i})\mathbf{R}_i) \notag \&= \text{Log}\left( \left( \Delta\tilde{\mathbf{R}}_{ij}(\bar{\mathbf{b}}^g_i) \text{Exp}\left( \frac{\partial\Delta\bar{\mathbf{R}}_{ij}}{\partial\mathbf{b}^g}\delta\mathbf{b}^g_i \right) \right)^T (\text{Exp}(\delta \pmb{\phi}_{i})\mathbf{R}_i)^T\mathbf{R}_j \right) \notag \&= \text{Log}\left( \left( \Delta\tilde{\mathbf{R}}_{ij}(\bar{\mathbf{b}}^g_i) \text{Exp}\left( \frac{\partial\Delta\bar{\mathbf{R}}_{ij}}{\partial\mathbf{b}^g}\delta\mathbf{b}^g_i \right) \right)^T \mathbf{R}_i^T \text{Exp}(-\delta \pmb{\phi}_{i}) \mathbf{R}_j \right) \notag \&= \text{Log}\left( \left( \Delta\tilde{\mathbf{R}}_{ij}(\bar{\mathbf{b}}^g_i) \text{Exp}\left( \frac{\partial\Delta\bar{\mathbf{R}}_{ij}}{\partial\mathbf{b}^g}\delta\mathbf{b}^g_i \right) \right)^T \mathbf{R}_i^T \mathbf{R}_j \mathbf{R}_j^T \text{Exp}(-\delta \pmb{\phi}_{i}) \mathbf{R}_j \right) \notag \\ &= \text{Log}\left( \left( \Delta\tilde{\mathbf{R}}_{ij}(\bar{\mathbf{b}}^g_i) \text{Exp}\left( \frac{\partial\Delta\bar{\mathbf{R}}_{ij}}{\partial\mathbf{b}^g}\delta\mathbf{b}^g_i \right) \right)^T \mathbf{R}_i^T \mathbf{R}_j \text{Exp}(-\mathbf{R}_j^T\delta \pmb{\phi}_{i}) \right) \notag \&= \text{Log}\left( \left( \Delta\tilde{\mathbf{R}}_{ij}(\bar{\mathbf{b}}^g_i) \text{Exp}\left( \frac{\partial\Delta\bar{\mathbf{R}}_{ij}}{\partial\mathbf{b}^g}\delta\mathbf{b}^g_i \right) \right)^T \mathbf{R}_i^T \mathbf{R}_j \right) \notag \\ &+ \mathbf{J}^{-1}_r\left(\text{Log}\left( \left( \Delta\tilde{\mathbf{R}}_{ij}(\bar{\mathbf{b}}^g_i) \text{Exp}\left( \frac{\partial\Delta\bar{\mathbf{R}}_{ij}}{\partial\mathbf{b}^g}\delta\mathbf{b}^g_i \right) \right)^T \mathbf{R}_i^T \mathbf{R}_j \right)\right)(-\mathbf{R}_j^T\delta \pmb{\phi}_{i}) \notag \&= \mathbf{r}_{\Delta\mathbf{R}_{ij}} (\mathbf{R}_i) - \mathbf{J}^{-1}_r (\mathbf{r}_{\Delta\mathbf{R}_{ij}} (\mathbf{R}_i))\mathbf{R}_j^T\delta \pmb{\phi}_{i}\end{align}\]

\[\begin{align} &\mathbf{r}_{\Delta\mathbf{R}_{ij}} (\text{Exp}(\delta \pmb{\phi}_{j})\mathbf{R}_j) \notag \\ &= \text{Log}\left( \left( \Delta\tilde{\mathbf{R}}_{ij}(\bar{\mathbf{b}}^g_i) \text{Exp}\left( \frac{\partial\Delta\bar{\mathbf{R}}_{ij}}{\partial\mathbf{b}^g}\delta\mathbf{b}^g_i \right) \right)^T \mathbf{R}_i^T \text{Exp}(\delta \pmb{\phi}_{j}) \mathbf{R}_j \right) \notag \\ &= \text{Log}\left( \left( \Delta\tilde{\mathbf{R}}_{ij}(\bar{\mathbf{b}}^g_i) \text{Exp}\left( \frac{\partial\Delta\bar{\mathbf{R}}_{ij}}{\partial\mathbf{b}^g}\delta\mathbf{b}^g_i \right) \right)^T \mathbf{R}_i^T \mathbf{R}_j \mathbf{R}_j^T \text{Exp}(\delta \pmb{\phi}_{j}) \mathbf{R}_j \right) \notag \\ &= \text{Log}\left( \left( \Delta\tilde{\mathbf{R}}_{ij}(\bar{\mathbf{b}}^g_i) \text{Exp}\left( \frac{\partial\Delta\bar{\mathbf{R}}_{ij}}{\partial\mathbf{b}^g}\delta\mathbf{b}^g_i \right) \right)^T \mathbf{R}_i^T \mathbf{R}_j \text{Exp}(\mathbf{R}_j^T \delta \pmb{\phi}_{j}) \right) \notag \&= \mathbf{r}_{\Delta\mathbf{R}_{ij}} (\mathbf{R}_j) + \mathbf{J}^{-1}_r(\mathbf{r}_{\Delta\mathbf{R}_{ij}} (\mathbf{R}_j)) \mathbf{R}_j^T \delta \pmb{\phi}_{j} \end{align}\]

Jacobians of \(\mathbf{r}_{\Delta\mathbf{v}_{ij}}\)

\[\begin{align} \mathbf{r}_{\Delta\mathbf{v}_{ij}} &\doteq -\delta \mathbf{v}_{ij} = \mathbf{R}^T_i(\mathbf{v}_j - \mathbf{v}_i - \mathbf{g}\Delta t_{ij}) \notag \ &- \left( \Delta\tilde{\mathbf{v}}_{ij}(\bar{\mathbf{b}}^g_i, \bar{\mathbf{b}}^a_i) + \frac{\partial\Delta\bar{\mathbf{v}}_{ij}}{\partial\mathbf{b}^g}\delta\mathbf{b}^g_i + \frac{\partial\Delta\bar{\mathbf{v}}_{ij}}{\partial\mathbf{b}^a}\delta\mathbf{b}^a_i \right) \end{align}\]

应当与论文中一致，待填。

Jacobians of \(\mathbf{r}_{\Delta\mathbf{p}_{ij}}\)

\[\begin{align} \mathbf{r}_{\Delta\mathbf{p}_{ij}} &\doteq -\delta \mathbf{p}_{ij} = \mathbf{R}^T_i(\mathbf{p}_j-\mathbf{p}_i-\mathbf{v}\Delta t_{ij}-\frac{1}{2}\mathbf{g}\Delta t^2_{ij}) \notag \ &- \left( \Delta\tilde{\mathbf{p}}_{ij}(\bar{\mathbf{b}}^g_i, \bar{\mathbf{b}}^a_i) + \frac{\partial\Delta\bar{\mathbf{p}}_{ij}}{\partial\mathbf{b}^g}\delta\mathbf{b}^g_i + \frac{\partial\Delta\bar{\mathbf{p}}_{ij}}{\partial\mathbf{b}^a}\delta\mathbf{b}^a_i \right) \end{align}\]

应当与论文中一致，待填。