洛谷 P8742题解

Posted 2023-05-21 xiayicheng

洛谷 P8742题解

简单版（P2347）传送门

原题传送门

有一道类似的题目（P2347），先扯一扯~

---

1.P2347

题目分析

动态规划入门题（01背包可行性问题）~

我们设 \\(dp_j\\) 为能否用砝码称出 \\(j\\) 重量，1 为可以，0 为不可以。

• 为了转移，\\(dp__0 \\gets 1\\)，什么都不放时，重量为 0，因此可以称出。

那么枚举 \\(dp__1 \\sim dp_sum(sum\\) 为砝码可称出的最大重量\\()\\)。

• 如果 \\(j-w\\) 可以称出，且重量为 \\(w\\) 的砝码存在、未超出个数限制，则 \\(j\\) 可以称出。即 \\(dp_j = dp_j - w(j - w \\geqslant 0)\\)

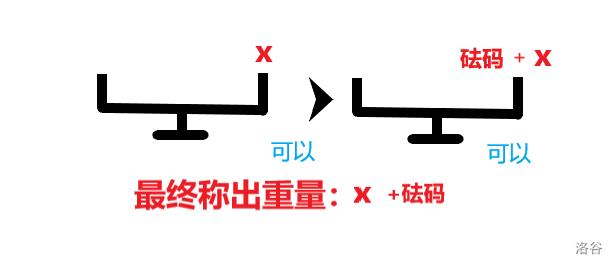
那么动态转移方程显而易见：

• \\(dp_j = dp_ j - a_i \\times k (j - a_i \\times k \\geqslant 0 , k \\leqslant b_i)\\)

PS：\\(a_i\\)：砝码 \\(i\\) 的重量，\\(b_i\\)：砝码 \\(i\\) 有的个数。

代码

#include<bits/stdc++.h>
using namespace std;
int n = 6, ans = 0, sum = 0;
int dp[1100], a[10] = 0, 1, 2, 3, 5, 10, 20, b[200];
int main()

	fill(dp, dp + 1100, 0);
	for (int i = 1; i <= n; i++) cin >> b[i], sum += a[i] * b[i];
	dp[0] = 1;
	for (int i = 1; i <= n; i++)
		for (int j = sum; j >= 0; j--) //反着来，不然会重复
			for (int k = 1; k <= b[i]; k++) 
				if (dp[j - a[i]*k] == 1 and j - a[i]*k >= 0 and dp[j] == 0)
					dp[j] = 1,ans++;
			
		
	

	cout << "Total=" << ans;
	return 0;

2.P8742

题目分析

因为砝码可以放另一边，即减去这个砝码的重量，所以反着还要再来遍历一遍。

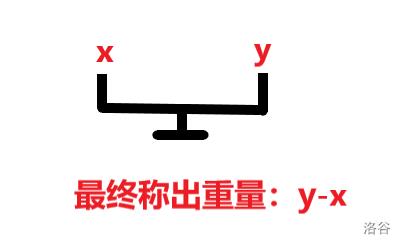
如果 \\(dp[j] + a[i] = 1\\) 那么 \\(dp[j] \\gets 1\\) 。

转移方程：

• \\(dp_j = dp_ j - a_i (j - a_i \\geqslant 0)\\)

• \\(dp_j = dp_ j + a_i (j + a_i \\leqslant sum)\\)

代码

#include <bits/stdc++.h>
using namespace std;
int dp[100010], a[110];
long long sum = 0, ans = 0;
int main()

	int n;
	cin >> n;
	fill(dp, dp + 100010, 0);
	dp[0] = 1;
	for (int i = 0; i < n; i++)
		cin >> a[i], sum += a[i];
	for (int i = 0; i < n; i++)
		for (int j = sum; j >= a[i]; j--) //优化，不枚举i<a[j]的情况
			if (dp[j - a[i]] == 1 and dp[j] != 1)
				dp[j] = 1, ans++;
		
	
	for (int i = 0; i < n; i++)
		for (int j = 1; j <= sum - a[i]; j++) //同理
			if (dp[j + a[i]] == 1 and dp[j] == 0)
					dp[j] = 1, ans++;
		
	
	cout << ans;
	return 0;

我的洛谷题解

• 2018.2.4 P1217【USACO1.5]回文质数 Prime Palindromes】
• 2018.2.6  P1308 【统计单词数】

链接

持续更新中