Number Reduction

Posted 2023-05-20 LIang2003

Number Reduction

题意

删除k位数，让原本的数变得最小（不含前导零）

思路

看官方题解学会的。记录每种数字出现的位置，原本有n位，那结果就有n-k位，一位位枚举，然后尽量放小的数，除了第一位不能放0，其他有0就放0。
为什么vector可以用得这么6啊

代码

void solve() 

	string x;
	cin>>x;
	cin>>k;
	//
	n=x.size();
	vector<vector<int>> pos(10);
	for(int i=0;i<n;i++) pos[x[i]-\'0\'].push_back(i);
	for(int i=0;i<10;i++) 
	
		reverse(pos[i].begin(),pos[i].end());
	
	string ans="";
	int last=0,len=n-k;
	for(int i=0;i<len;i++) 
	
		for(int d=(i==0);d<=9;d++) 
		
			while(!pos[d].empty()&&pos[d].back()<last) pos[d].pop_back();
			if(!pos[d].empty()&&pos[d].back()-last<=k)
			
				ans+=d+\'0\';
				k-=pos[d].back()-last;
				last=pos[d].back()+1;
				break;
			
		
	
	cout<<ans<<endl;

Dimensionality Reduction

Dimensionality Reduction 

--Hands-on Machine Learning with Scikit-Learn and TensorFlow -Chapter 8

---

Introduction 

 

1. 降维 pros：有助于加快训练速度；有助于数据可视化。cons：可能会导致重要信息丢失。
2. Two main approaches to dimensionality:projection and manifold learning 
3. Three popular dimensionality reduction techniques:PCA,Kernel PCA, and LLE

Two main approaches for Dimensionalty Reduction

1. Projection 在实际问题当中，训练数据通常是非均匀的分布在整个维度里面。有很多特征是连续的，但是有一些特征非常相似。结果这些训练数据在低纬度空间中挨得非常近。
2. Manifold Learning （流形学习）

---

 

PCA(Principal Component Analysis) 

1. pca是迄今为止最流行的降维算法。首先定义一个超平面，然后将数据投影到上面去。
2. pca降维应当注意点地方：
2.1 preserving the variance 

2.2 the axis minimizes the mean squared distance between the original dataset and projection onto the axis

       3.　Principal Components:PCA identifies the axis that accounts for the largest amount of variance in the training set.

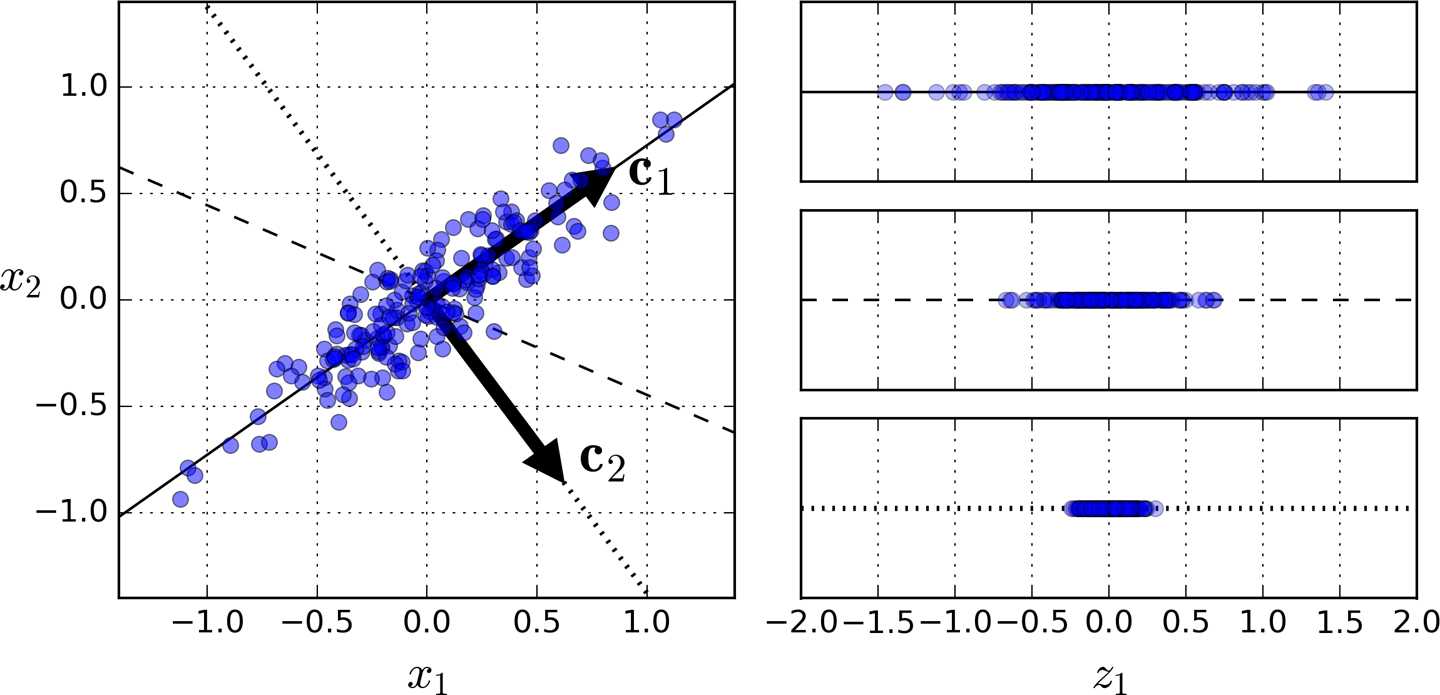
the unit vector that defines the i(th) axis is called i(th) principal component.

如何找到训练数据的主成分？Singular Value Decomposition(SVD)

 

PAC默认数据集是以愿数据为中心的。Sklearn 的pca 包已经将数据集中化处理了。而用其他方法构造pca时候，不要忘记首先集中化处理数据。（centering the data）

在降维的时候，一定要尽可能的保证更大的方差。

from sklearn.decomposition import PCA

pca=PCA(n_components=2)
X2D=pcd.fit_transform(X)
pca.explained_variance_ratio_

选择合适的维数