实验4 函数与异常处理编程
Posted zyj-
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了实验4 函数与异常处理编程相关的知识,希望对你有一定的参考价值。
实验任务1
源代码
print(sum) sum=42 print(sum) def inc(n): sum=n+1 print(sum) return sum sum=inc(7)+inc(7) print(sum)
运行截图

实验任务2
task2-1
源代码
def func1(a,b,c,d,e,f): return[a,b,c,d,e,f] def func2(a,b,c,*,d,e,f): return[a,b,c,d,e,f] def func3(a,b,c,/,d,e,f): return[a,b,c,d,e,f] print(func1(1,9,2,0,5,3)) print(func1(a=1,b=9,c=2,d=0,e=5,f=3)) print(func1(1,9,2,f=3,d=0,e=5)) print(func2(11,99,22,d=0,e=55,f=33)) print(func2(a=11,b=99,c=22,d=0,e=55,f=33)) print(func3(111,999,222,0,555,333)) print(func3(111,999,222,d=0,e=555,f=333))
运行截图

task2-2
源代码
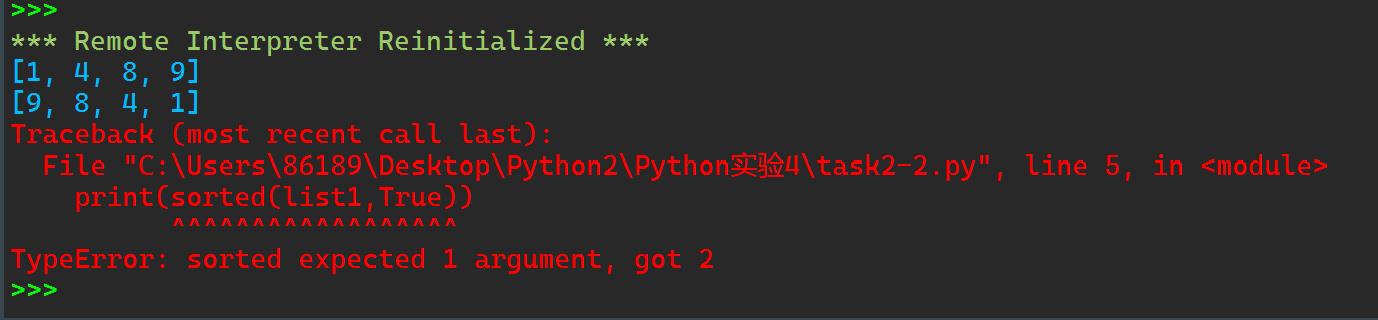
list1=[1,9,8,4] print(sorted(list1)) print(sorted(list1,reverse=True)) print(sorted(list1,True))
运行截图
task2-3
源代码
def func(a,b,c,/,*,d,e,f): return([a,b,c,d,e,f]) print(func(1,2,3,d=4,e=5,f=6))
运行截图

实验任务3
源代码
def solve(a,b,c): delta=b*b-4*a*c delta_sqrt=abs(delta)**0.5 p1=-b/2/a p2=delta_sqrt/2/a if delta>=0: root1=p1+p2 root2=p1-p2 else: root1=complex(p1,p2) root2=complex(p1,-p2) return root1,root2 print(solve.__doc__) while True: try: t=input(\'输入一元二次方程系数啊,吧,从,或者,输入#结束:\') if t==\'#\': print(\'结束运算,退出\') break a,b,c=map(float,t.split()) if a==0: raise ValueError(\'a=0,不是一元二次方程\') except ValueError as e: print(repr(e)) print() except: print(\'有其他错误发生\\n\') else: root1,root2=solve(a,b,c) print(f\'root1=root1:.2f,root2=root2:.2f\') print()
运行截图

实验任务4
源代码
def list_generator(a,b,c=1): if a==b: return a else: x=[] while a<=b: x.append(a) a+=c return x list1=list_generator(-5,5) print(list1) list2=list_generator(-5,5,2) print(list2) list3=list_generator(1,5,0.5) print(list3)
运行截图

实验任务5
源代码
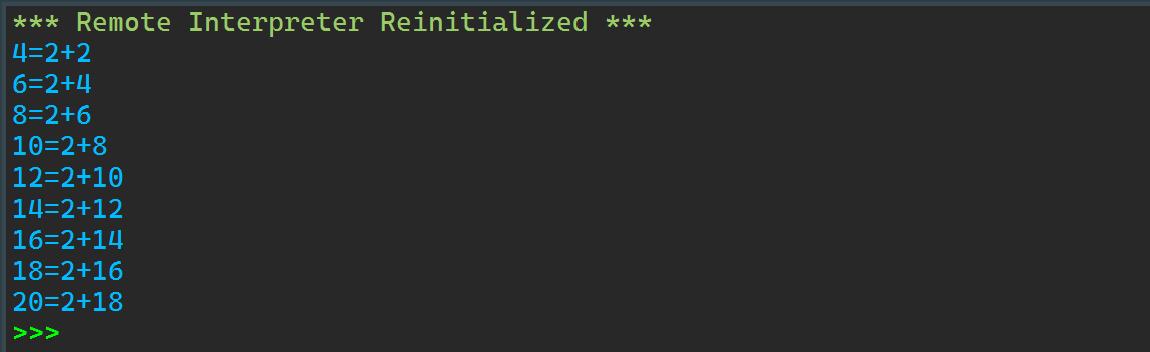
def is_prime(n): if n % 2==0: return True else: return False num=4 while num<=20: for i in range(2,num): if is_prime(i): if is_prime(num-i): print(f\'num=i+num-i\') break num+=2
运行截图
实验任务6
源代码
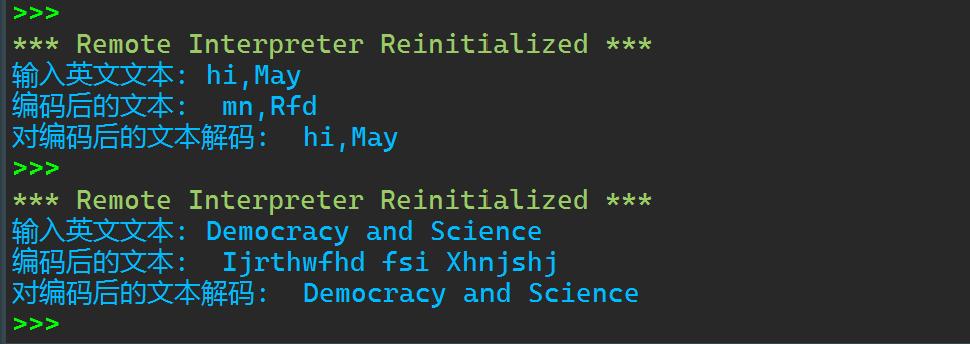
def encoder(text): text=list(text) i=0 while i <len(text): if text[i].isalpha(): if text[i].islower(): if ord(text[i])<=117: text[i]=chr(ord(text[i])+5) else: text[i]=chr(ord(text[i])+5-26) if text[i].isupper(): if ord(text[i])<=85: text[i]=chr(ord(text[i])+5) else: text[i]=chr(ord(text[i])+5-26) i+=1 return \'\'.join(text) def decoder(text): text=list(text) i=0 while i <len(text): if text[i].isalpha(): if text[i].islower(): if ord(text[i])>=102: text[i]=chr(ord(text[i])-5) else: text[i]=chr(ord(text[i])-5+26) if text[i].isupper(): if ord(text[i])>=46: text[i]=chr(ord(text[i])-5) else: text[i]=chr(ord(text[i])-5+26) i+=1 return \'\'.join(text) text = input(\'输入英文文本: \') encoded_text = encoder(text) print(\'编码后的文本: \', encoded_text) decoded_text = decoder(encoded_text) print(\'对编码后的文本解码: \', decoded_text)
运行截图
实验任务7
源代码
def collatz(n): if n%2==0: return n//2 else: return (n*3)+1 try: n=eval(input(\'Enter a positive integer:\')) if type(n) is float or type(n) is str or n<=0: raise ValueError(\'Error:must be a positive integer\') except ValueError as e: print(repr(e)) print() except: print(\'Error:must be a positive integer\') else: num=collatz(n) list=[n,num] while True: if num!=1: num=collatz(num) list.append(num) else: break print(list)
运行截图

实验任务8
源代码
def func(n): def func1(n): if n==0: return 1 else: return 2*func1(n-1) return func1(n)-1 while True: x = input() if x == \'#\': print(\'计算结束\') break n = int(x) ans = func(n) print(f\'n = n, ans = ans\')
运行截图

从函数式编程异常处理到薛定谔类型 -- 函数式编程本质(I)

首先说明一下
这里并不打算展开讲函数式异常处理
因为这篇文章的主题是介绍薛定谔类型.
关于前者我推荐medium上的一篇文章"Functional Error Handling".
本文很大程度上是受到这篇文章的启发
一句话来说
很多语言都有自己函数式处理异常的方式
也许你已经用过了
只是没有认识到这一点而已:
- Typescript的Union类型
- Swif的Option类型
- Haskell的Maybe类型
如果要给这种类型下个定义
那就是薛定谔类型(非公式说法)
怎么用薛定谔类型处理空指针异常?
这里用Typescript作为例子
如果一个函数没有处理Null会怎样:
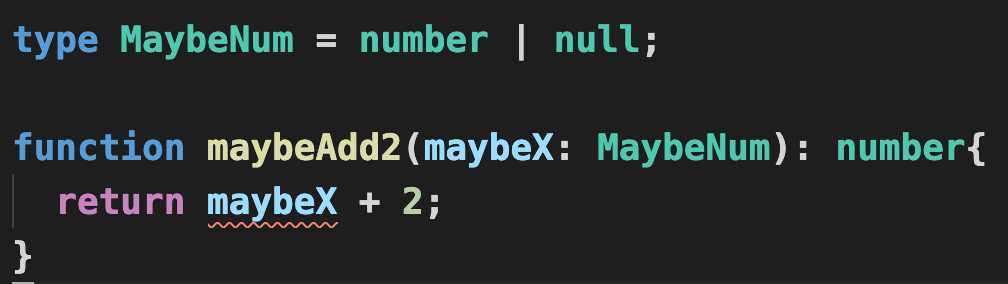
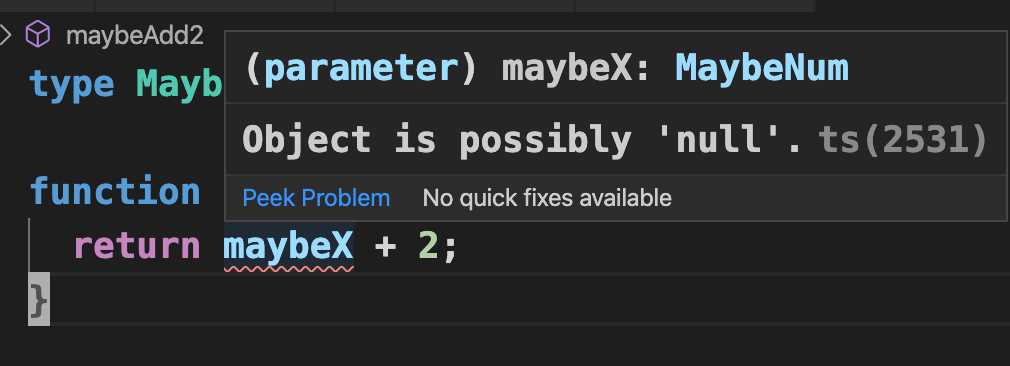
答案是编译器会报错
我们通过Union类型杜绝了出现空指针异常的可能性
从薛定谔类型异常处理看本质
从表象上看
我们通过编译器报错
回避了空指针异常
但是这个现象的本质是什么?
我会告诉你:
如果使用函数式编程, 且输入是合法的(排除非法数据导致异常的可能性,比如除以输入0),就能够回避所有的异常
你可能会说:这怎么可能?
但是这是事实
下面是推理过程:
- 函数式编程的函数是纯函数,对于任何合法输入,都有唯一确定的输出.
- 纯函数没有副作用,不会改变函数域外的变量(杜绝了绝大部分稀奇古怪的异常).
根据以上定义
将纯函数看作一个map
对于任意合法的key 都存在唯一一个对应value
所以请你告诉我y = map[key]这样一个简单的操作如何发生异常?
你会说:
要求输入合法是犯规啊!
现实中怎么能这样处理问题?
那么请你把纯函数看作一个数学函数y = f(x)
合法的key其实就是符合定义域的x
从这个角度去思考
你就不会纠结"合法key"这样一个定义了
可能你还会反驳
我在面向对象编程里
如果有合法输入也不会发生异常啊!
可是这是错的
无论你在函数里throw一个异常
或者是改一些全局变量
或者执行了一句"rm -rf /"
都有十足的可能发生异常
而纯函数杜绝了这些可能性.
纯函数通过消灭了可变性,回归数学,构造了一个绝对稳定,逻辑严谨的系统。
可是问题随之而来: 一个不变的系统,如何反应一个持续变化的客观世界?
也许这样说的太玄乎
举个例子:
在c语言里我用getChar()函数来获取用户的输入
先别纠结函数是不是写错了因为我也好久没用c了
这个操作本身是没有问题的
刚学写程序的人最熟悉这个
可是有人不乐意了
他们是函数式编程的推崇者
一群有洁癖的人(我不是在贬低他们,有洁癖的人最值得尊敬)
他们说:
getChar的输入永远为空
可是输出却有许多可能
这根本不是一个纯函数!
我们函数式编程不能容忍这种东西的存在!
所以问题就暴露了出来: 一个不变的系统,如何反应一个持续变化的客观世界(用户输入)?
如果有人告诉你是Monad
请你打断他的腿(Monad我会另找时间介绍, 我发现网上的说法很容易误导人)
真正的答案是薛定谔类型
薛定谔类型: 数学与现实世界的桥梁
在函数式世界里,我们用薛定谔类型表现一个持续变化的世界
如果以用户输入为例子
在Haskell里这个薛定谔类型就是IO
怎么理解IO呢?
我们可以认为它是一个所有用户输入的集合
但是在取出来之前
谁都不知道里面是什么
所以它是一个薛定谔类型
这里最重要的问题在于
纯函数是如何处理薛定谔类型的?
接下来我不用IO作为例子
因为我们通常用一个变量去接住这个输入,比如:
palindrome <- getLine
然后再用这个变量作为函数输入
这样一来函数就跟薛定谔类型(在这里就是IO)解耦了
起不到说明作用
我会以Maybe Num作为例子
假设一个有一个函数名叫maybeAdd2
接受一个MaybeNum类型作为输入
MaybeNum类型可能为null也可能为某个数字
下面是它的实现(原谅我用typescript作为例子):
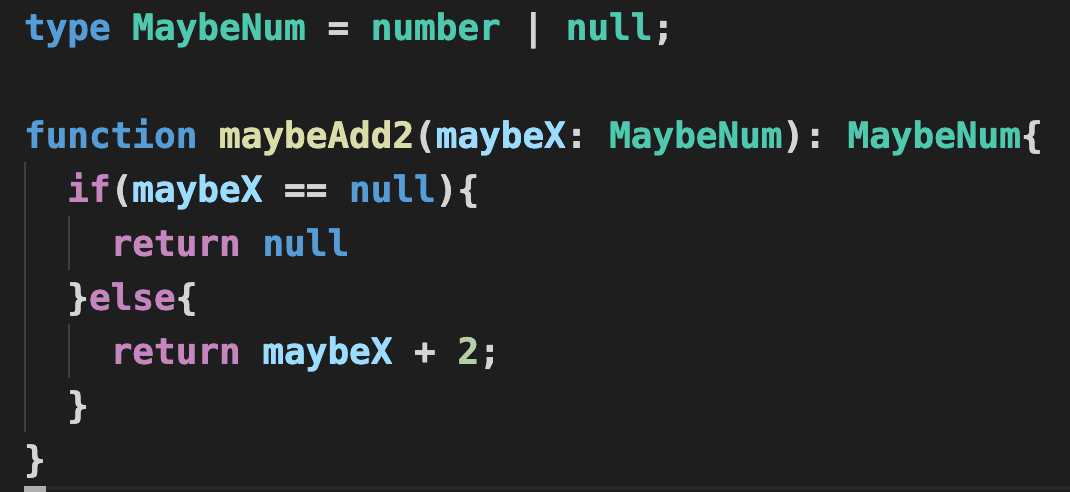
编译通过了
我们得到了一个处理薛定谔类型的函数!
这是非常了不起的
因为: 所有不确定的东西都可以用薛定谔类型表示
所以: 我们能处理现实世界的东西(We can deal with the f**king real world)
可是你可能会问: 这个真的是纯函数吗, 看起来不大像啊?
很好的问题
如果不符合纯函数
我们就又回到了交互式编程
函数式洁癖者也不会认同这种东西的存在
下面是推理:
输入maybe 2 => 输出maybe 4
输入maybe 3 => 输出maybe 5
输入maybe 4 => 输出maybe 6
...
好了这下你应该会同意这个函数是纯函数了.
下一篇文章我会谈谈Monad
也许这个系列就只有两篇文章
也许更多也说不定
我花了不少时间去码字
希望看完有帮助的能点个??
以上是关于实验4 函数与异常处理编程的主要内容,如果未能解决你的问题,请参考以下文章