数据挖掘实践（金融风控）：金融风控之贷款违约预测挑战赛（下篇）[xgboots/lightgbm/Catboost等模型]--模型融合：stackingblending

Posted 2023-05-17 ✨汀、

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了数据挖掘实践（金融风控）：金融风控之贷款违约预测挑战赛（下篇）[xgboots/lightgbm/Catboost等模型]--模型融合：stackingblending相关的知识，希望对你有一定的参考价值。

数据挖掘实践（金融风控）：金融风控之贷款违约预测挑战赛（下篇）[xgboots/lightgbm/Catboost等模型]--模型融合：stacking、blending

相关文章：数据挖掘实践（金融风控）：金融风控之贷款违约预测挑战赛(上篇)

数据挖掘机器学习专栏

4.建模与调参

项目链接以及码源见文末

4.1 模型对比与性能评估

4.1.1 逻辑回归

优点
- 训练速度较快，分类的时候，计算量仅仅只和特征的数目相关；
- 简单易理解，模型的可解释性非常好，从特征的权重可以看到不同的特征对最后结果的影响；
- 适合二分类问题，不需要缩放输入特征；
- 内存资源占用小，只需要存储各个维度的特征值；
缺点
- 逻辑回归需要预先处理缺失值和异常值【可参考task3特征工程】；
- 不能用Logistic回归去解决非线性问题，因为Logistic的决策面是线性的；
- 对多重共线性数据较为敏感，且很难处理数据不平衡的问题；
- 准确率并不是很高，因为形式非常简单，很难去拟合数据的真实分布；

4.1.2 决策树模型

优点
- 简单直观，生成的决策树可以可视化展示
- 数据不需要预处理，不需要归一化，不需要处理缺失数据
- 既可以处理离散值，也可以处理连续值
缺点
- 决策树算法非常容易过拟合，导致泛化能力不强（可进行适当的剪枝）
- 采用的是贪心算法，容易得到局部最优解

4.1.3 集成模型集成方法（ensemble method）

通过组合多个学习器来完成学习任务，通过集成方法，可以将多个弱学习器组合成一个强分类器，因此集成学习的泛化能力一般比单一分类器要好。

集成方法主要包括Bagging和Boosting，Bagging和Boosting都是将已有的分类或回归算法通过一定方式组合起来，形成一个更加强大的分类。两种方法都是把若干个分类器整合为一个分类器的方法，只是整合的方式不一样，最终得到不一样的效果。常见的基于Baggin思想的集成模型有：随机森林、基于Boosting思想的集成模型有：Adaboost、GBDT、XgBoost、LightGBM等。

Baggin和Boosting的区别总结如下：

样本选择上： Bagging方法的训练集是从原始集中有放回的选取，所以从原始集中选出的各轮训练集之间是独立的；而Boosting方法需要每一轮的训练集不变，只是训练集中每个样本在分类器中的权重发生变化。而权值是根据上一轮的分类结果进行调整
样例权重上： Bagging方法使用均匀取样，所以每个样本的权重相等；而Boosting方法根据错误率不断调整样本的权值，错误率越大则权重越大
预测函数上： Bagging方法中所有预测函数的权重相等；而Boosting方法中每个弱分类器都有相应的权重，对于分类误差小的分类器会有更大的权重
并行计算上： Bagging方法中各个预测函数可以并行生成；而Boosting方法各个预测函数只能顺序生成，因为后一个模型参数需要前一轮模型的结果。

4.1.4 模型评估方法

对于模型来说，其在训练集上面的误差我们称之为训练误差或者经验误差，而在测试集上的误差称之为测试误差。

对于我们来说，我们更关心的是模型对于新样本的学习能力，即我们希望通过对已有样本的学习，尽可能的将所有潜在样本的普遍规律学到手，而如果模型对训练样本学的太好，则有可能把训练样本自身所具有的一些特点当做所有潜在样本的普遍特点，这时候我们就会出现过拟合的问题。

因此我们通常将已有的数据集划分为训练集和测试集两部分，其中训练集用来训练模型，而测试集则是用来评估模型对于新样本的判别能力。

对于数据集的划分，我们通常要保证满足以下两个条件：

训练集和测试集的分布要与样本真实分布一致，即训练集和测试集都要保证是从样本真实分布中独立同分布采样而得；
训练集和测试集要互斥

对于数据集的划分有三种方法：留出法，交叉验证法和自助法，下面挨个介绍：

①留出法

留出法是直接将数据集D划分为两个互斥的集合，其中一个集合作为训练集S，另一个作为测试集T。需要注意的是在划分的时候要尽可能保证数据分布的一致性，即避免因数据划分过程引入额外的偏差而对最终结果产生影响。为了保证数据分布的一致性，通常我们采用分层采样的方式来对数据进行采样。

Tips： 通常，会将数据集D中大约2/3~4/5的样本作为训练集，其余的作为测试集。
②交叉验证法

k折交叉验证通常将数据集D分为k份，其中k-1份作为训练集，剩余的一份作为测试集，这样就可以获得k组训练/测试集，可以进行k次训练与测试，最终返回的是k个测试结果的均值。交叉验证中数据集的划分依然是依据分层采样的方式来进行。

对于交叉验证法，其k值的选取往往决定了评估结果的稳定性和保真性，通常k值选取10。

当k=1的时候，我们称之为留一法
③自助法

我们每次从数据集D中取一个样本作为训练集中的元素，然后把该样本放回，重复该行为m次，这样我们就可以得到大小为m的训练集，在这里面有的样本重复出现，有的样本则没有出现过，我们把那些没有出现过的样本作为测试集。

进行这样采样的原因是因为在D中约有36.8%的数据没有在训练集中出现过。留出法与交叉验证法都是使用分层采样的方式进行数据采样与划分，而自助法则是使用有放回重复采样的方式进行数据采样

数据集划分总结

对于数据量充足的时候，通常采用留出法或者k折交叉验证法来进行训练/测试集的划分；
对于数据集小且难以有效划分训练/测试集时使用自助法；
对于数据集小且可有效划分的时候最好使用留一法来进行划分，因为这种方法最为准确

4.1.5 模型评价标准

对于本次比赛，我们选用auc作为模型评价标准，类似的评价标准还有ks、f1-score等，具体介绍与实现大家可以回顾下task1中的内容。

一起来看一下auc到底是什么？

在逻辑回归里面，对于正负例的界定，通常会设一个阈值，大于阈值的为正类，小于阈值为负类。如果我们减小这个阀值，更多的样本会被识别为正类，提高正类的识别率，但同时也会使得更多的负类被错误识别为正类。为了直观表示这一现象，引入ROC。

根据分类结果计算得到ROC空间中相应的点，连接这些点就形成ROC curve，横坐标为False Positive Rate(FPR：假正率)，纵坐标为True Positive Rate(TPR：真正率)。一般情况下，这个曲线都应该处于(0,0)和(1,1)连线的上方,如图：

ROC曲线中的四个点：

点(0,1)：即FPR=0, TPR=1，意味着FN＝0且FP＝0，将所有的样本都正确分类；
点(1,0)：即FPR=1，TPR=0，最差分类器，避开了所有正确答案；
点(0,0)：即FPR=TPR=0，FP＝TP＝0，分类器把每个实例都预测为负类；
点(1,1)：分类器把每个实例都预测为正类

总之：ROC曲线越接近左上角，该分类器的性能越好，其泛化性能就越好。而且一般来说，如果ROC是光滑的，那么基本可以判断没有太大的overfitting。

但是对于两个模型，我们如何判断哪个模型的泛化性能更优呢？这里我们有主要以下两种方法：

如果模型A的ROC曲线完全包住了模型B的ROC曲线，那么我们就认为模型A要优于模型B；

如果两条曲线有交叉的话，我们就通过比较ROC与X，Y轴所围得曲线的面积来判断，面积越大，模型的性能就越优，这个面积我们称之为AUC(area under ROC curve)

4.2代码实战

import pandas as pd
import numpy as np
import warnings
import os
import seaborn as sns
import matplotlib.pyplot as plt
"""
sns 相关设置
@return:
"""
# 声明使用 Seaborn 样式
sns.set()
# 有五种seaborn的绘图风格，它们分别是：darkgrid, whitegrid, dark, white, ticks。默认的主题是darkgrid。
sns.set_style("whitegrid")
# 有四个预置的环境，按大小从小到大排列分别为：paper, notebook, talk, poster。其中，notebook是默认的。
sns.set_context(\'talk\')
# 中文字体设置-黑体
plt.rcParams[\'font.sans-serif\'] = [\'SimHei\']
# 解决保存图像是负号\'-\'显示为方块的问题
plt.rcParams[\'axes.unicode_minus\'] = False
# 解决Seaborn中文显示问题并调整字体大小
sns.set(font=\'SimHei\')

reduce_mem_usage 函数通过调整数据类型，帮助我们减少数据在内存中占用的空间

def reduce_mem_usage(df):
    start_mem = df.memory_usage().sum() 
    print(\'Memory usage of dataframe is :.2f MB\'.format(start_mem))
    
    for col in df.columns:
        col_type = df[col].dtype
        
        if col_type != object:
            c_min = df[col].min()
            c_max = df[col].max()
            if str(col_type)[:3] == \'int\':
                if c_min > np.iinfo(np.int8).min and c_max < np.iinfo(np.int8).max:
                    df[col] = df[col].astype(np.int8)
                elif c_min > np.iinfo(np.int16).min and c_max < np.iinfo(np.int16).max:
                    df[col] = df[col].astype(np.int16)
                elif c_min > np.iinfo(np.int32).min and c_max < np.iinfo(np.int32).max:
                    df[col] = df[col].astype(np.int32)
                elif c_min > np.iinfo(np.int64).min and c_max < np.iinfo(np.int64).max:
                    df[col] = df[col].astype(np.int64)  
            else:
                if c_min > np.finfo(np.float16).min and c_max < np.finfo(np.float16).max:
                    df[col] = df[col].astype(np.float16)
                elif c_min > np.finfo(np.float32).min and c_max < np.finfo(np.float32).max:
                    df[col] = df[col].astype(np.float32)
                else:
                    df[col] = df[col].astype(np.float64)
        else:
            df[col] = df[col].astype(\'category\')

    end_mem = df.memory_usage().sum() 
    print(\'Memory usage after optimization is: :.2f MB\'.format(end_mem))
    print(\'Decreased by :.1f%\'.format(100 * (start_mem - end_mem) / start_mem))
    
    return df

# 读取数据
data = pd.read_csv(\'dataset/data_for_model.csv\')
data = reduce_mem_usage(data)

Memory usage of dataframe is 928000128.00 MB
Memory usage after optimization is: 165006456.00 MB
Decreased by 82.2%

4.2.1 简单建模

Tips1：金融风控的实际项目多涉及到信用评分，因此需要模型特征具有较好的可解释性，所以目前在实际项目中多还是以逻辑回归作为基础模型。但是在比赛中以得分高低为准，不需要严谨的可解释性，所以大多基于集成算法进行建模。

Tips2：因为逻辑回归的算法特性，需要提前对异常值、缺失值数据进行处理【参考task3部分】

Tips3：基于树模型的算法特性，异常值、缺失值处理可以跳过，但是对于业务较为了解的同学也可以自己对缺失异常值进行处理，效果可能会更优于模型处理的结果。

注：以下建模的源数据参考baseline进行了相应的特征工程，对于异常缺失值未进行相应的处理操作。

建模之前的预操作

from sklearn.model_selection import KFold
# 分离数据集，方便进行交叉验证
X_train = data.loc[data[\'sample\']==\'train\', :].drop([\'id\',\'issueDate\',\'isDefault\', \'sample\'], axis=1)
X_test = data.loc[data[\'sample\']==\'test\', :].drop([\'id\',\'issueDate\',\'isDefault\', \'sample\'], axis=1)
y_train = data.loc[data[\'sample\']==\'train\', \'isDefault\']

# 5折交叉验证
folds = 5
seed = 2020
kf = KFold(n_splits=folds, shuffle=True, random_state=seed)

使用Lightgbm进行建模

"""对训练集数据进行划分，分成训练集和验证集，并进行相应的操作"""
from sklearn.model_selection import train_test_split
import lightgbm as lgb
# 数据集划分
X_train_split, X_val, y_train_split, y_val = train_test_split(X_train, y_train, test_size=0.2)
train_matrix = lgb.Dataset(X_train_split, label=y_train_split)
valid_matrix = lgb.Dataset(X_val, label=y_val)

params = 
            \'boosting_type\': \'gbdt\',
            \'objective\': \'binary\',
            \'learning_rate\': 0.1,
            \'metric\': \'auc\',
            \'min_child_weight\': 1e-3,
            \'num_leaves\': 31,
            \'max_depth\': -1,
            \'reg_lambda\': 0,
            \'reg_alpha\': 0,
            \'feature_fraction\': 1,
            \'bagging_fraction\': 1,
            \'bagging_freq\': 0,
            \'seed\': 2020,
            \'nthread\': 8,
            \'silent\': True,
            \'verbose\': -1,


"""使用训练集数据进行模型训练"""
model = lgb.train(params, train_set=train_matrix, valid_sets=valid_matrix, num_boost_round=20000, verbose_eval=1000, early_stopping_rounds=200)

Training until validation scores don\'t improve for 200 rounds
Early stopping, best iteration is:
[427]	valid_0\'s auc: 0.724947

对验证集进行预测

from sklearn import metrics
from sklearn.metrics import roc_auc_score

"""预测并计算roc的相关指标"""
val_pre_lgb = model.predict(X_val, num_iteration=model.best_iteration)
fpr, tpr, threshold = metrics.roc_curve(y_val, val_pre_lgb)
roc_auc = metrics.auc(fpr, tpr)
print(\'未调参前lightgbm单模型在验证集上的AUC：\'.format(roc_auc))
"""画出roc曲线图"""
plt.figure(figsize=(8, 8))
plt.title(\'Validation ROC\')
plt.plot(fpr, tpr, \'b\', label = \'Val AUC = %0.4f\' % roc_auc)
plt.ylim(0,1)
plt.xlim(0,1)
plt.legend(loc=\'best\')
plt.title(\'ROC\')
plt.ylabel(\'True Positive Rate\')
plt.xlabel(\'False Positive Rate\')
# 画出对角线
plt.plot([0,1],[0,1],\'r--\')
plt.show()

未调参前lightgbm单模型在验证集上的AUC：0.7249469360631181

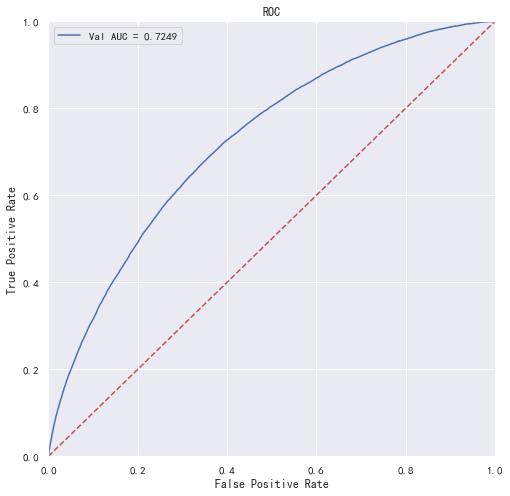
更进一步的，使用5折交叉验证进行模型性能评估

import lightgbm as lgb
"""使用lightgbm 5折交叉验证进行建模预测"""
cv_scores = []
for i, (train_index, valid_index) in enumerate(kf.split(X_train, y_train)):
    print(\'************************************  ************************************\'.format(str(i+1)))
    X_train_split, y_train_split, X_val, y_val = X_train.iloc[train_index], y_train[train_index], X_train.iloc[valid_index], y_train[valid_index]
    
    train_matrix = lgb.Dataset(X_train_split, label=y_train_split)
    valid_matrix = lgb.Dataset(X_val, label=y_val)

    params = 
                \'boosting_type\': \'gbdt\',
                \'objective\': \'binary\',
                \'learning_rate\': 0.1,
                \'metric\': \'auc\',
        
                \'min_child_weight\': 1e-3,
                \'num_leaves\': 31,
                \'max_depth\': -1,
                \'reg_lambda\': 0,
                \'reg_alpha\': 0,
                \'feature_fraction\': 1,
                \'bagging_fraction\': 1,
                \'bagging_freq\': 0,
                \'seed\': 2020,
                \'nthread\': 8,
                \'silent\': True,
                \'verbose\': -1,
    
    
    model = lgb.train(params, train_set=train_matrix, num_boost_round=20000, valid_sets=valid_matrix, verbose_eval=1000, early_stopping_rounds=200)
    val_pred = model.predict(X_val, num_iteration=model.best_iteration)
    
    cv_scores.append(roc_auc_score(y_val, val_pred))
    print(cv_scores)

print("lgb_scotrainre_list:".format(cv_scores))
print("lgb_score_mean:".format(np.mean(cv_scores)))
print("lgb_score_std:".format(np.std(cv_scores)))

...
lgb_scotrainre_list:[0.7303837315833632, 0.7258692125145638, 0.7305149209921737, 0.7296117869375041, 0.7294438695369077]
lgb_score_mean:0.7291647043129024
lgb_score_std:0.0016998349834934656

4.2.2 模型调参（贪心、网格搜索、贝叶斯）

贪心调参

先使用当前对模型影响最大的参数进行调优，达到当前参数下的模型最优化，再使用对模型影响次之的参数进行调优，如此下去，直到所有的参数调整完毕。

这个方法的缺点就是可能会调到局部最优而不是全局最优，但是只需要一步一步的进行参数最优化调试即可，容易理解。

需要注意的是在树模型中参数调整的顺序，也就是各个参数对模型的影响程度，这里列举一下日常调参过程中常用的参数和调参顺序：

①：max_depth、num_leaves
②：min_data_in_leaf、min_child_weight
③：bagging_fraction、 feature_fraction、bagging_freq
④：reg_lambda、reg_alpha
⑤：min_split_gain

from sklearn.model_selection import cross_val_score

# 调objective
best_obj = dict()
for obj in objective:
    model = LGBMRegressor(objective=obj)
    """预测并计算roc的相关指标"""
    score = cross_val_score(model, X_train, y_train, cv=5, scoring=\'roc_auc\').mean()
    best_obj[obj] = score
    
# num_leaves
best_leaves = dict()
for leaves in num_leaves:
    model = LGBMRegressor(objective=min(best_obj.items(), key=lambda x:x[1])[0], num_leaves=leaves)
    """预测并计算roc的相关指标"""
    score = cross_val_score(model, X_train, y_train, cv=5, scoring=\'roc_auc\').mean()
    best_leaves[leaves] = score
    
# max_depth
best_depth = dict()
for depth in max_depth:
    model = LGBMRegressor(objective=min(best_obj.items(), key=lambda x:x[1])[0],
                          num_leaves=min(best_leaves.items(), key=lambda x:x[1])[0],
                          max_depth=depth)
    """预测并计算roc的相关指标"""
    score = cross_val_score(model, X_train, y_train, cv=5, scoring=\'roc_auc\').mean()
    best_depth[depth] = score

"""
可依次将模型的参数通过上面的方式进行调整优化，并且通过可视化观察在每一个最优参数下模型的得分情况
"""

可依次将模型的参数通过上面的方式进行调整优化，并且通过可视化观察在每一个最优参数下模型的得分情况

网格搜索

sklearn 提供GridSearchCV用于进行网格搜索，只需要把模型的参数输进去，就能给出最优化的结果和参数。相比起贪心调参，网格搜索的结果会更优，但是网格搜索只适合于小数据集，一旦数据的量级上去了，很难得出结果。

同样以Lightgbm算法为例，进行网格搜索调参：

"""通过网格搜索确定最优参数"""
from sklearn.model_selection import GridSearchCV

def get_best_cv_params(learning_rate=0.1, n_estimators=581, num_leaves=31, max_depth=-1, bagging_fraction=1.0, 
                       feature_fraction=1.0, bagging_freq=0, min_data_in_leaf=20, min_child_weight=0.001, 
                       min_split_gain=0, reg_lambda=0, reg_alpha=0, param_grid=None):
    # 设置5折交叉验证
    cv_fold = StratifiedKFold(n_splits=5, random_state=0, shuffle=True, )
    
    model_lgb = lgb.LGBMClassifier(learning_rate=learning_rate,
                                   n_estimators=n_estimators,
                                   num_leaves=num_leaves,
                                   max_depth=max_depth,
                                   bagging_fraction=bagging_fraction,
                                   feature_fraction=feature_fraction,
                                   bagging_freq=bagging_freq,
                                   min_data_in_leaf=min_data_in_leaf,
                                   min_child_weight=min_child_weight,
                                   min_split_gain=min_split_gain,
                                   reg_lambda=reg_lambda,
                                   reg_alpha=reg_alpha,
                                   n_jobs= 8
                                  )
    grid_search = GridSearchCV(estimator=model_lgb, 
                               cv=cv_fold,
                               param_grid=param_grid,
                               scoring=\'roc_auc\'
                              )
    grid_search.fit(X_train, y_train)

    print(\'模型当前最优参数为:\'.format(grid_search.best_params_))
    print(\'模型当前最优得分为:\'.format(grid_search.best_score_))

"""以下代码未运行，耗时较长，请谨慎运行，且每一步的最优参数需要在下一步进行手动更新，请注意"""

"""
需要注意一下的是，除了获取上面的获取num_boost_round时候用的是原生的lightgbm（因为要用自带的cv）
下面配合GridSearchCV时必须使用sklearn接口的lightgbm。
"""
"""设置n_estimators 为581，调整num_leaves和max_depth，这里选择先粗调再细调"""
lgb_params = \'num_leaves\': range(10, 80, 5), \'max_depth\': range(3,10,2)
get_best_cv_params(learning_rate=0.1, n_estimators=581, num_leaves=None, max_depth=None, min_data_in_leaf=20, 
                   min_child_weight=0.001,bagging_fraction=1.0, feature_fraction=1.0, bagging_freq=0, 
                   min_split_gain=0, reg_lambda=0, reg_alpha=0, param_grid=lgb_params)

"""num_leaves为30，max_depth为7，进一步细调num_leaves和max_depth"""
lgb_params = \'num_leaves\': range(25, 35, 1), \'max_depth\': range(5,9,1)
get_best_cv_params(learning_rate=0.1, n_estimators=85, num_leaves=None, max_depth=None, min_data_in_leaf=20, 
                   min_child_weight=0.001,bagging_fraction=1.0, feature_fraction=1.0, bagging_freq=0, 
                   min_split_gain=0, reg_lambda=0, reg_alpha=0, param_grid=lgb_params)

"""
确定min_data_in_leaf为45，min_child_weight为0.001 ，下面进行bagging_fraction、feature_fraction和bagging_freq的调参
"""
lgb_params = \'bagging_fraction\': [i/10 for i in range(5,10,1)], 
              \'feature_fraction\': [i/10 for i in range(5,10,1)],
              \'bagging_freq\': range(0,81,10)
             
get_best_cv_params(learning_rate=0.1, n_estimators=85, num_leaves=29, max_depth=7, min_data_in_leaf=45, 
                   min_child_weight=0.001,bagging_fraction=None, feature_fraction=None, bagging_freq=None, 
                   min_split_gain=0, reg_lambda=0, reg_alpha=0, param_grid=lgb_params)

"""
确定bagging_fraction为0.4、feature_fraction为0.6、bagging_freq为 ，下面进行reg_lambda、reg_alpha的调参
"""
lgb_params = \'reg_lambda\': [0,0.001,0.01,0.03,0.08,0.3,0.5], \'reg_alpha\': [0,0.001,0.01,0.03,0.08,0.3,0.5]
get_best_cv_params(learning_rate=0.1, n_estimators=85, num_leaves=29, max_depth=7, min_data_in_leaf=45, 
                   min_child_weight=0.001,bagging_fraction=0.9, feature_fraction=0.9, bagging_freq=40, 
                   min_split_gain=0, reg_lambda=None, reg_alpha=None, param_grid=lgb_params)

"""
确定reg_lambda、reg_alpha都为0，下面进行min_split_gain的调参
"""
lgb_params = \'min_split_gain\': [i/10 for i in range(0,11,1)]
get_best_cv_params(learning_rate=0.1, n_estimators=85, num_leaves=29, max_depth=7, min_data_in_leaf=45, 
                   min_child_weight=0.001,bagging_fraction=0.9, feature_fraction=0.9, bagging_freq=40, 
                   min_split_gain=None, reg_lambda=0, reg_alpha=0, param_grid=lgb_params)

"""
参数确定好了以后，我们设置一个比较小的learning_rate 0.005，来确定最终的num_boost_round
"""
# 设置5折交叉验证
# cv_fold = StratifiedKFold(n_splits=5, random_state=0, shuffle=True, )
final_params = 
                \'boosting_type\': \'gbdt\',
                \'learning_rate\': 0.01,
                \'num_leaves\': 29,
                \'max_depth\': 7,
                \'min_data_in_leaf\':45,
                \'min_child_weight\':0.001,
                \'bagging_fraction\': 0.9,
                \'feature_fraction\': 0.9,
                \'bagging_freq\': 40,
                \'min_split_gain\': 0,
                \'reg_lambda\':0,
                \'reg_alpha\':0,
                \'nthread\': 6
               

cv_result = lgb.cv(train_set=lgb_train,
                   early_stopping_rounds=20,
                   num_boost_round=5000,
                   nfold=5,
                   stratified=True,
                   shuffle=True,
                   params=final_params,
                   metrics=\'auc\',
                   seed=0,
                  )

print(\'迭代次数\'.format(len(cv_result[\'auc-mean\'])))
print(\'交叉验证的AUC为\'.format(max(cv_result[\'auc-mean\'])))

在实际调整过程中，可先设置一个较大的学习率（上面的例子中0.1），通过Lgb原生的cv函数进行树个数的确定，之后再通过上面的实例代码进行参数的调整优化。

最后针对最优的参数设置一个较小的学习率（例如0.05），同样通过cv函数确定树的个数，确定最终的参数。

需要注意的是，针对大数据集，上面每一层参数的调整都需要耗费较长时间，

贝叶斯调参

在使用之前需要先安装包bayesian-optimization，运行如下命令即可：

pip install bayesian-optimization

贝叶斯调参的主要思想是：给定优化的目标函数(广义的函数，只需指定输入和输出即可，无需知道内部结构以及数学性质)，通过不断地添加样本点来更新目标函数的后验分布(高斯过程,直到后验分布基本贴合于真实分布）。简单的说，就是考虑了上一次参数的信息，从而更好的调整当前的参数。

贝叶斯调参的步骤如下：

定义优化函数(rf_cv）
建立模型
定义待优化的参数
得到优化结果，并返回要优化的分数指标

from sklearn.model_selection import cross_val_score

"""定义优化函数"""
def rf_cv_lgb(num_leaves, max_depth, bagging_fraction, feature_fraction, bagging_freq, min_data_in_leaf, 
              min_child_weight, min_split_gain, reg_lambda, reg_alpha):
    # 建立模型
    model_lgb = lgb.LGBMClassifier(boosting_type=\'gbdt\', bjective=\'binary\', metric=\'auc\',
                                   learning_rate=0.1, n_estimators=5000,
                                   num_leaves=int(num_leaves), max_depth=int(max_depth), 
                                   bagging_fraction=round(bagging_fraction, 2), feature_fraction=round(feature_fraction, 2),
                                   bagging_freq=int(bagging_freq), min_data_in_leaf=int(min_data_in_leaf),
                                   min_child_weight=min_child_weight, min_split_gain=min_split_gain,
                                   reg_lambda=reg_lambda, reg_alpha=reg_alpha,
                                   n_jobs= 8
                                  )
    
    val = cross_val_score(model_lgb, X_train_split, y_train_split, cv=5, scoring=\'roc_auc\').mean()
    
    return val

from bayes_opt import BayesianOptimization
"""定义优化参数"""
bayes_lgb = BayesianOptimization(
    rf_cv_lgb, 
    
        \'num_leaves\':(10, 200),
        \'max_depth\':(3, 20),
        \'bagging_fraction\':(0.5, 1.0),
        \'feature_fraction\':(0.5, 1.0),
        \'bagging_freq\':(0, 100),
        \'min_data_in_leaf\':(10,100),
        \'min_child_weight\':(0, 10),
        \'min_split_gain\':(0.0, 1.0),
        \'reg_alpha\':(0.0, 10),
        \'reg_lambda\':(0.0, 10),
    
)

"""开始优化"""
bayes_lgb.maximize(n_iter=10)

|   iter    |  target   | baggin... | baggin... | featur... | max_depth | min_ch... | min_da... | min_sp... | num_le... | reg_alpha | reg_la... |
-------------------------------------------------------------------------------------------------------------------------------------------------
| [0m 1       [0m | [0m 0.7263  [0m | [0m 0.7196  [0m | [0m 80.73   [0m | [0m 0.7988  [0m | [0m 19.17   [0m | [0m 5.751   [0m | [0m 40.71   [0m | [0m 0.9548  [0m | [0m 176.2   [0m | [0m 2.939   [0m | [0m 7.212   [0m |
| [95m 2       [0m | [95m 0.7279  [0m | [95m 0.8997  [0m | [95m 74.72   [0m | [95m 0.5904  [0m | [95m 7.259   [0m | [95m 6.175   [0m | [95m 92.03   [0m | [95m 0.4027  [0m | [95m 51.65   [0m | [95m 6.404   [0m | [95m 4.781   [0m |
| [0m 3       [0m | [0m 0.7207  [0m | [0m 0.5133  [0m | [0m 16.53   [0m | [0m 0.9536  [0m | [0m 4.974   [0m | [0m 2.37    [0m | [0m 98.08   [0m | [0m 0.7909  [0m | [0m 52.12   [0m | [0m 4.443   [0m | [0m 4.429   [0m |
| [0m 4       [0m | [0m 0.7276  [0m | [0m 0.6265  [0m | [0m 53.12   [0m | [0m 0.7307  [0m | [0m 10.67   [0m | [0m 1.824   [0m | [0m 18.98   [0m | [0m 0.954   [0m | [0m 60.47   [0m | [0m 6.963   [0m | [0m 1.999   [0m |
| [0m 5       [0m | [0m 0.6963  [0m | [0m 0.6509  [0m | [0m 11.58   [0m | [0m 0.5386  [0m | [0m 11.21   [0m | [0m 7.85    [0m | [0m 11.4    [0m | [0m 0.4269  [0m | [0m 153.0   [0m | [0m 0.5227  [0m | [0m 2.257   [0m |
| [0m 6       [0m | [0m 0.7276  [0m | [0m 0.6241  [0m | [0m 49.76   [0m | [0m 0.6057  [0m | [0m 10.34   [0m | [0m 1.718   [0m | [0m 22.43   [0m | [0m 0.8294  [0m | [0m 55.68   [0m | [0m 6.759   [0m | [0m 2.6     [0m |
| [95m 7       [0m | [95m 0.7283  [0m | [95m 0.9815  [0m | [95m 96.15   [0m | [95m 0.6961  [0m | [95m 19.45   [0m | [95m 1.627   [0m | [95m 37.7    [0m | [95m 0.4185  [0m | [95m 14.22   [0m | [95m 7.057   [0m | [95m 9.924   [0m |
| [0m 8       [0m | [0m 0.7278  [0m | [0m 0.7139  [0m | [0m 96.83   [0m | [0m 0.5063  [0m | [0m 3.941   [0m | [0m 1.469   [0m | [0m 97.28   [0m | [0m 0.07553 [0m | [0m 196.9   [0m | [0m 7.988   [0m | [0m 2.159   [0m |
| [0m 9       [0m | [0m 0.7195  [0m | [0m 0.5352  [0m | [0m 98.72   [0m | [0m 0.9699  [0m | [0m 4.445   [0m | [0m 1.767   [0m | [0m 13.91   [0m | [0m 0.1647  [0m | [0m 191.5   [0m | [0m 4.003   [0m | [0m 2.027   [0m |
| [0m 10      [0m | [0m 0.7281  [0m | [0m 0.7281  [0m | [0m 73.63   [0m | [0m 0.5598  [0m | [0m 19.29   [0m | [0m 0.5344  [0m | [0m 99.66   [0m | [0m 0.933   [0m | [0m 101.4   [0m | [0m 8.836   [0m | [0m 0.9222  [0m |
| [0m 11      [0m | [0m 0.7279  [0m | [0m 0.8213  [0m | [0m 0.05856 [0m | [0m 0.7626  [0m | [0m 17.49   [0m | [0m 8.447   [0m | [0m 10.71   [0m | [0m 0.3252  [0m | [0m 13.64   [0m | [0m 9.319   [0m | [0m 0.4747  [0m |
| [0m 12      [0m | [0m 0.7281  [0m | [0m 0.8372  [0m | [0m 95.71   [0m | [0m 0.9598  [0m | [0m 10.32   [0m | [0m 8.394   [0m | [0m 15.23   [0m | [0m 0.4909  [0m | [0m 94.48   [0m | [0m 9.486   [0m | [0m 9.044   [0m |
| [0m 13      [0m | [0m 0.6993  [0m | [0m 0.5183  [0m | [0m 99.02   [0m | [0m 0.542   [0m | [0m 15.5    [0m | [0m 8.35    [0m | [0m 38.15   [0m | [0m 0.4079  [0m | [0m 58.01   [0m | [0m 0.2668  [0m | [0m 1.652   [0m |
| [0m 14      [0m | [0m 0.7267  [0m | [0m 0.7933  [0m | [0m 4.459   [0m | [0m 0.79    [0m | [0m 7.557   [0m | [0m 2.43    [0m | [0m 27.91   [0m | [0m 0.8725  [0m | [0m 28.32   [0m | [0m 9.967   [0m | [0m 9.885   [0m |
| [0m 15      [0m | [0m 0.6979  [0m | [0m 0.9419  [0m | [0m 1.22    [0m | [0m 0.835   [0m | [0m 11.56   [0m | [0m 9.962   [0m | [0m 93.79   [0m | [0m 0.018   [0m | [0m 197.6   [0m | [0m 9.711   [0m | [0m 3.78    [0m |
=================================================================================================================================================

"""显示优化结果"""
bayes_lgb.max

\'target\': 0.7282530196283977,
 \'params\': \'bagging_fraction\': 0.9815471914843896,
  \'bagging_freq\': 96.14757648686668,
  \'feature_fraction\': 0.6961281791730929,
  \'max_depth\': 19.45450235568963,
  \'min_child_weight\': 1.6266132496156782,
  \'min_data_in_leaf\': 37.697878831472295,
  \'min_split_gain\': 0.4184947943942168,
  \'num_leaves\': 14.221122487200399,
  \'reg_alpha\': 7.056502173310882,
  \'reg_lambda\': 9.924023764203156

参数优化完成后，我们可以根据优化后的参数建立新的模型，降低学习率并寻找最优模型迭代次数

"""调整一个较小的学习率，并通过cv函数确定当前最优的迭代次数"""
base_params_lgb = 
                    \'boosting_type\': \'gbdt\',
                    \'objective\': \'binary\',
                    \'metric\': \'auc\',
                    \'learning_rate\': 0.01,
                    \'num_leaves\': 14,
                    \'max_depth\': 19,
                    \'min_data_in_leaf\': 37,
                    \'min_child_weight\':1.6,
                    \'bagging_fraction\': 0.98,
                    \'feature_fraction\': 0.69,
                    \'bagging_freq\': 96,
                    \'reg_lambda\': 9,
                    \'reg_alpha\': 7,
                    \'min_split_gain\': 0.4,
                    \'nthread\': 8,
                    \'seed\': 2020,
                    \'silent\': True,
                    \'verbose\': -1,


cv_result_lgb = lgb.cv(
    train_set=train_matrix,
    early_stopping_rounds=1000, 
    num_boost_round=20000,
    nfold=5,
    stratified=True,
    shuffle=True,
    params=base_params_lgb,
    metrics=\'auc\',
    seed=0
)

print(\'迭代次数\'.format(len(cv_result_lgb[\'auc-mean\'])))
print(\'最终模型的AUC为\'.format(max(cv_result_lgb[\'auc-mean\'])))

迭代次数14269
最终模型的AUC为0.7315032037635779

模型参数已经确定，建立最终模型并对验证集进行验证

import lightgbm as lgb
"""使用lightgbm 5折交叉验证进行建模预测"""
cv_scores = []
for i, (train_index, valid_index) in enumerate(kf.split(X_train, y_train)):
    print(\'************************************  ************************************\'.format(str(i+1)))
    X_train_split, y_train_split, X_val, y_val = X_train.iloc[train_index], y_train[train_index], X_train.iloc[valid_index], y_train[valid_index]
    
    train_matrix = lgb.Dataset(X_train_split, label=y_train_split)
    valid_matrix = lgb.Dataset(X_val, label=y_val)

    params = 
                \'boosting_type\': \'gbdt\',
                \'objective\': \'binary\',
                \'metric\': \'auc\',
                \'learning_rate\': 0.01,
                \'num_leaves\': 14,
                \'max_depth\': 19,
                \'min_data_in_leaf\': 37,
                \'min_child_weight\':1.6,
                \'bagging_fraction\': 0.98,
                \'feature_fraction\': 0.69,
                \'bagging_freq\': 96,
                \'reg_lambda\': 9,
                \'reg_alpha\': 7,
                \'min_split_gain\': 0.4,
                \'nthread\': 8,
                \'seed\': 2020,
                \'silent\': True,
    
    
    model = lgb.train(params, train_set=train_matrix, num_boost_round=14269, valid_sets=valid_matrix, verbose_eval=1000, early_stopping_rounds=200)
    val_pred = model.predict(X_val, num_iteration=model.best_iteration)
    
    cv_scores.append(roc_auc_score(y_val, val_pred))
    print(cv_scores)

print("lgb_scotrainre_list:".format(cv_scores))
print("lgb_score_mean:".format(np.mean(cv_scores)))
print("lgb_score_std:".format(np.std(cv_scores)))

...
lgb_scotrainre_list:[0.7329726464187137, 0.7294292852806246, 0.7341505801564857, 0.7328331383185244, 0.7317405262608612]
lgb_score_mean:0.732225235287042
lgb_score_std:0.0015929470575114753

通过5折交叉验证可以发现，模型迭代次数在13000次的时候会停之，那么我们在建立新模型时直接设置最大迭代次数，并使用验证集进行模型预测

""""""
base_params_lgb = 
                    \'boosting_type\': \'gbdt\',
                    \'objective\': \'binary\',
                    \'metric\': \'auc\',
                    \'learning_rate\': 0.01,
                    \'num_leaves\': 14,
                    \'max_depth\': 19,
                    \'min_data_in_leaf\': 37,
                    \'min_child_weight\':1.6,
                    \'bagging_fraction\': 0.98,
                    \'feature_fraction\': 0.69,
                    \'bagging_freq\': 96,
                    \'reg_lambda\': 9,
                    \'reg_alpha\': 7,
                    \'min_split_gain\': 0.4,
                    \'nthread\': 8,
                    \'seed\': 2020,
                    \'silent\': True,


"""使用训练集数据进行模型训练"""
final_model_lgb = lgb.train(base_params_lgb, train_set=train_matrix, valid_sets=valid_matrix, num_boost_round=13000, verbose_eval=1000, early_stopping_rounds=200)

"""预测并计算roc的相关指标"""
val_pre_lgb = final_model_lgb.predict(X_val)
fpr, tpr, threshold = metrics.roc_curve(y_val, val_pre_lgb)
roc_auc = metrics.auc(fpr, tpr)
print(\'调参后lightgbm单模型在验证集上的AUC：\'.format(roc_auc))
"""画出roc曲线图"""
plt.figure(figsize=(8, 8))
plt.title(\'Validation ROC\')
plt.plot(fpr, tpr, \'b\', label = \'Val AUC = %0.4f\' % roc_auc)
plt.ylim(0,1)
plt.xlim(0,1)
plt.legend(loc=\'best\')
plt.title(\'ROC\')
plt.ylabel(\'True Positive Rate\')
plt.xlabel(\'False Positive Rate\')
# 画出对角线
plt.plot([0,1],[0,1],\'r--\')
plt.show()

Training until validation scores don\'t improve for 200 rounds
[1000]	valid_0\'s auc: 0.723676
[2000]	valid_0\'s auc: 0.727282
[3000]	valid_0\'s auc: 0.728593
[4000]	valid_0\'s auc: 0.729493
[5000]	valid_0\'s auc: 0.730087
[6000]	valid_0\'s auc: 0.730515
[7000]	valid_0\'s auc: 0.730872
[8000]	valid_0\'s auc: 0.731121
[9000]	valid_0\'s auc: 0.731351
[10000]	valid_0\'s auc: 0.731502
[11000]	valid_0\'s auc: 0.731707
Early stopping, best iteration is:
[11192]	valid_0\'s auc: 0.731741
调参后lightgbm单模型在验证集上的AUC：0.7317405262608612

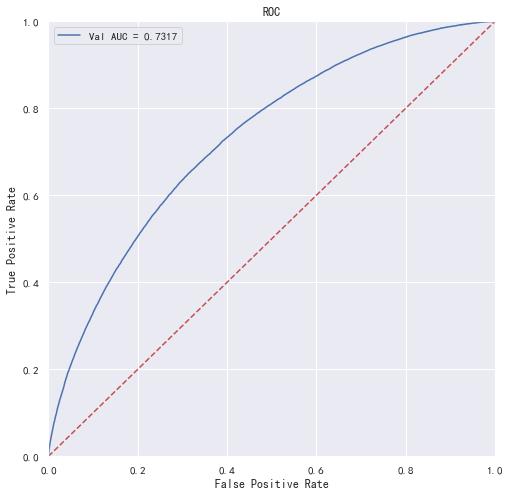
可以看到相比最早的原始参数，模型的性能还是有提升的

"""保存模型到本地"""
# 保存模型
import pickle
pickle.dump(final_model_lgb, open(\'dataset/model_lgb_best.pkl\', \'wb\'))

4.3 模型调参小总结**

集成模型内置的cv函数可以较快的进行单一参数的调节，一般可以用来优先确定树模型的迭代次数
数据量较大的时候（例如本次项目的数据），网格搜索调参会特别特别慢，不建议尝试
集成模型中原生库和sklearn下的库部分参数不一致，需要注意，具体可以参考xgb和lgb的官方API

xgb原生库API，sklearn库下xgbAPI

lgb原生库API， sklearn库下lgbAPI

4.4 模型相关原理介绍

由于相关算法原理篇幅较长，本文推荐了一些博客与教材供初学者们进行学习。

5.模型融合

5.1 stacking\\blending详解

stacking
将若干基学习器获得的预测结果，将预测结果作为新的训练集来训练一个学习器。如下图假设有五个基学习器，将数据带入五基学习器中得到预测结果，再带入模型六中进行训练预测。但是由于直接由五个基学习器获得结果直接带入模型六中，容易导致过拟合。所以在使用五个及模型进行预测的时候，可以考虑使用K折验证，防止过拟合。

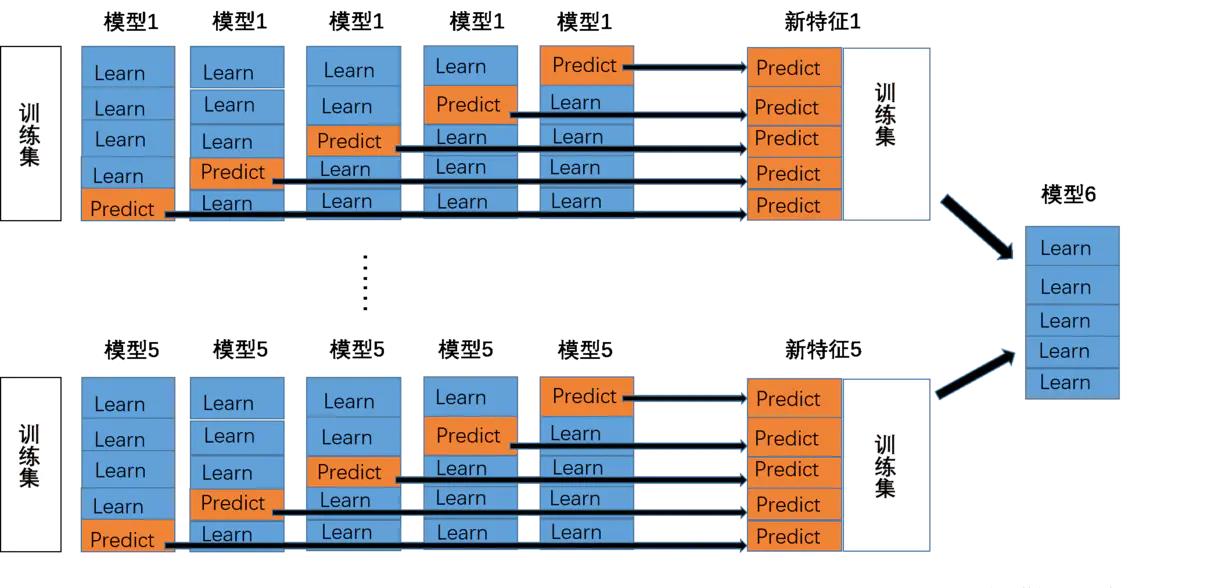
blending
与stacking不同，blending是将预测的值作为新的特征和原特征合并，构成新的特征值，用于预测。为了防止过拟合，将数据分为两部分d1、d2，使用d1的数据作为训练集，d2数据作为测试集。预测得到的数据作为新特征使用d2的数据作为训练集结合新特征，预测测试集结果。

Blending与stacking的不同
- stacking
  - stacking中由于两层使用的数据不同，所以可以避免信息泄露的问题。
  - 在组队竞赛的过程中，不需要给队友分享自己的随机种子。
- Blending
  - 由于blending对将数据划分为两个部分，在最后预测时有部分数据信息将被忽略。
  - 同时在使用第二层数据时可能会因为第二层数据较少产生过拟合现象。

参考资料：还是没有理解透彻吗？可以查看参考资料进一步了解哦!
https://blog.csdn.net/wuzhongqiang/article/details/105012739

5.1.1 平均：

简单加权平均，结果直接融合
求多个预测结果的平均值。pre1-pren分别是n组模型预测出来的结果，将其进行加权融

pre = (pre1 + pre2 + pre3 +...+pren )/n

加权平均法
一般根据之前预测模型的准确率，进行加权融合，将准确性高的模型赋予更高的权重。

pre = 0.3pre1 + 0.3pre2 + 0.4pre3

5.1.2 投票

简单投票

from xgboost import XGBClassifier
from sklearn.linear_model import LogisticRegression
from sklearn.ensemble import RandomForestClassifier, VotingClassifier
clf1 = LogisticRegression(random_state=1)
clf2 = RandomForestClassifier(random_state=1)
clf3 = XGBClassifier(learning_rate=0.1, n_estimators=150, max_depth=4, min_child_weight=2, subsample=0.7,objective=\'binary:logistic\')
 
vclf = VotingClassifier(estimators=[(\'lr\', clf1), (\'rf\', clf2), (\'xgb\', clf3)])
vclf = vclf .fit(x_train,y_train)
print(vclf .predict(x_test))

- 加权投票
在VotingClassifier中加入参数 voting=\'soft\', weights=[2, 1, 1]，weights用于调节基模型的权重

from xgboost import XGBClassifier
from sklearn.linear_model import LogisticRegression
from sklearn.ensemble import RandomForestClassifier, VotingClassifier
clf1 = LogisticRegression(random_state=1)
clf2 = RandomForestClassifier(random_state=1)
clf3 = XGBClassifier(learning_rate=0.1, n_estimators=150, max_depth=4, min_child_weight=2, subsample=0.7,objective=\'binary:logistic\')
 
vclf = VotingClassifier(estimators=[(\'lr\', clf1), (\'rf\', clf2), (\'xgb\', clf3)], voting=\'soft\', weights=[2, 1, 1])
vclf = vclf .fit(x_train,y_train)
print(vclf .predict(x_test))

5.1.3 Stacking：

import warnings
warnings.filterwarnings(\'ignore\')
import itertools
import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt
import matplotlib.gridspec as gridspec
from sklearn import datasets
from sklearn.linear_model import LogisticRegression
from sklearn.neighbors import KNeighborsClassifier
from sklearn.naive_bayes import GaussianNB 
from sklearn.ensemble import RandomForestClassifier
from mlxtend.classifier import StackingClassifier
from sklearn.model_selection import cross_val_score, train_test_split
from mlxtend.plotting import plot_learning_curves
from mlxtend.plotting import plot_decision_regions


# 以python自带的鸢尾花数据集为例
iris = datasets.load_iris()
X, y = iris.data[:, 1:3], iris.target


clf1 = KNeighborsClassifier(n_neighbors=1)
clf2 = RandomForestClassifier(random_state=1)
clf3 = GaussianNB()
lr = LogisticRegression()
sclf = StackingClassifier(classifiers=[clf1, clf2, clf3], 
                          meta_classifier=lr)


label = [\'KNN\', \'Random Forest\', \'Naive Bayes\', \'Stacking Classifier\']
clf_list = [clf1, clf2, clf3, sclf]
    
fig = plt.figure(figsize=(10,8))
gs = gridspec.GridSpec(2, 2)
grid = itertools.product([0,1],repeat=2)


clf_cv_mean = []
clf_cv_std = []
for clf, label, grd in zip(clf_list, label, grid):
        
    scores = cross_val_score(clf, X, y, cv=5, scoring=\'accuracy\')
    print("Accuracy: %.2f (+/- %.2f) [%s]" %(scores.mean(), scores.std(), label))
    clf_cv_mean.append(scores.mean())
    clf_cv_std.append(scores.std())
        
    clf.fit(X, y)
    ax = plt.subplot(gs[grd[0], grd[1]])
    fig = plot_decision_regions(X=X, y=y, clf=clf)
    plt.title(label)
 

plt.show()

Accuracy: 0.91 (+/- 0.07) [KNN]
Accuracy: 0.94 (+/- 0.04) [Random Forest]
Accuracy: 0.91 (+/- 0.04) [Naive Bayes]
Accuracy: 0.94 (+/- 0.04) [Stacking Classifier]

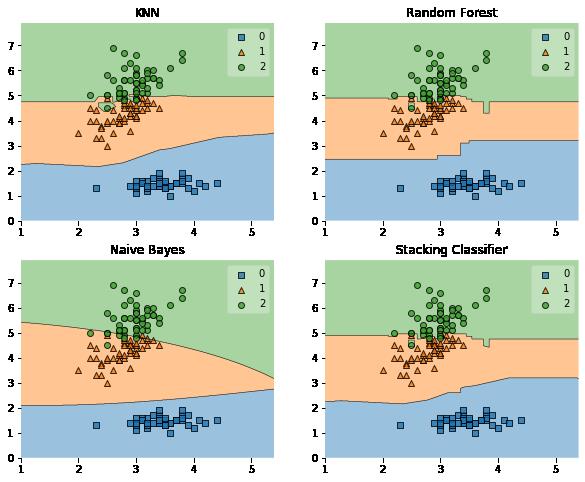
5.1.2 blending

# 以python自带的鸢尾花数据集为例
data_0 = iris.data
data = data_0[:100,:]


target_0 = iris.target
target = target_0[:100]
 
#模型融合中基学习器
clfs = [LogisticRegression(),
        RandomForestClassifier(),
        ExtraTreesClassifier(),
        GradientBoostingClassifier()]
 
#切分一部分数据作为测试集
X, X_predict, y, y_predict = train_test_split(data, target, test_size=0.3, random_state=914)


#切分训练数据集为d1,d2两部分
X_d1, X_d2, y_d1, y_d2 = train_test_split(X, y, test_size=0.5, random_state=914)
dataset_d1 = np.zeros((X_d2.shape[0], len(clfs)))
dataset_d2 = np.zeros((X_predict.shape[0], len(clfs)))
 
for j, clf in enumerate(clfs):
    #依次训练各个单模型
    clf.fit(X_d1, y_d1)
    y_submission = clf.predict_proba(X_d2)[:, 1]
    dataset_d1[:, j] = y_submission
    #对于测试集，直接用这k个模型的预测值作为新的特征。
    dataset_d2[:, j] = clf.predict_proba(X_predict)[:, 1]
    print("val auc Score: %f" % roc_auc_score(y_predict, dataset_d2[:, j]))


#融合使用的模型
clf = GradientBoostingClassifier()
clf.fit(dataset_d1, y_d2)
y_submission = clf.predict_proba(dataset_d2)[:, 1]
print("Val auc Score of Blending: %f" % (roc_auc_score(y_predict, y_submission)))

5.2 小结总结

简单平均和加权平均是常用的两种比赛中模型融合的方式。其优点是快速、简单。
stacking在众多比赛中大杀四方，但是跑过代码的小伙伴想必能感受到速度之慢，同时stacking多层提升幅度并不能抵消其带来的时间和内存消耗，所以实际环境中应用还是有一定的难度，同时在有答辩环节的比赛中，主办方也会一定程度上考虑模型的复杂程度，所以说并不是模型融合的层数越多越好的。
当然在比赛中将加权平均、stacking、blending等混用也是一种策略，可能会收获意想不到的效果哦！

6.完整baseline代码

import pandas as pd
import os
import gc
import lightgbm as lgb
import xgboost as xgb
from catboost import CatBoostRegressor
from sklearn.linear_model import SGDRegressor, LinearRegression, Ridge
from sklearn.preprocessing import MinMaxScaler
import math
import numpy as np
from tqdm import tqdm
from sklearn.model_selection import StratifiedKFold, KFold
from sklearn.metrics import accuracy_score, f1_score, roc_auc_score, log_loss
import matplotlib.pyplot as plt
import time
import warnings
warnings.filterwarnings(\'ignore\')

train = pd.read_csv(\'train.csv\')
testA = pd.read_csv(\'testA.csv\')

train.head()

data = pd.concat([train, testA], axis=0, ignore_index=True)

6.1数据预处理

可以看到很多变量不能直接训练，比如grade、subGrade、employmentLength、issueDate、earliesCreditLine，需要进行预处理

print(sorted(data[\'grade\'].unique()))
print(sorted(data[\'subGrade\'].unique()))

[\'A\', \'B\', \'C\', \'D\', \'E\', \'F\', \'G\']
[\'A1\', \'A2\', \'A3\', \'A4\', \'A5\', \'B1\', \'B2\', \'B3\', \'B4\', \'B5\', \'C1\', \'C2\', \'C3\', \'C4\', \'C5\', \'D1\', \'D2\', \'D3\', \'D4\', \'D5\', \'E1\', \'E2\', \'E3\', \'E4\', \'E5\', \'F1\', \'F2\', \'F3\', \'F4\', \'F5\', \'G1\', \'G2\', \'G3\', \'G4\', \'G5\']

data[\'employmentLength\'].value_counts(dropna=False).sort_index()

1 year        65671
10+ years    328525
2 years       90565
3 years       80163
4 years       59818
5 years       62645
6 years       46582
7 years       44230
8 years       45168
9 years       37866
< 1 year      80226
NaN           58541
Name: employmentLength, dtype: int64

首先对employmentLength进行转换到数值

data[\'employmentLength\'].replace(to_replace=\'10+ years\', value=\'10 years\', inplace=True)
data[\'employmentLength\'].replace(\'< 1 year\', \'0 years\', inplace=True)

def employmentLength_to_int(s):
    if pd.isnull(s):
        return s
    else:
        return np.int8(s.split()[0])
    
data[\'employmentLength\'] = data[\'employmentLength\'].apply(employmentLength_to_int)

data[\'employmentLength\'].value_counts(dropna=False).sort_index()

0.0      80226
1.0      65671
2.0      90565
3.0      80163
4.0      59818
5.0      62645
6.0      46582
7.0      44230
8.0      45168
9.0      37866
10.0    328525
NaN      58541
Name: employmentLength, dtype: int64

对earliesCreditLine进行预处理

data[\'earliesCreditLine\'].sample(5)

375743    Jun-2003
361340    Jul-1999
716602    Aug-1995
893559    Oct-1982
221525    Nov-2004
Name: earliesCreditLine, dtype: object

data[\'earliesCreditLine\'] = data[\'earliesCreditLine\'].apply(lambda s: int(s[-4:]))

data[\'earliesCreditLine\'].describe()

count    1000000.000000
mean        1998.688632
std            7.606231
min         1944.000000
25%         1995.000000
50%         2000.000000
75%         2004.000000
max         2015.000000
Name: earliesCreditLine, dtype: float64

data.head()

类别特征处理

# 部分类别特征
cate_features = [\'grade\', \'subGrade\', \'employmentTitle\', \'homeOwnership\', \'verificationStatus\', \'purpose\', \'postCode\', \'regionCode\', \\
                 \'applicationType\', \'initialListStatus\', \'title\', \'policyCode\']
for f in cate_features:
    print(f, \'类型数：\', data[f].nunique())

grade 类型数： 7
subGrade 类型数： 35
employmentTitle 类型数： 298101
homeOwnership 类型数： 6
verificationStatus 类型数： 3
purpose 类型数： 14
postCode 类型数： 935
regionCode 类型数： 51
applicationType 类型数： 2
initialListStatus 类型数： 2
title 类型数： 47903
policyCode 类型数： 1

# 类型数在2之上，又不是高维稀疏的
data = pd.get_dummies(data, columns=[\'grade\', \'subGrade\', \'homeOwnership\', \'verificationStatus\', \'purpose\', \'regionCode\'], drop_first=True)

# 高维类别特征需要进行转换
for f in [\'employmentTitle\', \'postCode\', \'title\']:
    data[f+\'_cnts\'] = data.groupby([f])[\'id\'].transform(\'count\')
    data[f+\'_rank\'] = data.groupby([f])[\'id\'].rank(ascending=False).astype(int)
    del data[f]

6.2训练数据/测试数据准备

features = [f for f in data.columns if f not in [\'id\',\'issueDate\',\'isDefault\']]

train = data[data.isDefault.notnull()].reset_index(drop=True)
test = data[data.isDefault.isnull()].reset_index(drop=True)

x_train = train[features]
x_test = test[features]

y_train = train[\'isDefault\']

6.3模型训练

直接构建了一个函数，可以调用三种树模型，方便快捷

def cv_model(clf, train_x, train_y, test_x, clf_name):
    folds = 5
    seed = 2020
    kf = KFold(n_splits=folds, shuffle=True, random_state=seed)

    train = np.zeros(train_x.shape[0])
    test = np.zeros(test_x.shape[0])

    cv_scores = []

    for i, (train_index, valid_index) in enumerate(kf.split(train_x, train_y)):
        print(\'************************************  ************************************\'.format(str(i+1)))
        trn_x, trn_y, val_x, val_y = train_x.iloc[train_index], train_y[train_index], train_x.iloc[valid_index], train_y[valid_index]

        if clf_name == "lgb":
            train_matrix = clf.Dataset(trn_x, label=trn_y)
            valid_matrix = clf.Dataset(val_x, label=val_y)

            params = 
                \'boosting_type\': \'gbdt\',
                \'objective\': \'binary\',
                \'metric\': \'auc\',
                \'min_child_weight\': 5,
                \'num_leaves\': 2 ** 5,
                \'lambda_l2\': 10,
                \'feature_fraction\': 0.8,
                \'bagging_fraction\': 0.8,
                \'bagging_freq\': 4,
                \'learning_rate\': 0.1,
                \'seed\': 2020,
                \'nthread\': 28,
                \'n_jobs\':24,
                \'silent\': True,
                \'verbose\': -1,
            

            model = clf.train(params, train_matrix, 50000, valid_sets=[train_matrix, valid_matrix], verbose_eval=200,early_stopping_rounds=200)
            val_pred = model.predict(val_x, num_iteration=model.best_iteration)
            test_pred = model.predict(test_x, num_iteration=model.best_iteration)
            
            # print(list(sorted(zip(features, model.feature_importance("gain")), key=lambda x: x[1], reverse=True))[:20])
                
        if clf_name == "xgb":
            train_matrix = clf.DMatrix(trn_x , label=trn_y)
            valid_matrix = clf.DMatrix(val_x , label=val_y)
            test_matrix = clf.DMatrix(test_x)
            
            params = \'booster\': \'gbtree\',
                      \'objective\': \'binary:logistic\',
                      \'eval_metric\': \'auc\',
                      \'gamma\': 1,
                      \'min_child_weight\': 1.5,
                      \'max_depth\': 5,
                      \'lambda\': 10,
                      \'subsample\': 0.7,
                      \'colsample_bytree\': 0.7,
                      \'colsample_bylevel\': 0.7,
                      \'eta\': 0.04,
                      \'tree_method\': \'exact\',
                      \'seed\': 2020,
                      \'nthread\': 36,
                      "silent": True,
                      
            
            watchlist = [(train_matrix, \'train\'),(valid_matrix, \'eval\')]
            
            model = clf.train(params, train_matrix, num_boost_round=50000, evals=watchlist, verbose_eval=200, early_stopping_rounds=200)
            val_pred  = model.predict(valid_matrix, ntree_limit=model.best_ntree_limit)
            test_pred = model.predict(test_matrix , ntree_limit=model.best_ntree_limit)
                 
        if clf_name == "cat":
            params = \'learning_rate\': 0.05, \'depth\': 5, \'l2_leaf_reg\': 10, \'bootstrap_type\': \'Bernoulli\',
                      \'od_type\': \'Iter\', \'od_wait\': 50, \'random_seed\': 11, \'allow_writing_files\': False
            
            model = clf(iterations=20000, **params)
            model.fit(trn_x, trn_y, eval_set=(val_x, val_y),
                      cat_features=[], use_best_model=True, verbose=500)
            
            val_pred  = model.predict(val_x)
            test_pred = model.predict(test_x)
            
        train[valid_index] = val_pred
        test = test_pred / kf.n_splits
        cv_scores.append(roc_auc_score(val_y, val_pred))
        
        print(cv_scores)
       
    print("%s_scotrainre_list:" % clf_name, cv_scores)
    print("%s_score_mean:" % clf_name, np.mean(cv_scores))
    print("%s_score_std:" % clf_name, np.std(cv_scores))
    return train, test

def lgb_model(x_train, y_train, x_test):
    lgb_train, lgb_test = cv_model(lgb, x_train, y_train, x_test, "lgb")
    return lgb_train, lgb_test

def xgb_model(x_train, y_train, x_test):
    xgb_train, xgb_test = cv_model(xgb, x_train, y_train, x_test, "xgb")
    return xgb_train, xgb_test

def cat_model(x_train, y_train, x_test):
    cat_train, cat_test = cv_model(CatBoostRegressor, x_train, y_train, x_test, "cat") 
    return cat_train, cat_test

lgb_train, lgb_test = lgb_model(x_train, y_train, x_test)

[706]	training\'s auc: 0.771324	valid_1\'s auc: 0.731887
[0.7320814878889421, 0.7279015876934286, 0.7331203287449972, 0.731886588682118]
************************************ 5 ************************************
Training until validation scores don\'t improve for 200 rounds.
[200]	training\'s auc: 0.743113	valid_1\'s auc: 0.729226
[400]	training\'s auc: 0.7559	valid_1\'s auc: 0.730816
[600]	training\'s auc: 0.766388	valid_1\'s auc: 0.73092
[800]	training\'s auc: 0.77627	valid_1\'s auc: 0.731029
[1000]	training\'s auc: 0.785791	valid_1\'s auc: 0.730933
Early stopping, best iteration is:
[883]	training\'s auc: 0.780369	valid_1\'s auc: 0.731096
[0.7320814878889421, 0.7279015876934286, 0.7331203287449972, 0.731886588682118, 0.7310960057774112]
lgb_scotrainre_list: [0.7320814878889421, 0.7279015876934286, 0.7331203287449972, 0.731886588682118, 0.7310960057774112]
lgb_score_mean: 0.7312171997573793
lgb_score_std: 0.001779041696522632

xgb_train, xgb_test = xgb_model(x_train, y_train, x_test)

Will train until eval-auc hasn\'t improved in 200 rounds.
[200]	train-auc:0.728072	eval-auc:0.722913
[400]	train-auc:0.735517	eval-auc:0.726582
[600]	train-auc:0.740782	eval-auc:0.728449
[800]	train-auc:0.745258	eval-auc:0.729653
[1000]	train-auc:0.749185	eval-auc:0.730489
[1200]	train-auc:0.752723	eval-auc:0.731038
[1400]	train-auc:0.755985	eval-auc:0.731466
[1600]	train-auc:0.759166	eval-auc:0.731758
[1800]	train-auc:0.762205	eval-auc:0.73199
[2000]	train-auc:0.765197	eval-auc:0.732145
[2200]	train-auc:0.767976	eval-auc:0.732194
Stopping. Best iteration:
[2191]	train-auc:0.767852	eval-auc:0.732213

[0.7332460852050292, 0.7300358478747684, 0.7344942212088965, 0.7334876284761012, 0.7322134048106561]
xgb_scotrainre_list: [0.7332460852050292, 0.7300358478747684, 0.7344942212088965, 0.7334876284761012, 0.7322134048106561]
xgb_score_mean: 0.7326954375150903
xgb_score_std: 0.0015147392354657807

cat_train, cat_test = cat_model(x_train, y_train, x_test)

Shrink model to first 3433 iterations.
[0.7326058985428212, 0.7292909146788396, 0.7341207611812285, 0.7324483603137153]
************************************ 5 ************************************
0:	learn: 0.4409876	test: 0.4409159	best: 0.4409159 (0)	total: 52.3ms	remaining: 17m 26s
500:	learn: 0.3768055	test: 0.3776229	best: 0.3776229 (500)	total: 38s	remaining: 24m 38s
1000:	learn: 0.3752600	test: 0.3768397	best: 0.3768397 (1000)	total: 1m 15s	remaining: 23m 57s
1500:	learn: 0.3741843	test: 0.3764855	best: 0.3764855 (1500)	total: 1m 53s	remaining: 23m 16s
2000:	learn: 0.3732691	test: 0.3762491	best: 0.3762490
零基础入门金融风控-贷款违约预测-机器学习-数据分析


        
                
                    
                    零基础入门金融风控-贷款违约预测 
一、赛题数据 
赛题以预测用户贷款是否违约为任务，数据集报名后可见并可下载，该数据来自某信贷平台的贷款记录，总数据量超过120w，包含47列变量信息，其中15列为匿名变量。为了保证比赛的公平性，将会从中抽取80万条作为训练集，20万条作为测试集A，20万条作为测试集B，同时会对employmentTitle、purpose、postCode和title等信息进行脱敏。 
数据可在阿里云学习赛中获得。 
字段表 
id Field Description
1 id 为贷款清单分配的唯一信用证标识
2 loanAmnt 贷款金额
3 term 贷款期限（year）
4 interestRate 贷款利率
5 installment 分期付款金额
6 grade 贷款等级
7 subGrade 贷款等级之子级
8 employmentTitle 就业职称
9 employmentLength 就业年限（年）
10 homeOwnership 借款人在登记时提供的房屋所有权状况
11 annualIncome 年收入
12 verificationStatus 验证状态
13 issueDate 贷款发放的月份
14 purpose 借款人在贷款申请时的贷款用途类别
15 postCode 借款人在贷款申请中提供的邮政编码的前3位数字
16 regionCode 地区编码
17 dti 债务收入比
18 delinquency_2years 借款人过去2年信用档案中逾期30天以上的违约事件数
19 ficoRangeLow 借款人在贷款发放时的fico所属的下限范围
20 ficoRangeHigh 借款人在贷款发放时的fico所属的上限范围
21 openAcc 借款人信用档案中未结信用额度的数量
22 pubRec 贬损公共记录的数量
23 pubRecBankruptcies 公开记录清除的数量
24 revolBal 信贷周转余额合计
25 revolUtil 循环额度利用率，或借款人使用的相对于所有可用循环信贷的信贷金额
26 totalAcc 借款人信用档案中当前的信用额度总数
27 initialListStatus 贷款的初始列表状态
28 applicationType 表明贷款是个人申请还是与两个共同借款人的联合申请
29 earliesCreditLine 借款人最早报告的信用额度开立的月份
30 title 借款人提供的贷款名称
31 policyCode 公开可用的策略_代码=1新产品不公开可用的策略_代码=2
32 n系列匿名特征 匿名特征n0-n14，为一些贷款人行为计数特征的处理
二、评测标准 
提交结果为每个测试样本是1的概率，也就是y为1的概率。评价方法为AUC评估模型效果（越大越好）。 
三、代码演示 
说明：下面运行结果贴出的是部分图。
环境：本案例使用的库 
  pandas 1.3.2
matplotlib 3.4.3
seaborn 0.11.2
numpy 1.21.2
scipy 1.4.1
scikit-learn 0.24.2
 
使用的是jupyter notebook 
1. 数据分析及处理 
1.1.0导入相关库 
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
import numpy as np
from scipy import stats
import matplotlib as mpl
#显示所有列
pd.set_option('display.max_columns',None)
# 警告处理 
import warnings
warnings.filterwarnings('ignore')
%matplotlib inline
 
1.1.1数据预处理 
df_train = pd.read_csv('train.csv')
df_test = pd.read_csv('testA.csv')
 
df_train.shape, df_test.shape
 
 
df_train['train_test'] = 'train'
df_test['train_test'] = 'test'
 
合并训练集和测试集 
df = df_train.append(df_test)
df.reset_index(inplace=True)
df.drop('index',inplace=True,axis=1)
display(df.head())
 
 
df.info()
 

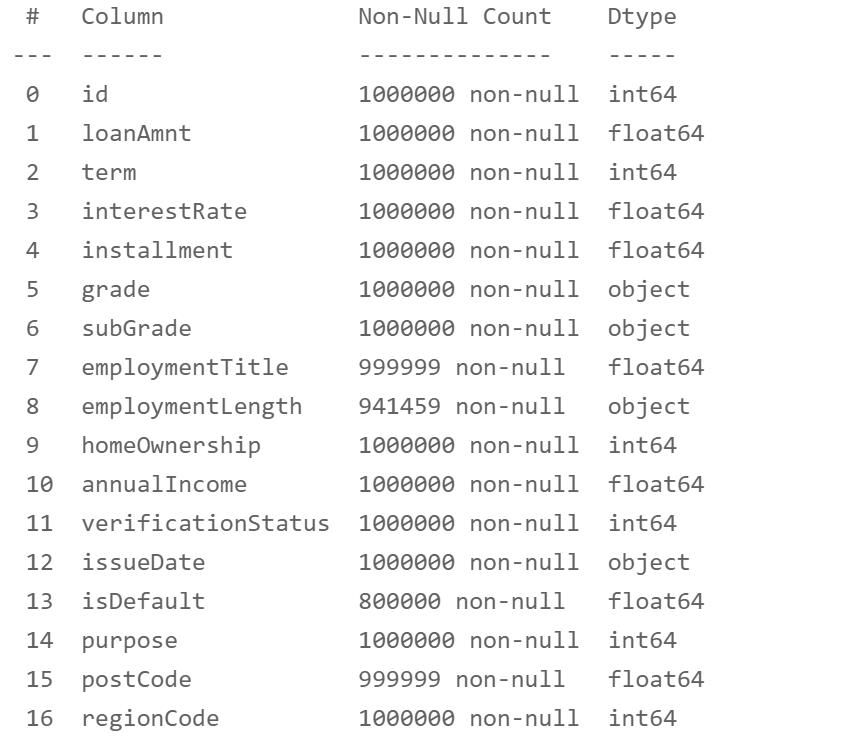
 缺失值处理 
# 需要处理的列名
is_na_cols = [
    'employmentTitle', 'employmentLength', 'postCode', 'dti', 'pubRecBankruptcies',
    'revolUtil', 'title',] + [f'n{i}' for i in range(15)]
 
对缺失值 用众数填充 
# 对缺失值 用众数填充
for i in range(len(is_na_cols)):
    most_num = df[is_na_cols[i]].value_counts().index[0]
    df[is_na_cols[i]] = df[is_na_cols[i]].fillna(most_num)
df.info()
 

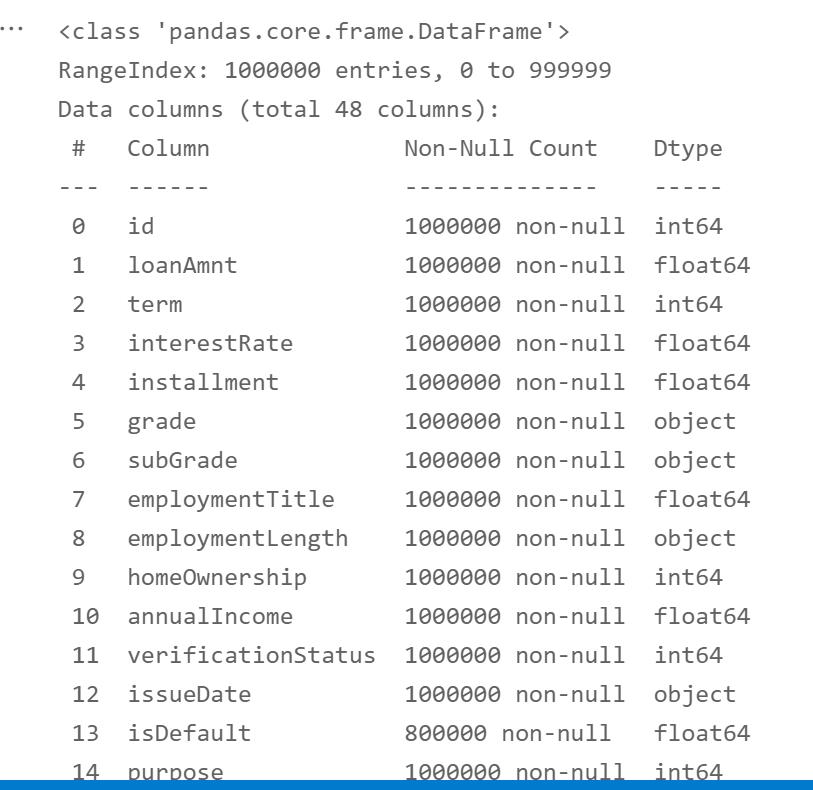
 分开训练集和测试集 
df_train = df[df['train_test'] == 'train']
df_test = df[df['train_test'] == 'test']
 

del df_train['train_test']
del df_test['train_test']
 
df_train.shape, df_test.shape
 

 删除测试集的预测目标 
del df_test['isDefault']
 
1.1.2数值型变量和非数值型变量的处理与分析 
# 非数值型
non_numeric_cols = [
    'grade', 'subGrade', 'employmentLength', 'issueDate', 'earliesCreditLine'
]
# 数值型
numeric_cols = [
    x for x in df_test.columns if x not in non_numeric_cols + ['isDefault']
]
non_numeric_cols, numeric_cols
 
 
1.1.3数值型(numeric_cols)测试集与训练集分布 
画箱式图可查看哪些列名是连续型和非连续型变量 
# 画箱式图
column = numeric_cols # 列表头
fig = plt.figure(figsize=(20, 40))  # 指定绘图对象宽度和高度
for i in range(len(column)):
    plt.subplot(13, 4, i + 1)  # 13行3列子图
    sns.boxplot(df[column[i]], orient="v", width=0.5)  # 箱式图
    plt.ylabel(column[i], fontsize=8)
plt.show()
 
 
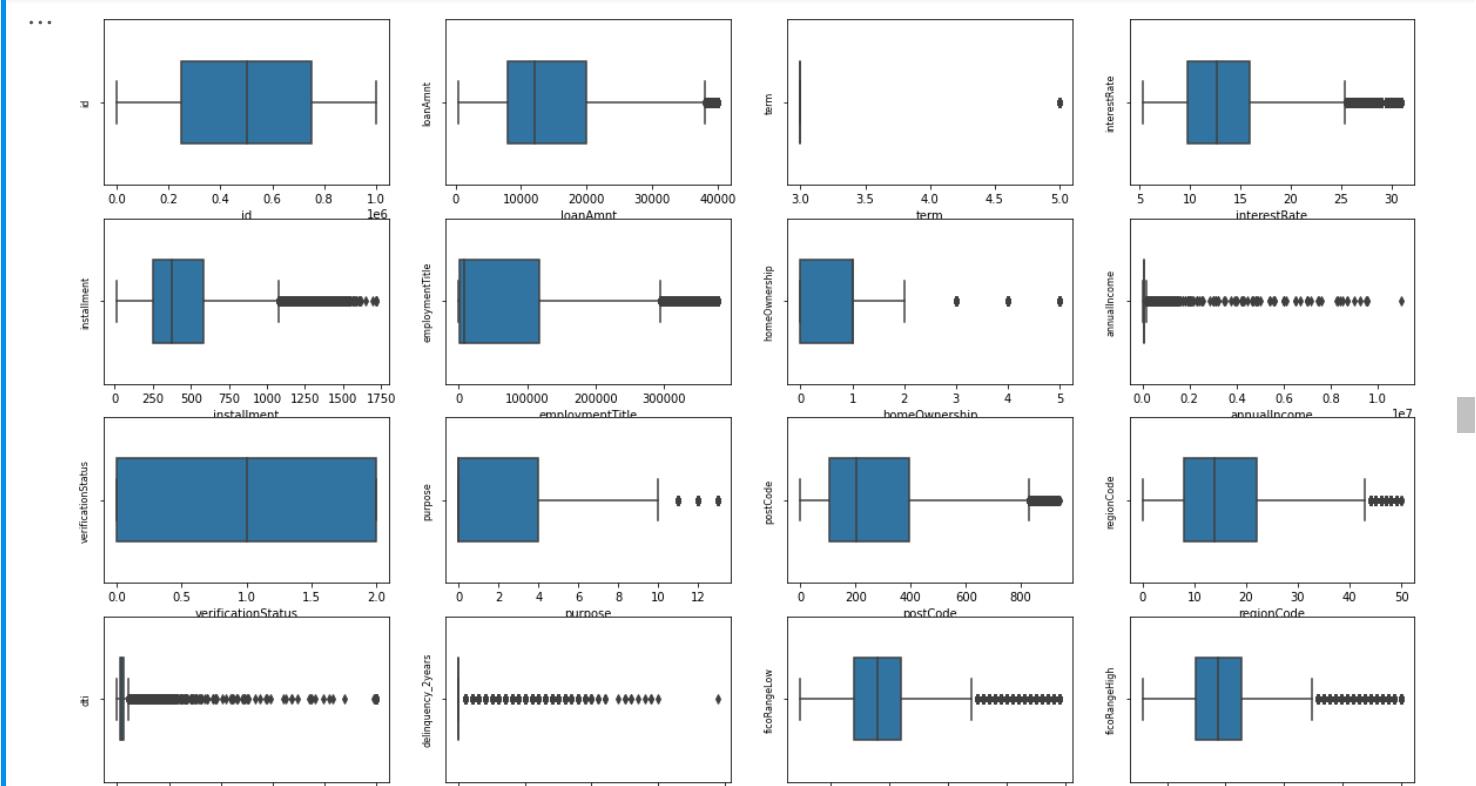
1.1.4取出数值连续性变量，查看数据分布 
continuous_cols = [
    'id', 'loanAmnt', 'interestRate', 'installment', 'employmentTitle', 'homeOwnership',
    'annualIncome', 'purpose', 'postCode', 'regionCode', 'dti', 'delinquency_2years',
    'ficoRangeLow', 'ficoRangeHigh', 'openAcc', 'pubRec', 'revolBal', 'revolUtil','totalAcc',
    'title', 'n14'
] + [f'n{i}' for i in range(11)] 
non_continuous_cols = [
    x for x in numeric_cols if x not in continuous_cols
]
 
可视化正太分布，查看测试集与训练集的数据是否相同，相同可保留，差距会影响预测结果，就去除。 
dist_cols = 6
dist_rows = len(df_test[continuous_cols].columns)
plt.figure(figsize=(4*dist_cols,4*dist_rows))

i=1
for col in df_test[continuous_cols].columns:
    ax=plt.subplot(dist_rows,dist_cols,i)
    ax = sns.kdeplot(df_train[continuous_cols][col], color="Red", shade=True)
    ax = sns.kdeplot(df_test[continuous_cols][col], color="Blue", shade=True)
    ax.set_xlabel(col)
    ax.set_ylabel("Frequency")
    ax = ax.legend(["train","test"])
    
    i+=1
plt.show()
 
 
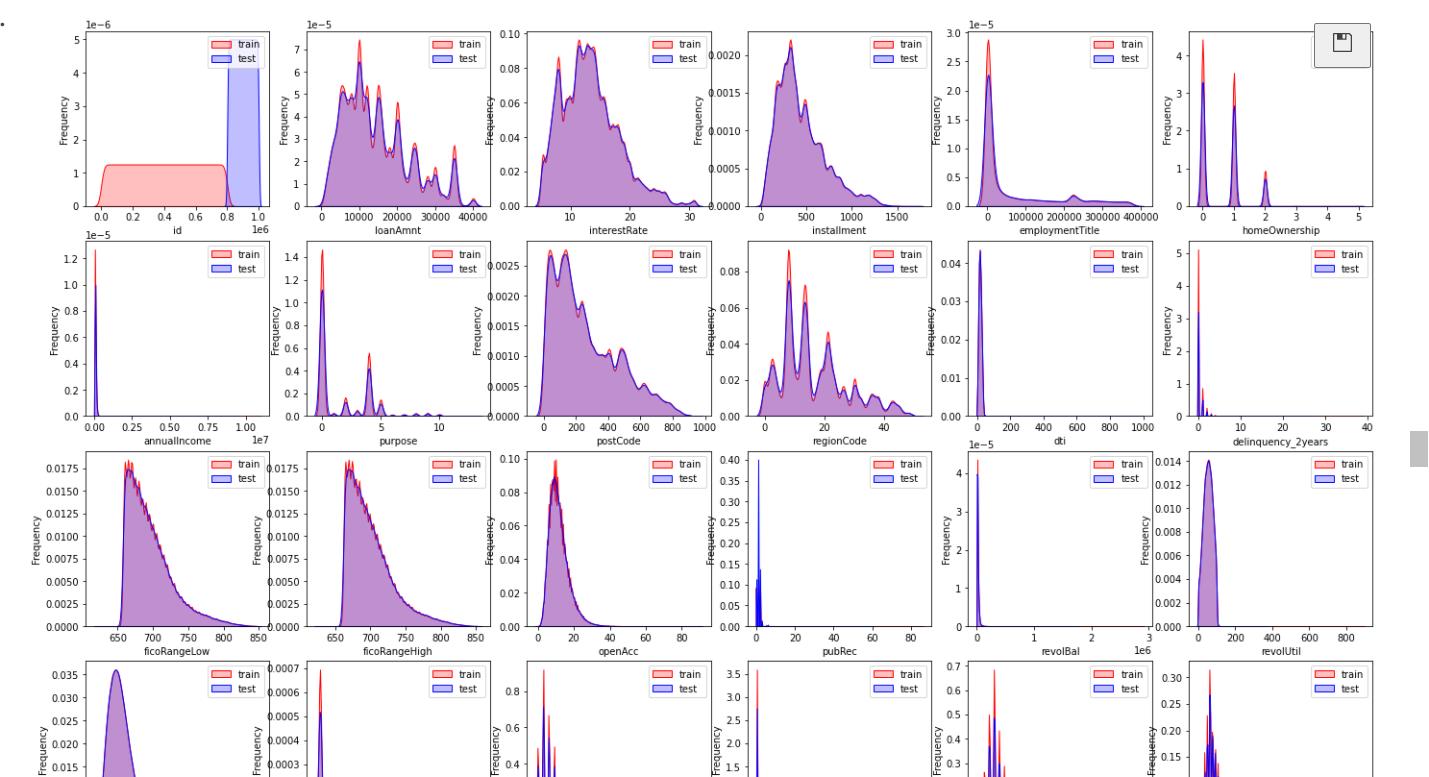
画QQ图及正态分布图 
QQ图：曲线越接近直线，越接近正态分布，预测效果更好。 
train_cols = 6
train_rows = len(df[continuous_cols].columns)
plt.figure(figsize=(4*train_cols,4*train_rows))

i=0
for col in df[continuous_cols].columns:
    i+=1
    ax=plt.subplot(train_rows,train_cols,i)
    sns.distplot(df[continuous_cols][col],fit=stats.norm)
    i+=1
    ax=plt.subplot(train_rows,train_cols,i)
    res = stats.probplot(df[continuous_cols][col], plot=plt)
plt.show()
 

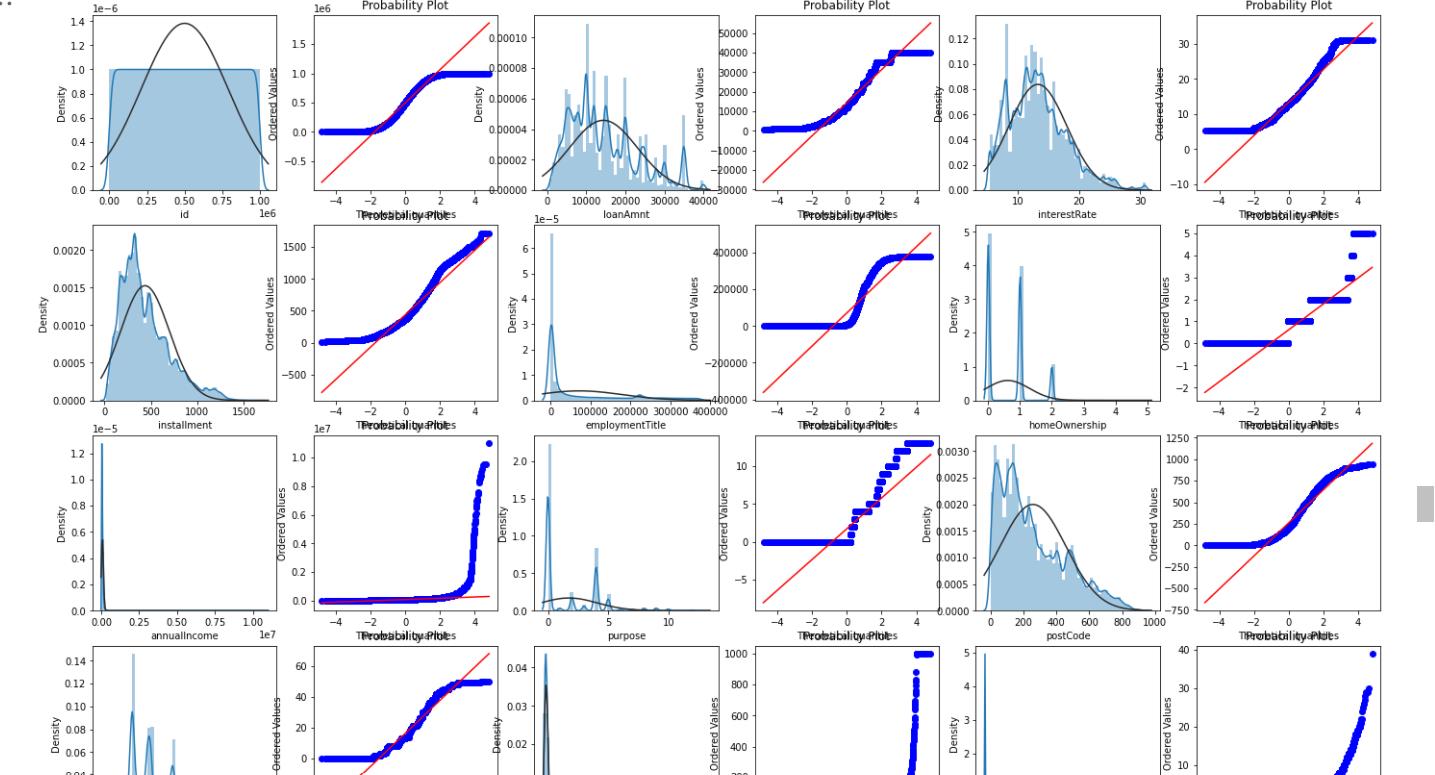
 训练集的数据和测试集的数据分布差不多可以将他们整合到一起进行处理 
1.1.5查看数值非连续性型数据分布 
for i in range(len(non_continuous_cols)):
    print("%s这列的非连续性数据的分布："%non_continuous_cols[i])
    print(df[non_continuous_cols[i]].value_counts())
 
 
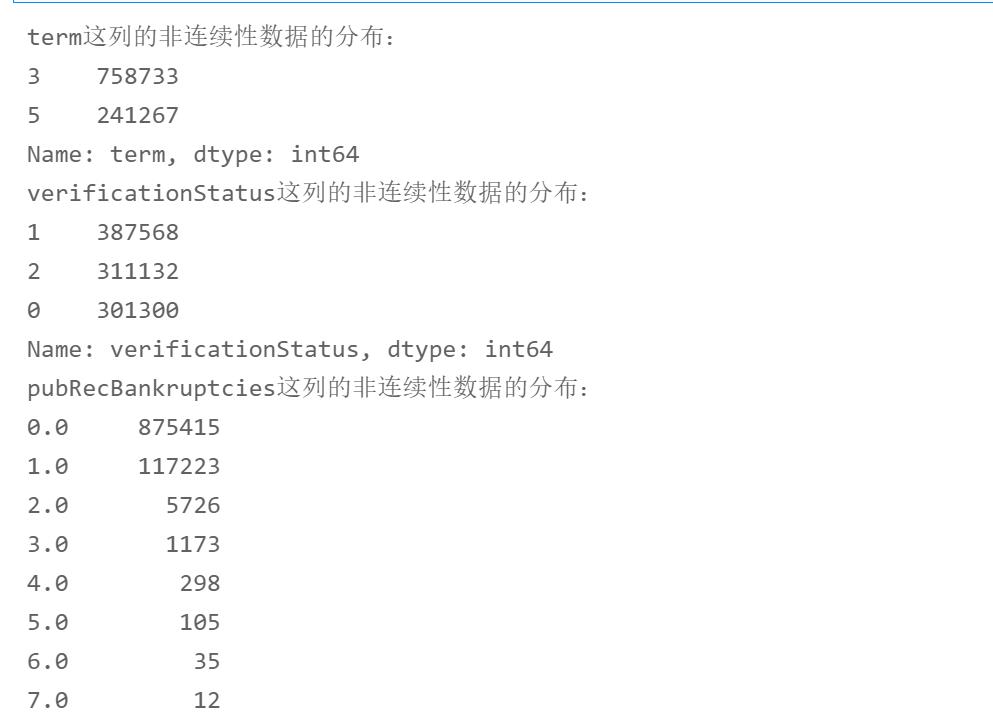
1.1.6查看非数值型数据分布 
for i in range(len(non_numeric_cols)):
    print("%s这列非数值型数据的分布：\\n"%non_numeric_cols[i])
    print(df[non_numeric_cols[i]].value_counts())
 
 
2. 特征工程 
2.1.1 数值非连续性型数据处理 
policyCode字段 
df['policyCode'].describe()
 
 
# 字段只有一个值，不用了
df.drop('policyCode',axis=1,inplace=True)
 
n13字段 
df['n13'] = df['n13'].apply(lambda x: 1 if x not in [0] else x)
df['n13'].value_counts()
 
 
2.1.2 非数值型数据 
grade字段 
# 非数值型编码
from sklearn.preprocessing import LabelEncoder
le = LabelEncoder()
df['grade'] = le.fit_transform(df['grade'])
df['grade'].value_counts()
 

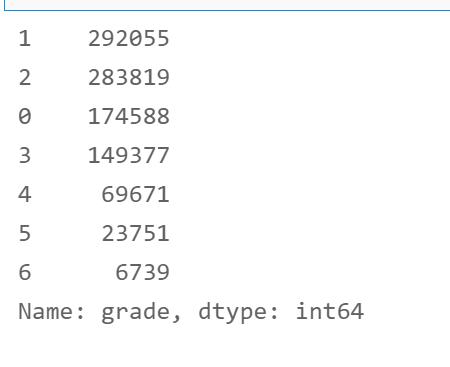
 2. subGrade字段 
from sklearn.preprocessing import LabelEncoder
le = LabelEncoder()
df['subGrade'] = le.fit_transform(df['subGrade'])
df['subGrade'].value_counts()
 

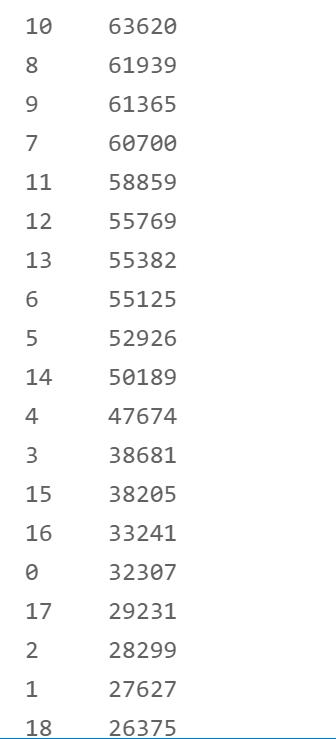
 3. employmentLength字段 
# 构造编码函数
def encoder(x):
    if x[:-5] == '10+ ':
        return 10
    elif x[:-5] == '< 1':
        return 0
    else:
        return int(x[0])
df['employmentLength'] = df['employmentLength'].apply(encoder)
df['employmentLength'].value_counts()
 

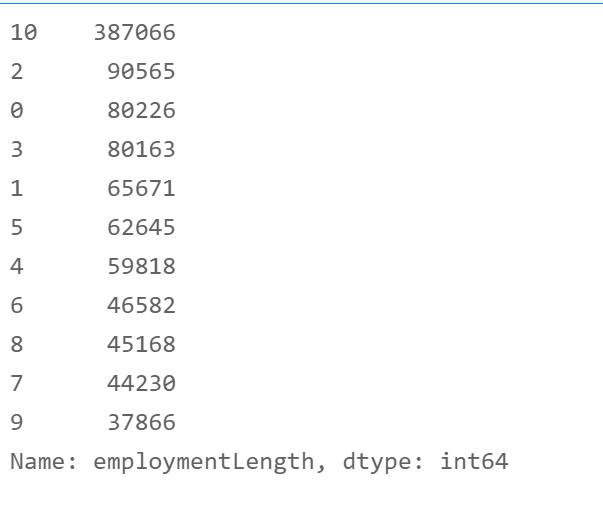
 4. issueDate字段 
计算离现在多少月就ok了 
from datetime import datetime
def encoder1(x):
    x = str(x)
    now = datetime.strptime('2020-07-01','%Y-%m-%d')
    past = datetime.strptime(x,'%Y-%m-%d')
    period = now - past
    period = period.days
    return round(period / 30, 2)
df['issueDate'] = df['issueDate'].apply(encoder1)
df['issueDate'].value_counts()
 

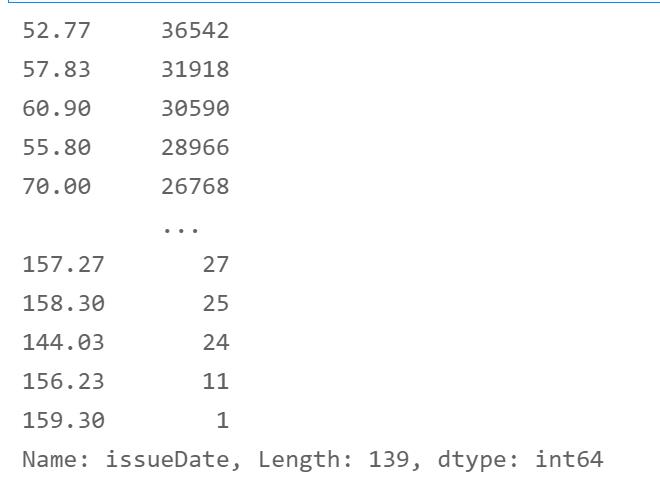
 5. earliesCreditLine字段 
def encoder2(x):
    if x[:3] == 'Jan':
        return x[-4:] + '-' + '01-01'
    if x[:3] == 'Feb':
        return x[-4:] + '-' + '02-01'
    if x[:3] == 'Mar':
        return x[-4:] + '-' + '03-01'
    if x[:3] == 'Apr':
        return x[-4:] + '-' + '04-01'
    if x[:3] == 'May':
        return x[-4:] + '-' + '05-01'
    if x[:3] == 'Jun':
        return x[-4:] + '-' + '06-01'
    if x[:3] == 'Jul':
        return x[-4:] + '-' + '07-01'
    if x[:3] == 'Aug':
        return x[-4:] + '-' + '08-01'
    if x[:3] == 'Sep':
        return x[-4:] + '-' + '09-01'
    if x[:3] == 'Oct':
        return x[-4:] + '-' + '10-01'
    if x[:3] == 'Nov':
        return x[-4:] + '-' + '11-01'
    if x[:3] == 'Dec':
        return x[-4:] + '-' + '12-01'
df['earliesCreditLine'] = df['earliesCreditLine'].apply(encoder2)
df['earliesCreditLine'].value_counts()
 
 
df['earliesCreditLine'] = df['earliesCreditLine'].apply(encoder1)
df['earliesCreditLine'].value_counts()
 
 
3. 保存文件 
train = df[df['train_test'] == 'train']
test = df[df['train_test'] == 'test']
 
del test['isDefault']
 
del train['train_test']
del test['train_test']
 
train.to_csv('train_process.csv')
test.to_csv('test_process.csv')
 
4. 数据建模 
4.1.1数据查看 
# 数据处理
import numpy as np
import pandas as pd

# 数据可视化
import matplotlib.pyplot as plt

# 特征选择和编码
from sklearn.preprocessing import LabelEncoder

# 机器学习
from sklearn import model_selection, tree, preprocessing, metrics
from sklearn.ensemble import RandomForestClassifier, GradientBoostingClassifier
from sklearn.linear_model import LinearRegression, LogisticRegression, Ridge, Lasso, SGDClassifier
from sklearn.tree import DecisionTreeClassifier

# 网格搜索、随机搜索
import scipy.stats as st
from sklearn.model_selection import GridSearchCV
from sklearn.model_selection import RandomizedSearchCV

# 模型度量（分类）
from sklearn.metrics import precision_recall_fscore_support, roc_curve, auc

# 警告处理 
import warnings
warnings.filterwarnings('ignore')

# 在Jupyter上画图
%matplotlib inline
 
train = pd.read_csv('train_process.csv')
test = pd.read_csv('test_process.csv')
train.shape, test.shape
 
 
train.columns,test.columns
 
 
# 删除Unnamed: 0
del train['Unnamed: 0']
del test['Unnamed: 0']
 
## 为了正确评估模型性能，将数据划分为训练集和测试集，并在训练集上训练模型，在测试集上验证模型性能。
from sklearn.model_selection import train_test_split

## 选择其类别为0和1的样本 （不包括类别为2的样本）
data_target_part = train['isDefault']
data_features_part = train[[x for x in train.columns if x != 'isDefault' and 'id']]

## 测试集大小为20%， 80%/20%分
x_train, x_test, y_train, y_test = train_test_split(data_features_part, data_target_part, test_size = 0.2, random_state = 2020)
 
x_train.head()
 
 
y_train.head()
 
 
4.1.1选择算法 
以下是用到的算法. 
Logistic Regression
Random Forest
Decision Tree
Gradient Boosted Trees 
# 绘制AUC曲线
import time
def plot_roc_curve以上是关于数据挖掘实践（金融风控）：金融风控之贷款违约预测挑战赛（下篇）[xgboots/lightgbm/Catboost等模型]--模型融合：stackingblending的主要内容，如果未能解决你的问题，请参考以下文章 
 零基础入门金融风控-贷款违约预测-机器学习-数据分析
 基于机器学习与深度学习的金融风控贷款违约预测
 基于机器学习与深度学习的金融风控贷款违约预测
 使用迁移学习进行金融小样本风控实践（基于tradaboost进行个贷违约迁移学习比赛）
 消费金融大数据风控架构
 使用迁移学习进行金融小样本风控实践（基于tradaboost进行个贷违约迁移学习比赛）---- 代码

id	Field	Description
1	id	为贷款清单分配的唯一信用证标识
2	loanAmnt	贷款金额
3	term	贷款期限（year）
4	interestRate	贷款利率
5	installment	分期付款金额
6	grade	贷款等级
7	subGrade	贷款等级之子级
8	employmentTitle	就业职称
9	employmentLength	就业年限（年）
10	homeOwnership	借款人在登记时提供的房屋所有权状况
11	annualIncome	年收入
12	verificationStatus	验证状态
13	issueDate	贷款发放的月份
14	purpose	借款人在贷款申请时的贷款用途类别
15	postCode	借款人在贷款申请中提供的邮政编码的前3位数字
16	regionCode	地区编码
17	dti	债务收入比
18	delinquency_2years	借款人过去2年信用档案中逾期30天以上的违约事件数
19	ficoRangeLow	借款人在贷款发放时的fico所属的下限范围
20	ficoRangeHigh	借款人在贷款发放时的fico所属的上限范围
21	openAcc	借款人信用档案中未结信用额度的数量
22	pubRec	贬损公共记录的数量
23	pubRecBankruptcies	公开记录清除的数量
24	revolBal	信贷周转余额合计
25	revolUtil	循环额度利用率，或借款人使用的相对于所有可用循环信贷的信贷金额
26	totalAcc	借款人信用档案中当前的信用额度总数
27	initialListStatus	贷款的初始列表状态
28	applicationType	表明贷款是个人申请还是与两个共同借款人的联合申请
29	earliesCreditLine	借款人最早报告的信用额度开立的月份
30	title	借款人提供的贷款名称
31	policyCode	公开可用的策略_代码=1新产品不公开可用的策略_代码=2
32	n系列匿名特征	匿名特征n0-n14，为一些贷款人行为计数特征的处理

数据挖掘实践（金融风控）：金融风控之贷款违约预测挑战赛（下篇）[xgboots/lightgbm/Catboost等模型]--模型融合：stackingblending

数据挖掘实践（金融风控）：金融风控之贷款违约预测挑战赛（下篇）[xgboots/lightgbm/Catboost等模型]--模型融合：stacking、blending

4.建模与调参

项目链接以及码源见文末

4.1 模型对比与性能评估

4.1.1 逻辑回归

4.1.2 决策树模型

4.1.3 集成模型集成方法（ensemble method）

4.1.4 模型评估方法

4.1.5 模型评价标准

4.2代码实战

4.2.1 简单建模

4.2.2 模型调参（贪心、网格搜索、贝叶斯）

贪心调参

网格搜索

贝叶斯调参

4.3 模型调参小总结**

4.4 模型相关原理介绍

4.4.1 逻辑回归模型

4.4.2 决策树模型

4.4.3 GBDT模型

4.4.4 XGBoost模型

4.4.5 LightGBM模型

4.4.6 Catboost模型

4.4.7 时间序列模型(选学)

5.模型融合

5.1 stacking\\blending详解

5.1.1 平均：

5.1.2 投票

5.1.3 Stacking：

5.1.2 blending

5.2 小结总结

6.完整baseline代码

6.1数据预处理

6.2训练数据/测试数据准备

6.3模型训练

零基础入门金融风控-贷款违约预测-机器学习-数据分析

零基础入门金融风控-贷款违约预测

一、赛题数据

二、评测标准

三、代码演示

1. 数据分析及处理

1.1.0导入相关库

1.1.1数据预处理

1.1.2数值型变量和非数值型变量的处理与分析

1.1.3数值型(numeric_cols)测试集与训练集分布

1.1.4取出数值连续性变量，查看数据分布

1.1.5查看数值非连续性型数据分布

1.1.6查看非数值型数据分布

2. 特征工程

2.1.1 数值非连续性型数据处理

2.1.2 非数值型数据

3. 保存文件

4. 数据建模

4.1.1数据查看

4.1.1选择算法