FM算法解析及Python实现

Posted 2021-01-04 Bo_hemian

1. 什么是FM？

FM即Factor Machine，因子分解机。

2. 为什么需要FM？

1、特征组合是许多机器学习建模过程中遇到的问题，如果对特征直接建模，很有可能会忽略掉特征与特征之间的关联信息，因此，可以通过构建新的交叉特征这一特征组合方式提高模型的效果。

2、高维的稀疏矩阵是实际工程中常见的问题，并直接会导致计算量过大，特征权值更新缓慢。试想一个10000*100的表，每一列都有8种元素，经过one-hot独热编码之后，会产生一个10000*800的表。因此表中每行元素只有100个值为1，700个值为0。

而FM的优势就在于对这两方面问题的处理。首先是特征组合，通过对两两特征组合，引入交叉项特征，提高模型得分；其次是高维灾难，通过引入隐向量（对参数矩阵进行矩阵分解），完成对特征的参数估计。

3. FM用在哪？

我们已经知道了FM可以解决特征组合以及高维稀疏矩阵问题，而实际业务场景中，电商、豆瓣等推荐系统的场景是使用最广的领域，打个比方，小王只在豆瓣上浏览过20部电影，而豆瓣上面有20000部电影，如果构建一个基于小王的电影矩阵，毫无疑问，里面将有199980个元素全为0。而类似于这样的问题就可以通过FM来解决。

4. FM长什么样？

在展示FM算法前，我们先回顾一下最常见的线性表达式：

其中w₀ 为初始权值，或者理解为偏置项，w_i 为每个特征x_i 对应的权值。可以看到，这种线性表达式只描述了每个特征与输出的关系。

FM的表达式如下，可观察到，只是在线性表达式后面加入了新的交叉项特征及对应的权值。

5. FM交叉项的展开

5.1 寻找交叉项

FM表达式的求解核心在于对交叉项的求解。下面是很多人用来求解交叉项的展开式，对于第一次接触FM算法的人来说可能会有疑惑，不知道公式怎么展开的，接下来笔者会手动推导一遍。

设有3个变量（特征）x1 x2 x3，每一个特征的隐变量分别为v1=(1 2 3)、v2=(4 5 6)、v3=(1 2 1)，即：

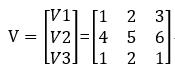
设交叉项所组成的权矩阵W为对称矩阵，之所以设为对称矩阵是因为对称矩阵有可以用向量乘以向量转置替代的性质。
那么W=VV^T，即

所以：

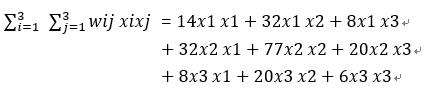
实际上，我们应该考虑的交叉项应该是排除自身组合的项，即对于x1x1、x2x2、x3x3不认为是交叉项，那么真正的交叉项为x1x2、x1x3、x2x1、x2x3、x3x1、x3x2。
去重后，交叉项即x1x2、x1x3、x2x3。这也是公式中1/2出现的原因。

5.2 交叉项权值转换

对交叉项有了基本了解后，下面将进行公式的分解，还是以n=3为例，

所以：

wij可记作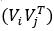或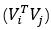，这取决于vi是1*3 还是3*1 向量。

 5.3 交叉项展开式

上面的例子是对3个特征做的交叉项推导，因此对具有n个特征，FM的交叉项公式就可推广为：

 

我们还可以进一步分解：

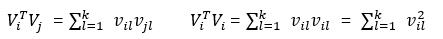
所以FM算法的交叉项最终可展开为：

5.4 隐向量v就是embedding vector?

假设训练数据集dataMatrix的shape为（20000，9)，取其中一行数据作为一条样本i，那么样本i 的shape为（1，9），同时假设隐向量vi的shape为（9，8）（注：8为自定义值，代表embedding vector的长度）

所以5.3小节中的交叉项可以表示为：

sum((inter_1)^2 - (inter_2)^2)/2

其中：

inter_1 = i*v  shape为（1，8）

inter_2 = np.multiply(i)*np.multiply(v)  shape为（1，8）

可以看到，样本i 经过交叉项中的计算后，得到向量shape为（1，8）的inter_1和 inter_2。

由于维度变低，所以此计算过程可以近似认为在交叉项中对样本i 进行了embedding vector转换。

故，我们需要对之前的理解进行修正：

1. 我们口中的隐向量vi实际上是一个向量组，其形状为（输入特征One-hot后的长度，自定义长度）；
2. 隐向量vi代表的并不是embedding vector，而是在对输入进行embedding vector的向量组，也可理解为是一个权矩阵；
3. 由输入i*vi得到的向量才是真正的embedding vector。

具体可以结合第7节点的代码实现进行理解。

6. 权值求解

利用梯度下降法，通过求损失函数对特征（输入项）的导数计算出梯度，从而更新权值。设m为样本个数，θ为权值。

如果是回归问题，损失函数一般是均方误差（MSE）:

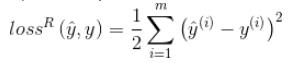
所以回归问题的损失函数对权值的梯度（导数）为：

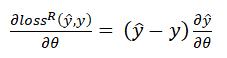
如果是二分类问题，损失函数一般是logit loss：

其中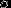，表示的是阶跃函数Sigmoid。

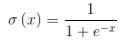
所以分类问题的损失函数对权值的梯度（导数）为：

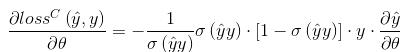
 相应的，对于常数项、一次项、交叉项的导数分别为:

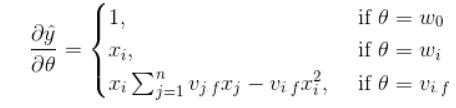
7. FM算法的Python实现

 FM算法的Python实现流程图如下：

 

我们需要注意以下四点：

1. 初始化参数，包括对偏置项权值w0、一次项权值w以及交叉项辅助向量的初始化；

2. 定义FM算法；

3. 损失函数梯度的定义；

4. 利用梯度下降更新参数。

下面的代码片段是以上四点的描述，其中的loss并不是二分类的损失loss，而是分类loss的梯度中的一部分：

loss = self.sigmoid(classLabels[x] * p[0, 0]) -1

实际上，二分类的损失loss的梯度可以表示为：

gradient = (self.sigmoid(classLabels[x] * p[0, 0]) -1)*classLabels[x]*p_derivative

其中 p_derivative 代表常数项、一次项、交叉项的导数（详见本文第6小节）。

FM算法代码片段

 1         # 初始化参数
 2         w = zeros((n, 1))  # 其中n是特征的个数
 3         w_0 = 0.
 4         v = normalvariate(0, 0.2) * ones((n, k))
 5         for it in range(self.iter): # 迭代次数
 6             # 对每一个样本，优化
 7             for x in range(m):
 8                 # 这边注意一个数学知识：对应点积的地方通常会有sum，对应位置积的地方通常都没有，详细参见矩阵运算规则，本处计算逻辑在：http://blog.csdn.net/google19890102/article/details/45532745
 9                 # xi·vi,xi与vi的矩阵点积
10                 inter_1 = dataMatrix[x] * v
11                 # xi与xi的对应位置乘积   与   xi^2与vi^2对应位置的乘积    的点积
12                 inter_2 = multiply(dataMatrix[x], dataMatrix[x]) * multiply(v, v)  # multiply对应元素相乘
13                 # 完成交叉项,xi*vi*xi*vi - xi^2*vi^2
14                 interaction = sum(multiply(inter_1, inter_1) - inter_2) / 2.
15                 # 计算预测的输出
16                 p = w_0 + dataMatrix[x] * w + interaction
17                 print(\'classLabels[x]:\',classLabels[x])
18                 print(\'预测的输出p:\', p)
19                 # 计算sigmoid(y*pred_y)-1准确的说不是loss，原作者这边理解的有问题，只是作为更新w的中间参数，这边算出来的是越大越好，而下面却用了梯度下降而不是梯度上升的算法在
20                 loss = self.sigmoid(classLabels[x] * p[0, 0]) - 1
21                 if loss >= -1:
22                     loss_res = \'正方向 \'
23                 else:
24                     loss_res = \'反方向\'
25                 # 更新参数
26                 w_0 = w_0 - self.alpha * loss * classLabels[x]
27                 for i in range(n):
28                     if dataMatrix[x, i] != 0:
29                         w[i, 0] = w[i, 0] - self.alpha * loss * classLabels[x] * dataMatrix[x, i]
30                         for j in range(k):
31                             v[i, j] = v[i, j] - self.alpha * loss * classLabels[x] * (
32                                     dataMatrix[x, i] * inter_1[0, j] - v[i, j] * dataMatrix[x, i] * dataMatrix[x, i])

 

FM算法完整实现

  1 # -*- coding: utf-8 -*-
  2 
  3 from __future__ import division
  4 from math import exp
  5 from numpy import *
  6 from random import normalvariate  # 正态分布
  7 from sklearn import preprocessing
  8 import numpy as np
  9 
 10 \'\'\'
 11     data : 数据的路径
 12     feature_potenital : 潜在分解维度数
 13     alpha ： 学习速率
 14     iter ： 迭代次数
 15     _w,_w_0,_v ： 拆分子矩阵的weight
 16     with_col : 是否带有columns_name
 17     first_col : 首列有价值的feature的index
 18 \'\'\'
 19 
 20 
 21 class fm(object):
 22     def __init__(self):
 23         self.data = None
 24         self.feature_potential = None
 25         self.alpha = None
 26         self.iter = None
 27         self._w = None
 28         self._w_0 = None
 29         self.v = None
 30         self.with_col = None
 31         self.first_col = None
 32 
 33     def min_max(self, data):
 34         self.data = data
 35         min_max_scaler = preprocessing.MinMaxScaler()
 36         return min_max_scaler.fit_transform(self.data)
 37 
 38     def loadDataSet(self, data, with_col=True, first_col=2):
 39         # 我就是闲的蛋疼，明明pd.read_table()可以直接度，非要搞这样的，显得代码很长，小数据下完全可以直接读嘛，唉～
 40         self.first_col = first_col
 41         dataMat = []
 42         labelMat = []
 43         fr = open(data)
 44         self.with_col = with_col
 45         if self.with_col:
 46             N = 0
 47             for line in fr.readlines():
 48                 # N=1时干掉列表名
 49                 if N > 0:
 50                     currLine = line.strip().split()
 51                     lineArr = []
 52                     featureNum = len(currLine)
 53                     for i in range(self.first_col, featureNum):
 54                         lineArr.append(float(currLine[i]))
 55                     dataMat.append(lineArr)
 56                     labelMat.append(float(currLine[1]) * 2 - 1)
 57                 N = N + 1
 58         else:
 59             for line in fr.readlines():
 60                 currLine = line.strip().split()
 61                 lineArr = []
 62                 featureNum = len(currLine)
 63                 for i in range(2, featureNum):
 64                     lineArr.append(float(currLine[i]))
 65                 dataMat.append(lineArr)
 66                 labelMat.append(float(currLine[1]) * 2 - 1)
 67         return mat(self.min_max(dataMat)), labelMat
 68 
 69     def sigmoid(self, inx):
 70         # return 1.0/(1+exp(min(max(-inx,-10),10)))
 71         return 1.0 / (1 + exp(-inx))
 72 
 73     # 得到对应的特征weight的矩阵
 74     def fit(self, data, feature_potential=8, alpha=0.01, iter=100):
 75         # alpha是学习速率
 76         self.alpha = alpha
 77         self.feature_potential = feature_potential
 78         self.iter = iter
 79         # dataMatrix用的是mat, classLabels是列表
 80         dataMatrix, classLabels = self.loadDataSet(data)
 81         print(\'dataMatrix:\',dataMatrix.shape)
 82         print(\'classLabels:\',classLabels)
 83         k = self.feature_potential
 84         m, n = shape(dataMatrix)
 85         # 初始化参数
 86         w = zeros((n, 1))  # 其中n是特征的个数
 87         w_0 = 0.
 88         v = normalvariate(0, 0.2) * ones((n, k))
 89         for it in range(self.iter): # 迭代次数
 90             # 对每一个样本，优化
 91             for x in range(m):
 92                 # 这边注意一个数学知识：对应点积的地方通常会有sum，对应位置积的地方通常都没有，详细参见矩阵运算规则，本处计算逻辑在：http://blog.csdn.net/google19890102/article/details/45532745
 93                 # xi·vi,xi与vi的矩阵点积
 94                 inter_1 = dataMatrix[x] * v
 95                 # xi与xi的对应位置乘积   与   xi^2与vi^2对应位置的乘积    的点积
 96                 inter_2 = multiply(dataMatrix[x], dataMatrix[x]) * multiply(v, v)  # multiply对应元素相乘
 97                 # 完成交叉项,xi*vi*xi*vi - xi^2*vi^2
 98                 interaction = sum(multiply(inter_1, inter_1) - inter_2) / 2.
 99                 # 计算预测的输出
100                 p = w_0 + dataMatrix[x] * w + interaction
101                 print(\'classLabels[x]:\',classLabels[x])
102                 print(\'预测的输出p:\', p)
103                 # 计算sigmoid(y*pred_y)-1
104                 loss = self.sigmoid(classLabels[x] * p[0, 0]) - 1
105                 if loss >= -1:
106                     loss_res = \'正方向 \'
107                 else:
108                     loss_res = \'反方向\'
109                 # 更新参数
110                 w_0 = w_0 - self.alpha * loss * classLabels[x]
111                 for i in range(n):
112                     if dataMatrix[x, i] != 0:
113                         w[i, 0] = w[i, 0] - self.alpha * loss * classLabels[x] * dataMatrix[x, i]
114                         for j in range(k):
115                             v[i, j] = v[i, j] - self.alpha * loss * classLabels[x] * (
116                                     dataMatrix[x, i] * inter_1[0, j] - v[i, j] * dataMatrix[x, i] * dataMatrix[x, i])
117             print(\'the no %s times, the loss arrach %s\' % (it, loss_res))
118         self._w_0, self._w, self._v = w_0, w, v
119 
120     def predict(self, X):
121         if (self._w_0 == None) or (self._w == None).any() or (self._v == None).any():
122             raise NotFittedError("Estimator not fitted, call `fit` first")
123         # 类型检查
124         if isinstance(X, np.ndarray):
125             pass
126         else:
127             try:
128                 X = np.array(X)
129             except:
130                 raise TypeError("numpy.ndarray required for X")
131         w_0 = self._w_0
132         w = self._w
133         v = self._v
134         m, n = shape(X)
135         result = []
136         for x in range(m):
137             inter_1 = mat(X[x]) * v
138             inter_2 = mat(multiply(X[x], X[x])) * multiply(v, v)  # multiply对应元素相乘
139             # 完成交叉项
140             interaction = sum(multiply(inter_1, inter_1) - inter_2) / 2.
141             p = w_0 + X[x] * w + interaction  # 计算预测的输出
142             pre = self.sigmoid(p[0, 0])
143             result.append(pre)
144         return result
145 
146     def getAccuracy(self, data):
147         dataMatrix, classLabels = self.loadDataSet(data)
148         w_0 = self._w_0
149         w = self._w
150         v = self._v
151         m, n = shape(dataMatrix)
152         allItem = 0
153         error = 0
154         result = []
155         for x in range(m):
156             allItem += 1
157             inter_1 = dataMatrix[x] * v
158             inter_2 = multiply(dataMatrix[x], dataMatrix[x]) * multiply(v, v)  # multiply对应元素相乘
159             # 完成交叉项
160             interaction = sum(multiply(inter_1, inter_1) - inter_2) / 2.
161             p = w_0 + dataMatrix[x] * w + interaction  # 计算预测的输出
162             pre = self.sigmoid(p[0, 0])
163             result.append(pre)
164             if pre < 0.5 and classLabels[x] == 1.0:
165                 error += 1
166             elif pre >= 0.5 and classLabels[x] == -1.0:
167                 error += 1
168             else:
169                 continue
170         # print(result)
171         value = 1 - float(error) / allItem
172         return value
173 
174 
175 class NotFittedError(Exception):
176     """
177     Exception class to raise if estimator is used before fitting
178     """
179     pass
180 
181 
182 if __name__ == \'__main__\':
183     fm()

 

=