Python LDA降维中不能输出指定维度（n_components）的新数据集

Posted 2023-05-08

#LDA降维
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis
lda = LinearDiscriminantAnalysis(n_components=30)
lda.fit(X_1,y_1)
X_new_1 = lda.transform(X_1)

可以看到我已经把n_components设为30时了，但最后输出的X_new_1还是降到只有一个属性，请问这是什么原因？

LDA降维后的维度区间在[1,C-1]，C为特征空间的维度，与原始特征数n无关，对于二值分类，最多投影到1维，所以我估计你是因为这是个二分类问题，所以只能降到一维。 参考技术A 首先2个包：

import numpy as npfrom sklearn.decomposition import PCA

然后一个m x n 的矩阵，n为维度，这里设为x。
n_components = 12 是自己可以设的。

pca = PCA(n_components=12)pca.fit(x)PCA(copy=True, iterated_power='auto', n_components=12, random_state=None, svd_solver='auto', tol=0.0, whiten=False) float_formatter = lambda x: "%.2f" % xnp.set_printoptions(formatter='float_kind':float_formatter) print 'explained variance ratio:'print pca.explained_variance_ratio_print 'cumulative sum:'print pca.explained_variance_ratio_.cumsum() 参考技术B n_components注意只能为[1,类别数-1)范围之间的整数，是类别数-1，而不是特征数-1 参考技术C 必须满足：n_components<=n_classes-1，n_classes是类别数 参考技术D 我也遇到了这个问题，请问楼主解决了吗？

模式识别实验一：Fisher线性判别（LDA）

Fisher线性判别也叫作LDA，它可用于降维也可用于分类，当维度降低成1维时，确定一个阈值，即可实现分类。和PCA相比，LDA是一种有监督的降维算法，局限性在于降低的维度必须小于样本类别数-1。LDA分类的核心思想是将样本的向量空间投射到一个一维直线上，使样本类内离散度尽可能小，类间离散度尽可能大。本实验通过sonar和Iris数据集，实现了三种不同方式的分类算法，并在sonar数据集上选取了部分特征，考察了特征数和分类精确度之间的关系。
pdf版的实验报告可以戳这：https://download.csdn.net/download/qq1198768105/34257333
sonar和Iris数据集下载可以戳这：https://download.csdn.net/download/qq1198768105/31613770

实验报告图片版

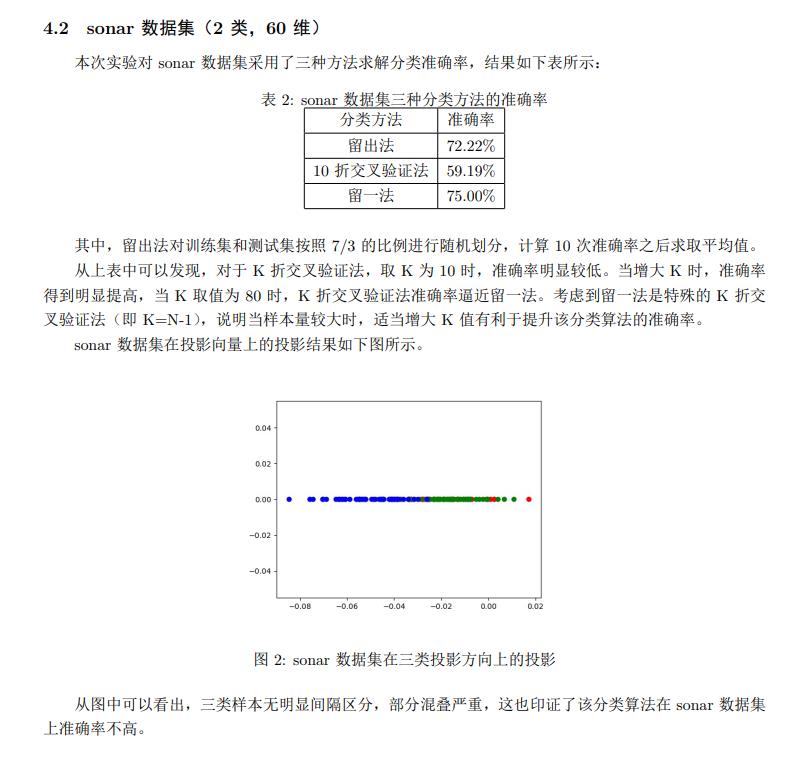
程序代码

sonar数据集分类

import numpy as np
from sklearn.model_selection import train_test_split, KFold, LeaveOneOut
import matplotlib.pyplot as plt


# 正常导入数据
def load_dataset():
    data = np.genfromtxt('sonar.txt', delimiter=',', usecols=np.arange(0, 60))
    target = np.genfromtxt('sonar.txt', delimiter=',', usecols=(60), dtype=str)
    t = np.zeros(len(target))
    t[target == 'R'] = 1
    t[target == 'M'] = 2
    return data, t


# 自定义导入数据维度
def load_dataset_dimension(dimension):
    data = np.genfromtxt('sonar.txt', delimiter=',', usecols=np.arange(0, dimension))
    target = np.genfromtxt('sonar.txt', delimiter=',', usecols=(60), dtype=str)
    t = np.zeros(len(target))
    t[target == 'R'] = 1
    t[target == 'M'] = 2
    return data, t


def fisher(class1, class2):
    class1 = np.mat(class1)
    class2 = np.mat(class2)

    # 求解每一个特征的均值，按列求解
    a1 = np.mean(class1, axis=0)
    a2 = np.mean(class2, axis=0)

    # 直接代入公式求解类内离散度矩阵
    s1 = (class1 - a1).T * (class1 - a1)
    s2 = (class2 - a2).T * (class2 - a1)
    sw = s1 + s2
    # 这里是求解离散度矩阵的另一种思路：通过协方差公式求解，49为样本数量-1(n-1)
    # s = np.cov(class0.T) * 49

    # w 为最佳变换向量w*，w0为阈值
    w = (a1 - a2) * np.linalg.inv(sw)
    w0 = (a1 * w.T + a2 * w.T) / 2
    return w, w0


# 计算分类准确率
def accuracy(pre, tar):
    total = len(pre)
    acc = 0
    for i in range(total):
        if pre[i] == tar[i]:
            acc += 1
    return acc / total


# 修改两个类别标签
def transform_target(data, target):
    class1 = []
    class2 = []
    for i in range(len(data)):
        if target[i] == 1:
            class1.append(data[i])
        elif target[i] == 2:
            class2.append(data[i])
    return class1, class2


# method1 留出法，随机划分训练测试集，多次平均求结果
def method1():
    data, target = load_dataset()

    # 使用留出法随机划分数据集，训练集/测试集=7/3, 每次划分具有随机性
    X_train, X_test, Y_train, Y_test = train_test_split(data, target, test_size=0.30)

    class1, class2 = transform_target(X_train, Y_train)
    # w代表投影向量，w0代表第一类和第二类比较时的阈值。
    w, w0 = fisher(class1, class2)

    y = X_test * w.T
    res = np.zeros(len(X_test))
    for i in range(len(res)):
        if y[i] > w0:
            res[i] = 1
        else:
            res[i] = 2
    # print(res)
    acc = accuracy(res, Y_test)
    # print("分类准确率为", acc)
    return acc


# method2 k折交叉验证法
def method2():
    data, target = load_dataset()
    acc = 0
    K = 10  # 这里设定k为10
    kf = KFold(n_splits=K)
    for train_index, test_index in kf.split(data):
        X_train = data[train_index]
        X_test = data[test_index]
        Y_train = target[train_index]
        Y_test = target[test_index]
        class1, class2 = transform_target(X_train, Y_train)
        # w代表投影向量，w0代表第一类和第二类比较时的阈值。
        w, w0 = fisher(class1, class2)

        y = X_test * w.T
        res = np.zeros(len(X_test))
        for i in range(len(res)):
            if y[i] > w0:
                res[i] = 1
            else:
                res[i] = 2
        # print(res)
        acc += accuracy(res, Y_test)
        # print("分类准确率为", acc)
    acc = acc / K
    return acc


# method3 留一法
def method3():
    data, target = load_dataset()
    loo = LeaveOneOut()
    acc = 0
    for train_index, test_index in loo.split(data):
        X_train = data[train_index]
        X_test = data[test_index]
        Y_train = target[train_index]
        Y_test = target[test_index]
        class1, class2 = transform_target(X_train, Y_train)
        # w代表投影向量，w0代表第一类和第二类比较时的阈值。
        w, w0 = fisher(class1, class2)

        y = X_test * w.T
        res = np.zeros(len(X_test))
        for i in range(len(res)):
            if y[i] > w0:
                res[i] = 1
            else:
                res[i] = 2
        # print(res)
        acc += accuracy(res, Y_test)
        # print("分类准确率为", acc)
    acc = acc / len(data)
    return acc


# dension 以留一法为基础，测试维度和准确率的关系
def dension(dimension):
    data, target = load_dataset_dimension(dimension)
    loo = LeaveOneOut()
    acc = 0
    for train_index, test_index in loo.split(data):
        X_train = data[train_index]
        X_test = data[test_index]
        Y_train = target[train_index]
        Y_test = target[test_index]
        class1, class2 = transform_target(X_train, Y_train)
        # w代表投影向量，w0代表第一类和第二类比较时的阈值。
        w, w0 = fisher(class1, class2)

        y = X_test * w.T
        res = np.zeros(len(X_test))
        for i in range(len(res)):
            if y[i] > w0:
                res[i] = 1
            else:
                res[i] = 2
        # print(res)
        acc += accuracy(res, Y_test)
        # print("分类准确率为", acc)
    acc = acc / len(data)
    return acc


# 绘制投影图
def draw():
    data, target = load_dataset()
    class1, class2 = transform_target(data, target)

    w, w0 = fisher(class1, class2)
    y = data * w.T

    plt.figure(1)
    plt.plot(y[0:49], np.zeros([49, 1]), 'ro')
    plt.plot(y[50:99], np.zeros([49, 1]), 'go')
    plt.plot(y[100:149], np.zeros([49, 1]), 'bo')
    plt.savefig('./sonar.jpg')
    plt.show()


def main():
    # 10次计算方法一的留出法，取平均准确率作为结果(保留两位小数输出)
    total_accuary1 = 0
    for i in range(10):
        total_accuary1 += method1()
    total_accuary1 = total_accuary1 / 10
    print("留出法的分类准确率为：", "{:.2%}".format(total_accuary1))
    # draw()
    total_accuary2 = method2()
    print("K折交叉验证法的分类准确率为：", "{:.2%}".format(total_accuary2))
    total_accuary3 = method3()
    print("留一法的分类准确率为：", "{:.2%}".format(total_accuary3))


    # 绘制维度与准确率的关系图
    total_accuary = []
    plt.figure(2)
    for demension in range(2, 60):
        total_accuary.append(dension(demension))
    print(total_accuary)
    plt.plot(np.arange(2, 60), total_accuary)
    # 解决中文显示问题
    plt.rcParams['font.sans-serif'] = ['SimHei']
    plt.rcParams['axes.unicode_minus'] = False
    plt.xlabel("维度")
    plt.ylabel("准确率")
    plt.title("sonar数据集准确率随维度的变化图（留一法）")
    plt.savefig('./demension.jpg')
    plt.show()



if __name__ == '__main__':
    main()

Iris数据集分类

import numpy as np
from sklearn.model_selection import train_test_split, KFold, LeaveOneOut
import matplotlib.pyplot as plt


def load_dataset():
    data = np.genfromtxt('iris.txt', delimiter=',', usecols=(0, 1, 2, 3))
    target = np.genfromtxt('iris.txt', delimiter=',', usecols=(4), dtype=str)
    t = np.zeros(len(target))
    t[target == 'setosa'] = 1
    t[target == 'versicolor'] = 2
    t[target == 'virginica'] = 3
    return data, t


def fisher(class1, class2):
    class1 = np.mat(class1)
    class2 = np.mat(class2)

    # 求解每一个特征的均值，按列求解
    a1 = np.mean(class1, axis=0)
    a2 = np.mean(class2, axis=0)

    # 直接代入公式求解类内离散度矩阵
    s1 = (class1 - a1).T * (class1 - a1)
    s2 = (class2 - a2).T * (class2 - a1)
    sw = s1 + s2
    # 这里是求解离散度矩阵的另一种思路：通过协方差公式求解，49为样本数量-1(n-1)
    # s = np.cov(class0.T) * 49

    # w 为最佳变换向量w*，w0为阈值
    w = (a1 - a2) * np.linalg.inv(sw)
    w0 = (a1 * w.T + a2 * w.T) / 2
    return w, w0


# 计算分类准确率
def accuracy(pre, tar):
    total = len(pre)
    acc = 0
    for i in range(total):
        if pre[i] == tar[i]:
            acc += 1
    return acc / total


# 修改三个类别标签
def transform_target(data, target):
    class1 = []
    class2 = []
    class3 = []
    for i in range(len(data)):
        if target[i] == 1:
            class1.append(data[i])
        elif target[i] == 2:
            class2.append(data[i])
        else:
            class3.append(data[i])
    return class1, class2, class3


# method1 留出法，随机划分训练测试集，多次平均求结果
def method1():
    data, target = load_dataset()

    # 使用留出法随机划分数据集，训练集/测试集=7/3, 每次划分具有随机性
    X_train, X_test, Y_train, Y_test = train_test_split(data, target, test_size=0.30)

    class1, class2, class3 = transform_target(X_train, Y_train)
    # w12代表第一类和第二类比较的投影向量，w012代表第一类和第二类比较时的阈值，其它同理。
    w12, w012 = fisher(class1, class2)
    w13, w013 = fisher(class1, class3)
    w23, w023 = fisher(class2, class3)

    # 3分类的比较思路：两两进行比较，若两次均分类正确才算正确
    y12 = X_test * w12.T
    y13 = X_test * w13.T
    y23 = X_test * w23.T
    res = np.zeros(len(X_test))
    for i in range(len(res)):
        if y12[i] > w012 and y12[i] > w013:
            res[i] = 1
        if y12[i] < w012 and y23[i] > w023:
            res[i] = 2
        if y13[i] < w013 and y23[i] < w023:
            res[i] = 3
    # print(res)
    acc = accuracy(res, Y_test)
    # print("分类准确率为", acc)
    return acc


# method2 k折交叉验证法
def method2():
    data, target = load_dataset()
    acc = 0
    K = 10  # 这里设定k为10
    kf = KFold(n_splits=K)
    for train_index, test_index in kf.split(data):
        X_train = data[train_index]
        X_test = data[test_index]
        Y_train = target[train_index]
        Y_test = target[test_index]
        class1, class2, class3 = transform_target(X_train, Y_train)
        # w12代表第一类和第二类比较的投影向量，w012代表第一类和第二类比较时的阈值，其它同理。
        w12, w012 = fisher(class1, class2)
        w13, w013 = fisher(class1, class3)
        w23, w023 = fisher(class2, class3)

        # 3分类的比较思路：两两进行比较，若两次均分类正确才算正确
        y12 = X_test * w12.T
        y13 = X_test * w13.T
        y23 = X_test * w23.T
        res = np.zeros(len(X_test))
        for i in range(len(res)):
            if y12[i] > w012 and y12[i] > w013:
                res[i] = 1
            if y12[i] < w012 and y23[i] > w023:
                res[i] = 2
            if y13[i] < w013 and y23[i] < w023:
                res[i] = 3
        # print(res)
        acc += accuracy(res, Y_test)
        # print("分类准确率为", acc)
    acc = acc / K
    return acc

# method3 留一法
def method3():
    data, target = load_dataset()
    loo = LeaveOneOut()
    acc = 0
    for train_index, test_index in loo.以上是关于Python LDA降维中不能输出指定维度（n_components）的新数据集的主要内容，如果未能解决你的问题，请参考以下文章
 
 LDA和PCA降维的原理和区别
 常用降维方法之PCA 和 LDA
 LDA线性模型
 PCA（主成分分析）+LDA（线性判别分析）+区别
 LAD线性判别模型简介及sklearn参数
 线性差别分析LDA