遗传算法的中心思想

Posted 2023-05-04

ＲＴ

遗传算法是通过大量备选解的变换、迭代和变异，在解空间中并行动态地进行全局搜索的最优化方法，由于遗传算法具有比较完备的数学模型和理论，在解决很多NP—Hard问题上具有良好的性能。

遗传算法以一种群体中的所有个体为对象，并利用随机化技术指导对一个被编码的参数空间进行高效搜索。其中选择、交叉和变异构成了遗传算法的遗传操作，参数编码、初始群体的设定、适应度函数的设计、遗传操作设计、控制参数设定五个要素组成了遗传算法的核心内容。

扩展资料：

遗传算法注意事项：

用户需要注意遗传算法的优化过程中种群基因的多样性是保障避免陷入局部最优解的重要因素，如果目标函数优化结果过早收敛很可能就是因为种群的多样性不足。

为了保证种群的多样性，其中编码、适应度函数设计尤为重要。

适应度的含义就是字面意思，这个个体是否可以适应环境也即是否满足优化目标指标。因为后续需要根据适应度函数进行自然选择，因此适应度函数和你的目标函数并不需要完全一样。

参考资料来源：百度百科-遗传算法

参考技术A 遗传算法的中心思想就是对一定数量个体组成的生物种群进行选择、交叉、变异等遗传操作,最终求得最优解或近似最优解。在进行遗传操作时,几个重要的参数为:染色体长度L,种群大小M,交叉概率Pc,变异概率Pm,终止代数T。

matlab遗传算法多配送中心路径优化（带时间窗）

clear
clc
close all
tic
%% 用importdata这个函数来读取文件
% shuju=importdata('cc101.txt');
load('cc101');
shuju=c101;
% bl=importdata('103.txt');
bl=3;
cap=60;                                                        %车辆最大装载量
%% 提取数据信息

E=shuju(1,5);                                                    %配送中心时间窗开始时间
L=shuju(1,6);                                                    %配送中心时间窗结束时间
zuobiao=shuju(:,2:3);                                       %所有点的坐标x和y
pszx=zuobiao(1:4,:);
customer=zuobiao(5:end,:);                                       %顾客坐标
cusnum=size(customer,1);                                         %顾客数
v_num=20;                                                        %车辆最多使用数目
demands=shuju(5:end,4);                                          %需求量
a=shuju(5:end,5);                                                %顾客时间窗开始时间[a[i],b[i]]
b=shuju(5:end,6);                                                %顾客时间窗结束时间[a[i],b[i]]
s=shuju(5:end,7);                                                %客户点的服务时间
h=pdist(zuobiao);
dist=squareform(h);    
% dist=load('dist.mat');
% dist=struct2cell(dist);
% dist=cell2mat(dist);
dist=dist./1000;%距离矩阵，满足三角关系，暂用距离表示花费c[i][j]=dist[i][j]
%% 遗传算法参数设置
alpha=100000;                                                       %违反的容量约束的惩罚函数系数
belta=90;%违反时间窗约束的惩罚函数系数
belta2=60;
chesu=20;

NIND=300;                                                       %种群大小
MAXGEN=1000;                                                     %迭代次数
Pc=0.9;                                                         %交叉概率
Pm=0.05;                                                        %变异概率
GGAP=0.9;                                                       %代沟(Generation gap)
N=cusnum+v_num-1;                                %染色体长度=顾客数目+车辆最多使用数目-1
% N=cusnum;
%% 初始化种群
% init_vc=init(cusnum,a,demands,cap); 
dpszx = struct('ps',[], 'Chrom',[]);
dpszx.Chrom=InitPopCW(NIND,N,cusnum,a,demands,cap);     %构造初始解
ps=pszxxz(dpszx.Chrom,cusnum);
%% 输出随机解的路线和总距离
disp('初始种群中的一个随机值:')

 [VC,NV,TD,violate_num,violate_cus]=decode(dpszx.Chrom(1,:),cusnum,cap,demands,a,b,L,s,dist,chesu,bl);
% [VC,NV]=cls(dpszx.Chrom(1,:),cusnum);
    
% [~,~,bsv]=violateTW(VC,a,b,s,L,dist,chesu,bl);
% disp(['总距离：',num2str(TD)]);
disp(['车辆使用数目：',num2str(NV),'，车辆行驶总距离：',num2str(TD)]);
disp('~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~')
%% 优化
gen=1;
figure;
hold on;box on
xlim([0,MAXGEN])
title('优化过程')
xlabel('代数')
ylabel('最优值')
ObjV=calObj(dpszx.Chrom,cusnum,cap,demands,a,b,L,s,dist,alpha,belta,belta2,chesu,bl,ps);             %计算种群目标函数值
preObjV=min(ObjV);
%%
while gen<=MAXGEN
    %% 计算适应度
    ObjV=calObj(dpszx.Chrom,cusnum,cap,demands,a,b,L,s,dist,alpha,belta,belta2,chesu,bl,ps);             %计算种群目标函数值
    line([gen-1,gen],[preObjV,min(ObjV)]);pause(0.0001)%画图 最优函数
    preObjV=min(ObjV);
    FitnV=Fitness(ObjV);
    %% 选择
    [SelCh,psc]=Select(dpszx.Chrom,FitnV,GGAP,ps);
    %% OX交叉操作
    [SelCh,psc]=Recombin(SelCh,Pc,psc,cusnum);
    %% 变异
    [SelCh,psc]=Mutate(SelCh,Pm,psc,cusnum);
    %% 重插入子代的新种群
    [dpszx.Chrom,ps]=Reins(dpszx.Chrom,SelCh,ObjV,psc,ps);
    %% 打印当前最优解
    ObjV=calObj(dpszx.Chrom,cusnum,cap,demands,a,b,L,s,dist,alpha,belta,belta2,chesu,bl,ps);             %计算种群目标函数值
    [minObjV,minInd]=min(ObjV);
    disp(['第',num2str(gen),'代最优解:'])
    [bestVC,bestNV,bestTD,best_vionum,best_viocus]=decode(dpszx.Chrom(minInd(1),:),cusnum,cap,demands,a,b,L,s,dist,chesu,bl);
    disp(['车辆使用数目：',num2str(bestNV),'，车辆行驶总距离：',num2str(bestTD)]);
    fprintf('\\n')
    %% 更新迭代次数
    gen=gen+1 ;
end
%% 画出最优解的路线图
ObjV=calObj(dpszx.Chrom,cusnum,cap,demands,a,b,L,s,dist,alpha,belta,belta2,chesu,bl,ps);             %计算种群目标函数值
[minObjV,minInd]=min(ObjV);
%% 输出最优解的路线和总距离
disp('最优解:')
bestChrom=dpszx.Chrom(minInd(1),:);
bestps=ps(minInd(1),:);
[bestVC,bestNV,bestTD,best_vionum,best_viocus]=decode(bestChrom,cusnum,cap,demands,a,b,L,s,dist,chesu,bl);
disp(['车辆使用数目：',num2str(bestNV),'，车辆行驶总距离：',num2str(bestTD)]);
disp('-------------------------------------------------------------')
% [cost]=costFuction(bestVC,a,b,s,L,dist,demands,cap,alpha,belta,belta2,chesu,bl,);
%% 画出最终路线图
draw_Best(bestVC,zuobiao,bestps);
% save c101.mat
% toc

结果


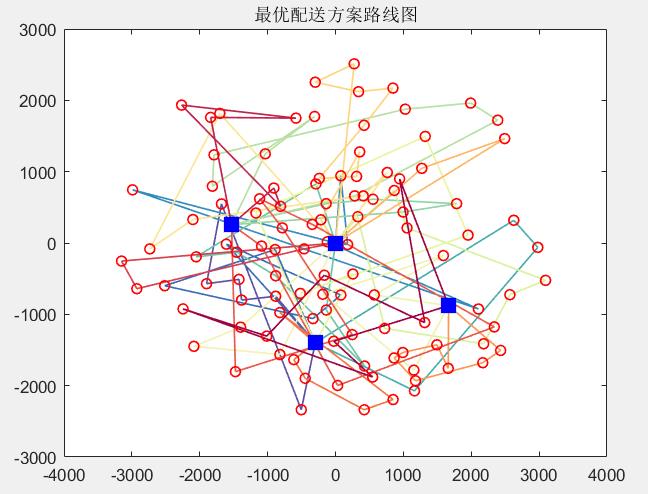
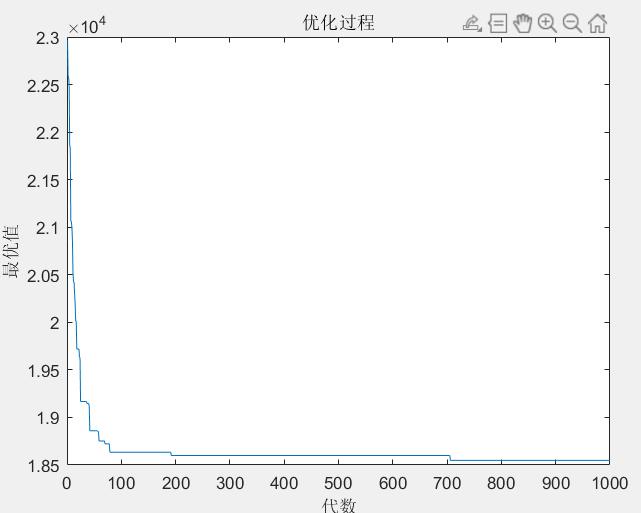
最优解:
车辆使用数目：20，车辆行驶总距离：186.7797

配送路线1：2->62->61->60->59->56->54->2
配送路线2：2->39->83->7->5->40->2
配送路线3：1->3->2->1->108->19->12->1
配送路线4：2->80->79->42->2
配送路线5：1->94->58->57->63->73->71->1
配送路线6：4->105->104->103->102->4
配送路线7：4->38->31->30->29->87->86->89->88->4
配送路线8：1->106->70->69->68->67->65->91->1
配送路线9：2->16->15->14->13->98->2
配送路线10：3->53->6->66->78->3
配送路线11：1->77->76->75->1
配送路线12：1->92->90->85->84->82->1
配送路线13：1->95->93->101->100->34->28->27->26->25->1
配送路线14：1->33->32->1
配送路线15：3->23->22->21->20->45->44->43->3
配送路线16：2->52->51->50->49->48->2
配送路线17：4->74->72->97->24->4->18->46->96->4
配送路线18：1->107->11->10->1
配送路线19：4->99->41->35->37->36->4
配送路线20：3->47->55->9->8->64->17->81->3

如需帮助：
VX：zzs1056600403