基于DNA序列的图像加解密算法仿真
Posted 51matlab
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了基于DNA序列的图像加解密算法仿真相关的知识,希望对你有一定的参考价值。
1.算法仿真效果
matlab2022a仿真结果如下:
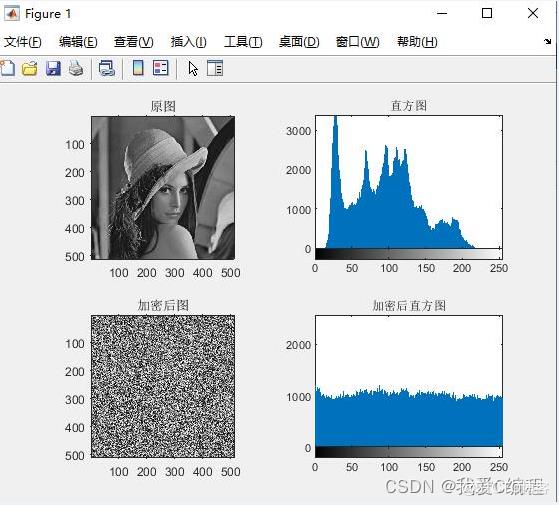
2.算法涉及理论知识概要
随着互联网和通信行业的快速发展,信息安全也越来越受关注,由此很多数据加密算法被提出,并被大量使用,例如AES算法,DES算法等,由于人在生活中所获得的信息大部分来自于视觉,图像就成为了人类生活活动中最常见的信息载体.高辨识率的图像越来越受人们的欢迎,使得数字图像具有数据量大,冗余度高,像素之间相关性强等特征,传统的数据加密算法不适用于数字图像加密[1-2],为防止图像信息泄露,人们提出了很多不同的加密算法文献[3-6],其目的是将有意义的原始图像转换为无法识别或类似噪声的密文图像,从而达到对原始图像进行保护的效果.例如,在图像加密算法中,人们提出了很多位级的图像加密算法.因为与像素级置乱相比,比特置乱的优点是可以同时改变像素位置和像素值,而且具有较好的加密效果.文献[4]的置换过程中利用广义Arnold映射生成的随机序列对彩色图像的三维位矩阵进行置乱,再用交叉方式对置乱后的三个平面分量进行扩散,性能分析表明加密方案是安全有效的.而近年来,基于DNA的图像加密方案越来越受研究者的关注,因为DNA技术具有并行性高、存储量大、功耗低的特点,同时还可以在DNA碱基之间进行操作.所以很多研究者将混沌系统和DNA编码结合.文献[5]采用了一种跨信道操作的图像加密方案,采用DNA减法和异或运算对普通图像的红、绿、蓝信道进行交叉操作,提高普通图像的随机性.在文献[6]中,作者对产生的混沌序列进行8等分,来产生DNA编码规则,但是这样产生的编码序列存在缺点.因为混沌序列分布不均匀的问题会导致选取DNA编码规则的次数相差较大的现象,使得攻击者可以通过统计分析很容易获得一些与原始图像相关并且有用的信息.
为了解决数字图像加密算法复杂度高、安全性较差的问题,提出一种基于混沌系统的DNA融合图像加密算法。首先利用Baker变换对图像进行置乱以读取DNA序列;再由Logistic混沌映射产生混沌序列,从而对DNA序列进行混沌加密。该算法对初值具有很好的敏感性,抗统计、抗差分攻击能力强。
一个链DNA,由四个不同的基本核苷酸组成:腺嘌呤( A)、胸腺嘧啶(T)、胞嘧啶(C)和鸟嘌呤(G),这4种核苷酸能够结合在一起形成一条长序列,且A与T配对,C与G配对。通过规定A、C、G、T分别编码为00,01,10,11,这样的编码方案有24种,但只有8种编码方案满足Watson-Crick规则,如表1。假设规定A-OO、T-O1、C-10、G-11,如二进制序列101 10100,DNA序列可以写成GTCA。
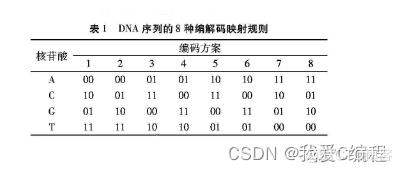
随着DNA计算的飞速发展,一些研究人员提出基于DNA序列的某些生物学操作和代数运算,如加法运算。DNA序列加法和减法运算是源于在传统二进制中加法和减法。
对应于8种DNA编码方案,也存在8种DNA加法运算和8种DNA减法运算。如表2—3所示,从中可看出任何一个基因在每行或列中是唯一的,即加法运算和减法运算的结果有且只有一个。
3.MATLAB核心程序
if co_dec==0
t = length(img);
a1 = bitand(img,192)/64;
a2 = bitand(img,48)/16;
a3 = bitand(img,12)/4;
a4 = bitand(img,3);
A =[a1,a2,a3,a4];
%rule_pointer
if rule==1
for i=1:t
for j=1:4*t
if A(i,j)==0
dna_code(i,j)=\'A\';
elseif A(i,j)==1
dna_code(i,j)=\'C\';
elseif A(i,j)==2
dna_code(i,j)=\'G\';
else
dna_code(i,j)=\'T\';
end
end
end
end
if rule==2
for i=1:t
for j=1:4*t
if A(i,j)==0
dna_code(i,j)=\'A\';
elseif A(i,j)==1
dna_code(i,j)=\'G\';
elseif A(i,j)==2
dna_code(i,j)=\'C\';
else
dna_code(i,j)=\'T\';
end
end
end
end
if rule==3
for i=1:t
for j=1:4*t
if A(i,j)==0
dna_code(i,j)=\'T\';
elseif A(i,j)==1
dna_code(i,j)=\'C\';
elseif A(i,j)==2
dna_code(i,j)=\'G\';
else
dna_code(i,j)=\'A\';
end
end
end
end
if rule==4
for i=1:t
for j=1:4*t
if A(i,j)==0
dna_code(i,j)=\'T\';
elseif A(i,j)==1
dna_code(i,j)=\'G\';
elseif A(i,j)==2
dna_code(i,j)=\'C\';
else
dna_code(i,j)=\'A\';
end
end
end
end
if rule==5
for i=1:t
for j=1:4*t
if A(i,j)==0
dna_code(i,j)=\'G\';
elseif A(i,j)==1
dna_code(i,j)=\'A\';
elseif A(i,j)==2
dna_code(i,j)=\'T\';
else
dna_code(i,j)=\'C\';
end
end
end
end
if rule==6
for i=1:t
for j=1:4*t
if A(i,j)==0
dna_code(i,j)=\'G\';
elseif A(i,j)==1
dna_code(i,j)=\'T\';
elseif A(i,j)==2
dna_code(i,j)=\'A\';
else
dna_code(i,j)=\'C\';
end
end
end
end
if rule==7
for i=1:t
for j=1:4*t
if A(i,j)==0
dna_code(i,j)=\'C\';
elseif A(i,j)==1
dna_code(i,j)=\'A\';
elseif A(i,j)==2
dna_code(i,j)=\'T\';
else
dna_code(i,j)=\'G\';
end
end
end
end
if rule==8
for i=1:t
for j=1:4*t
if A(i,j)==0
dna_code(i,j)=\'C\';
elseif A(i,j)==1
dna_code(i,j)=\'T\';
elseif A(i,j)==2
dna_code(i,j)=\'A\';
else
dna_code(i,j)=\'G\';
end
end
end
end
else
[m,n]=size(img);
if rule==1
for i=1:m
for j=1:n
if img(i,j)==\'A\'
A(i,j)=0;
elseif img(i,j)==\'T\'
A(i,j)=3;
elseif img(i,j)==\'G\'
A(i,j)=2;
else
A(i,j)=1;
end
end
end
end
if rule==2
for i=1:m
for j=1:n
if img(i,j)==\'A\'
A(i,j)=0;
elseif img(i,j)==\'T\'
A(i,j)=3;
elseif img(i,j)==\'G\'
A(i,j)=1;
else
A(i,j)=2;
end
end
end
end
if rule==3
for i=1:m
for j=1:n
if img(i,j)==\'A\'
A(i,j)=3;
elseif img(i,j)==\'T\'
A(i,j)=0;
elseif img(i,j)==\'G\'
A(i,j)=2;
else
A(i,j)=1;
end
end
end
end
if rule==4
for i=1:m
for j=1:n
if img(i,j)==\'A\'
A(i,j)=3;
elseif img(i,j)==\'T\'
A(i,j)=0;
elseif img(i,j)==\'G\'
A(i,j)=1;
else
A(i,j)=2;
end
end
end
end
if rule==5
for i=1:m
for j=1:n
if img(i,j)==\'A\'
A(i,j)=1;
elseif img(i,j)==\'T\'
A(i,j)=2;
elseif img(i,j)==\'G\'
A(i,j)=0;
else
A(i,j)=3;
end
end
end
end
if rule==6
for i=1:m
for j=1:n
if img(i,j)==\'A\'
A(i,j)=2;
elseif img(i,j)==\'T\'
A(i,j)=1;
elseif img(i,j)==\'G\'
A(i,j)=0;
else
A(i,j)=3;
end
end
end
end
if rule==7
for i=1:m
for j=1:n
if img(i,j)==\'A\'
A(i,j)=1;
elseif img(i,j)==\'T\'
A(i,j)=2;
elseif img(i,j)==\'G\'
A(i,j)=3;
else
A(i,j)=0;
end
end
end
end
if rule==8
for i=1:m
for j=1:n
if img(i,j)==\'A\'
A(i,j)=2;
elseif img(i,j)==\'T\'
A(i,j)=1;
elseif img(i,j)==\'G\'
A(i,j)=3;
else
A(i,j)=0;
end
end
end
end
A1=A(:,1:m);
A2=A(:,m+1:2*m);
A3=A(:,2*m+1:3*m);
A4=A(:,3*m+1:4*m);
dna_code=A1*64+A2*16+A3*4+A4;
end
MATLAB教程案例29基于Baker映射和Logistic混沌序列的图像加解密matlab实现
目录
以上是关于基于DNA序列的图像加解密算法仿真的主要内容,如果未能解决你的问题,请参考以下文章
图像加密基于matlab混沌系统和DNA编码彩色图像加密解密抗噪声性能分析含Matlab源码 2414期
MATLAB教程案例29基于Baker映射和Logistic混沌序列的图像加解密matlab实现
m基于POCS算法的空域序列图像超分辨率重建matlab仿真