图像加密基于matlab混沌系统和DNA编码彩色图像加密解密抗噪声性能分析含Matlab源码 2414期

Posted 2023-03-10 海神之光

⛄一、DNA混沌系统图像加密简介

0 引 言
数字图像作为信息传播的重要载体,广泛应用于教育、军事和医疗等领域。其在传播过程中可能会受到人为攻击,故对于数字图像的安全性研究成为人们关注的焦点,而通过图像加密技术能够确保图像进行安全的传输和存储[1]。混沌系统具有不可预测性、伪随机性且对初始条件极敏感,据此产生了许多基于混沌的数字图像加密算法[2,3,4]。文献[2]提出一种基于图像分割和多扩散模型的混沌加密方法,具有很好的安全特性。文献[3]提出的混沌图像加密算法中,将分块置乱与动态索引扩散相结合,特点是快速且安全。文献[4]提出了基于分数阶统一混沌系统的图像加密算法,在保持高安全性的同时拥有较低的时间复杂度。

基因(DNA)计算具有低功耗、大存储量、高信息密度等优点,为数字图像加密开拓了新的研究方向。文献[5]提出了一种基于DNA编码的混沌图像加密算法,但其采用单一的DNA编码规则。而文献[6]早已指出采用固定的DNA编码方式很难抵抗选择明文攻击。文献[7]提出的算法虽然使用动态DNA编码方案解决这一问题,但其加密过程与明文无关,算法易受到已知明文和选择明文攻击[8]。

本文采用DNA随机编码方法,并结合混沌系统和SHA—384,提出一种彩色图像加密方法,以生成具有较好抗攻击能力的密文。

1 基本理论
1.1 Logistic映射
Logistic方程又称为虫口模型[9],其方程如下

x(n+1)=μx(n)[1-x(n)] (1)

式中 μ为系统参量,且 xn∈(0,1),μ∈(0,4],当μ∈(3.569 945 6,4]时,Logistic系统处于混沌态,具有非常复杂的动力学行为。

1.2 Lorenz系统
Lorenz系统[10]是由美国气象学家Lorenz提出。该系统的数学模型如下所示

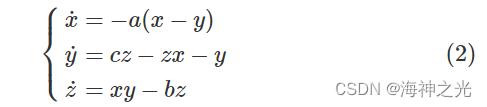
式中 x,y,z分别为系统变量;a,b,c分别为系统的参数。当a=10,b=8/3,c=28时,系统会进入混沌状态。

1.3 Hash函数
Hash函数是用于提供数据完整性和身份验证的加密原语,通过执行复杂操作来维持高级别的安全性,被广泛应用于实现数字签名算法等领域。在Hash算法中,与SHA—0和SHA—1相比,SHA—2更安全所以也更重要。SHA—2系列包含了很多散列函数,SHA—384是其中的一种散列函数。

本文通过明文图像灰度值和SHA—384产生一个384位的密钥,将其按每8位分段,其可表示为

K=k1,k2,k3,…,k48 (3)

Lorenz混沌映射的初始值计算如下

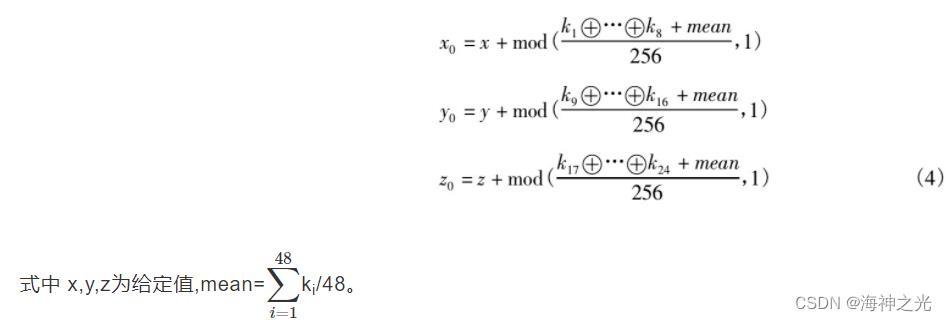
1.4 DNA编码与运算
DNA序列中碱基有4种: A(Adenine),C(Cytosine),G(Guanine)以及T(Thymine),其中A和T互补、C和G互补。类似的,二进制数00和11互补,01和10互补。如果用00,01,10和11分别代替A,C,G,T,则有24种编码规则,但是只有8种满足互补规则,如表1所示。

表1 DNA编码规则

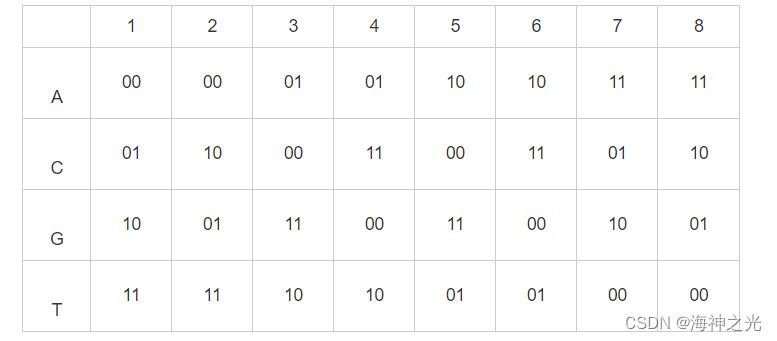
在图像密码系统中,像素的灰度值可以被表示8位二进制,然后编码成DNA序列。如果某个像素点的像素值为115,其二进制表示为‘01110011’,根据编码规则1,则可以得到‘CTAT’。

DNA序列的加、减和异或操作都基于二进制中的传统操作来定义,表2提供了在DNA编码规则5下的运算情况。
表2 DNA加/减/异或运算

2 加密方案
将明文图像分解成R,G,B三通道,以R通道为例对加密过程进行说明。

2.1 密码流的产生及DNA随机编码
假设明文图像R的大小为M×N,使用Logistic混沌系统得到一个长度为M×4N的混沌序列S(i),并对其进行量化处理,使其取值为1～8

S(i)=mod[(floor(S(i)×1014),8]+1 (5)

对于明文图像每个像素点的灰度值,都将其转换为二进制表示,结果将明文转换成大小为M×8N的二进制矩阵。将其展开为长度为M×8N的一维矩阵,每两个比特位为一组,这样与混沌序列S(i)中的值一一对应。对每两个比特位进行DNA编码,每次编码规则的选取都由对应位置的S(i)的取值决定,比如二进制矩阵的前两个数字为10,S(1)=5,则根据表1,10被编码为A。将一维矩阵全部数值编码完成后,将其重构成大小为M×4N的DNA矩阵H。

2.2 DNA平面置乱
1)借助于Lorenz混沌系统产生长度为M的随机向量 ,对其进行量化处理

X(i)=mod[(floor(X(i)×1013),M]+1 (6)

然后使DNA矩阵H的第i行与第i行进行位置互换,得到矩阵H′。

2)借助于Lorenz混沌系统产生长度为4N的随机向量Y(j),对其进行量化处理使其中每个随机数的取值在1-4N之间

Y(j)=mod[(floor(Y(j)×1013),4N]+1 (7)

然后使DNA矩阵H的第j行与第Y(j)列进行位置互换,得到矩阵H″。

3)通过混沌序列来获得交叉点,完成交叉置乱。交叉置乱旨在将进行交叉的两行(列)的部分组成进行置换。如GACTAATC与ACTTGAAC进行交叉操作,交叉点为2和5,那么两个DNA序列各自从第2个碱基到第5个碱基组成的序列完成位置互换,结果为GCTTGATC与AACTAAC。各交叉点可表示为

式中 at和bt分别为DNA矩阵中进行行交叉操作的第一个和第二个交叉点;cs和ds为进行列交叉操作的第一个和第二个交叉点。其中各个交叉点的具体值为

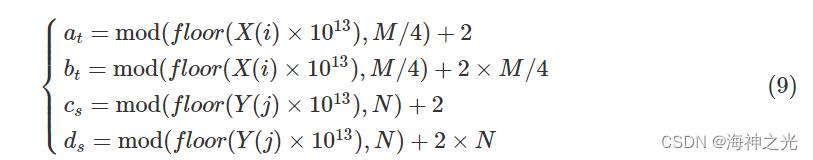
其中,t∈(1,M/2),s∈(0,2N)确定交叉点的位置后,H″的第i行与第M-i行,第j列与第4N-j列分别完成交叉置乱。得到矩阵I。

2.3 DNA平面扩散
将置乱后的DNA矩阵I分为大小都是M×2N的左半部分IH和右半部分IL,利用迭代结构进行扩散操作。在DNA迭代网络结构中,选取映射函数F1,F2为加密结构中的映射函数,两个加密密钥流K1=k1,k2,…,k2MN,K2=k1,k2,…,k2MN。输出的IH和IL分别影响下一个像素。DNA迭代网络加密具体过程如下:

1)利用Lorenz混沌系统,得到两个长度为2×M×N的混沌序列Z1和Z2,并对这两个序列作如下的处理

K1(i)=mod(floor(Z1(i)×1015),7) (10)

K2(i)=mod(floor(Z2(i)×1015),7) (11)

2)令i=1。

⛄二、部分源代码

%
%-------------------------------------------------------------------------------------------------------%
clear;clc;
I=imread(‘…/原始、加密、解密图片/lena.png’,‘png’); %读取图像信息
I1=I(:,:,1); %R
I2=I(:,:,2); %G
I3=I(:,:,3); %B
figure;imshow(I);title(‘原始图片’);
figure;imhist(I1);title(‘原始图片R通道直方图’);
figure;imhist(I2);title(‘原始图片G通道直方图’);
figure;imhist(I3);title(‘原始图片B通道直方图’);
% axis([0 255 0 4000]);
[M,N]=size(I1); %将图像的行列赋值给M,N
t=4; %分块大小

%% 原始图片R,G,B通道信息熵
%R通道
T1_R=imhist(I1); %统计图像R通道灰度值从0~255的分布情况，存至T1
S1_R=sum(T1_R); %计算整幅图像R通道的灰度值
xxs1_R=0; %原始图片R通道相关性
%G通道
T1_G=imhist(I2);
S1_G=sum(T1_G);
xxs1_G=0;
%B通道
T1_B=imhist(I3);
S1_B=sum(T1_B);
xxs1_B=0;

for i=1:256
pp1_R=T1_R(i)/S1_R; %每个灰度值占比，即每个灰度值的概率
pp1_G=T1_G(i)/S1_G;
pp1_B=T1_B(i)/S1_B;
if pp1_R~=0
xxs1_R=xxs1_R-pp1_Rlog2(pp1_R);
end
if pp1_G~=0
xxs1_G=xxs1_G-pp1_Glog2(pp1_G);
end
if pp1_B~=0
xxs1_B=xxs1_B-pp1_B*log2(pp1_B);
end
end

⛄三、运行结果

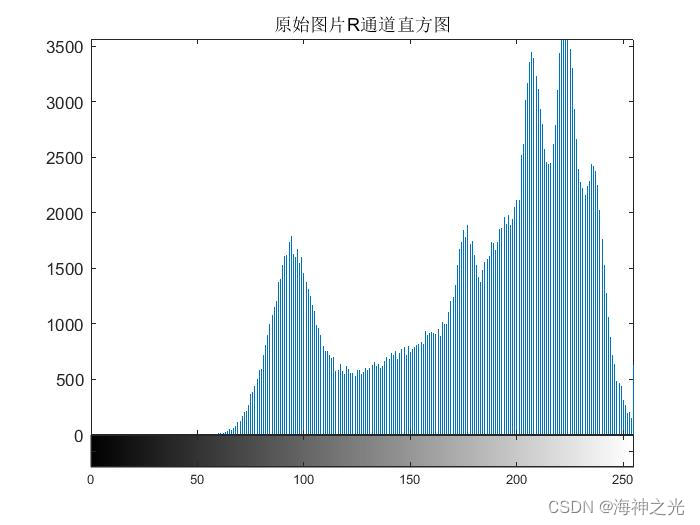
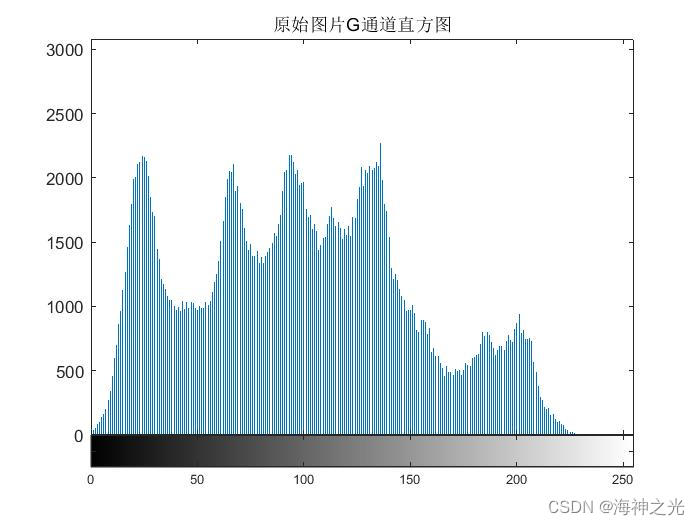
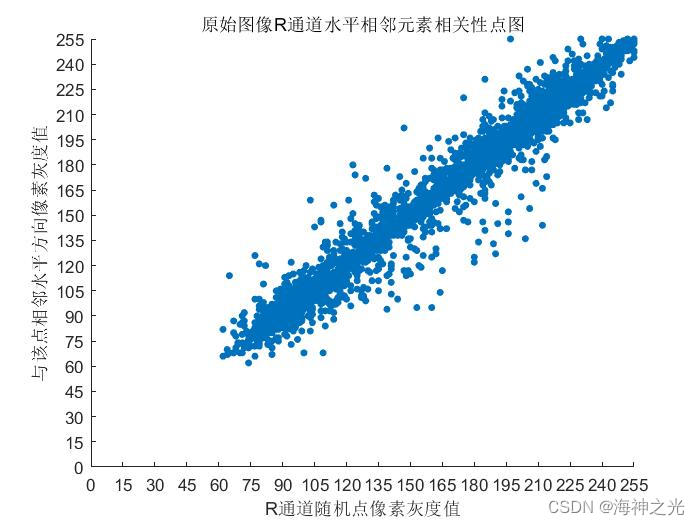
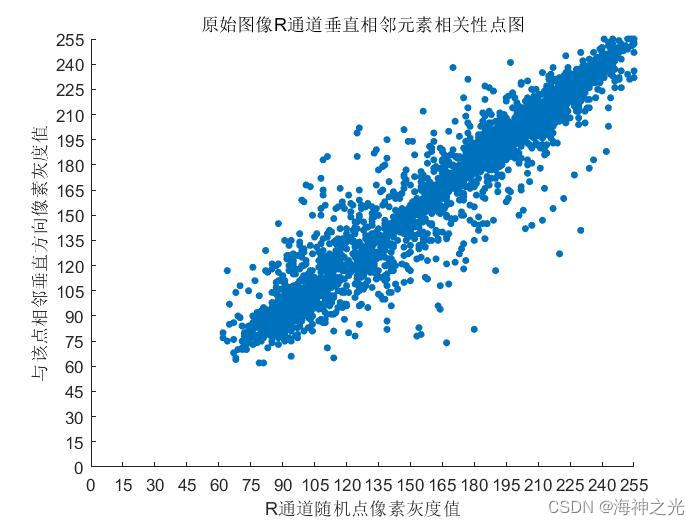
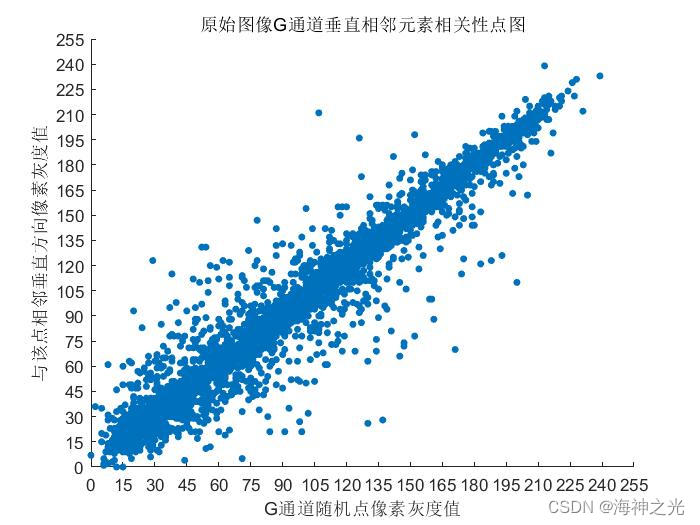
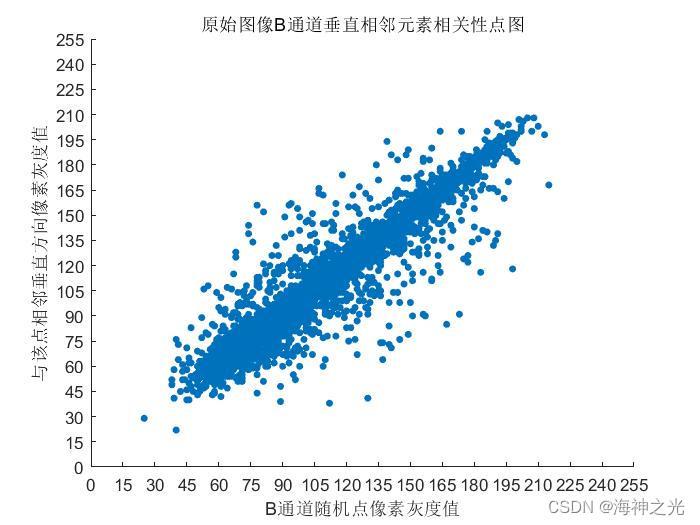
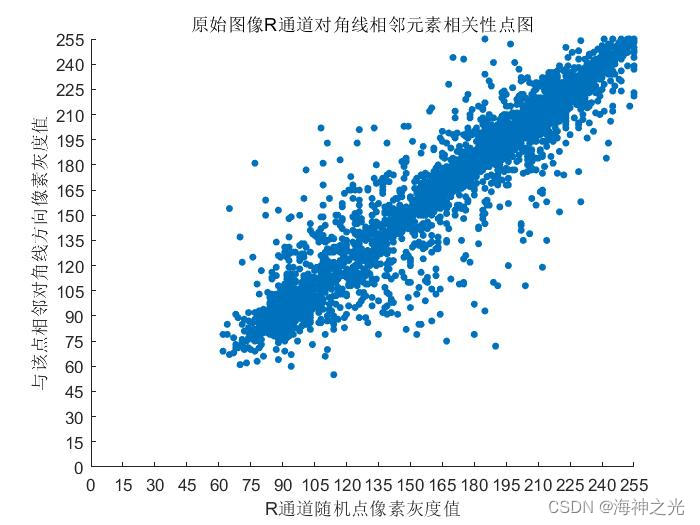
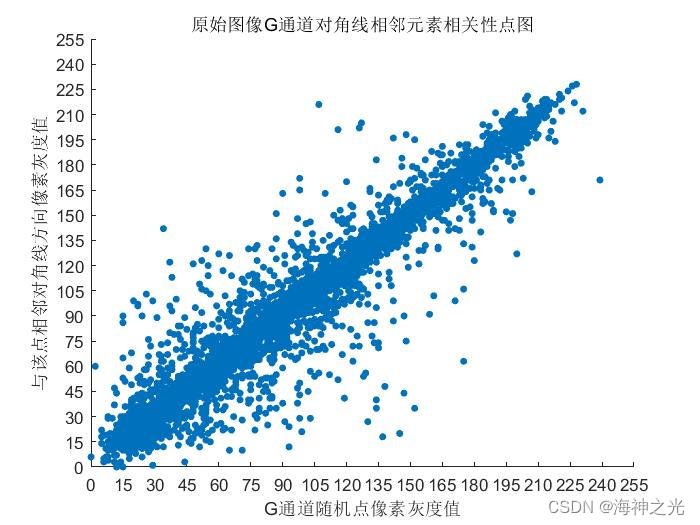
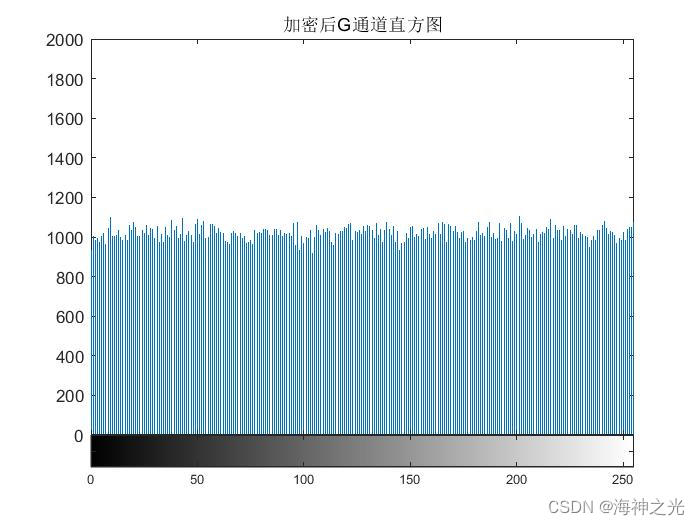
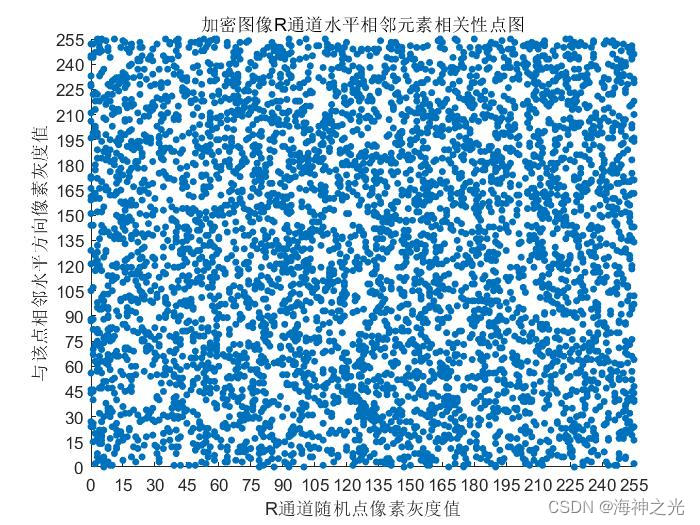
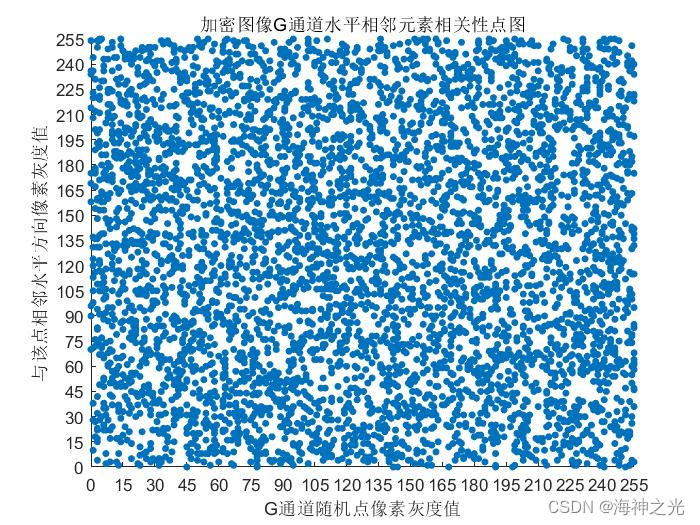
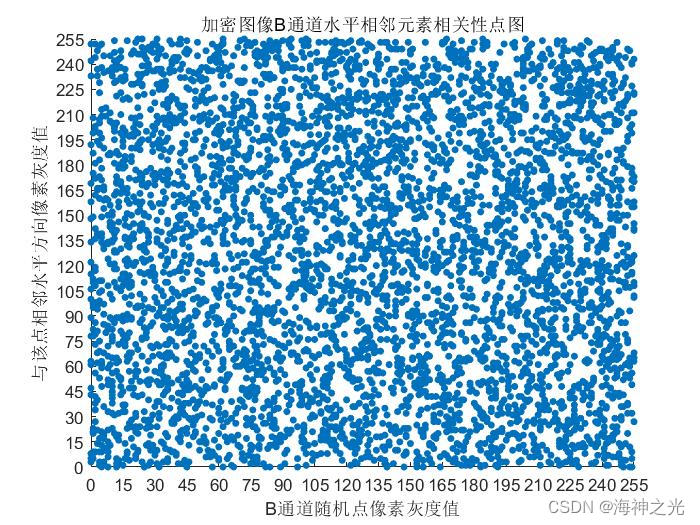
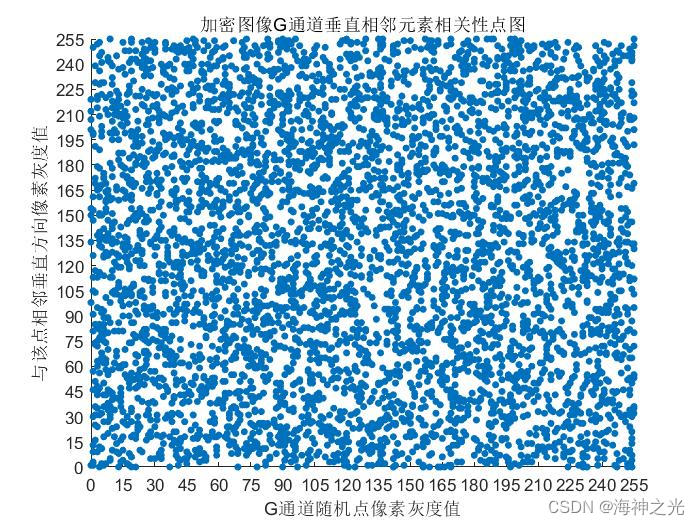
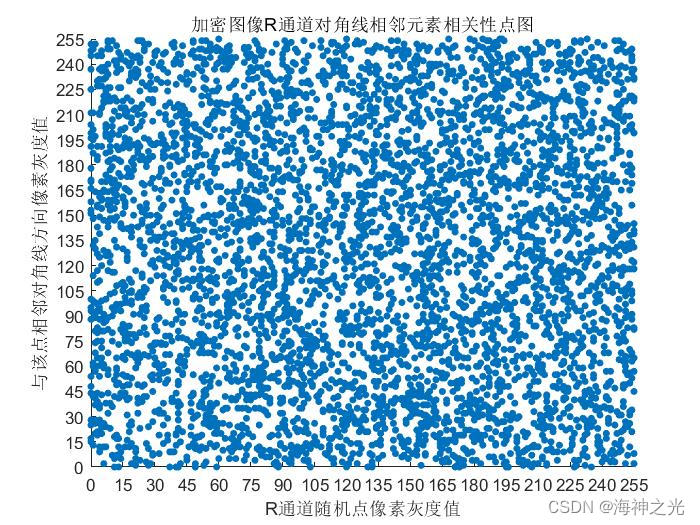
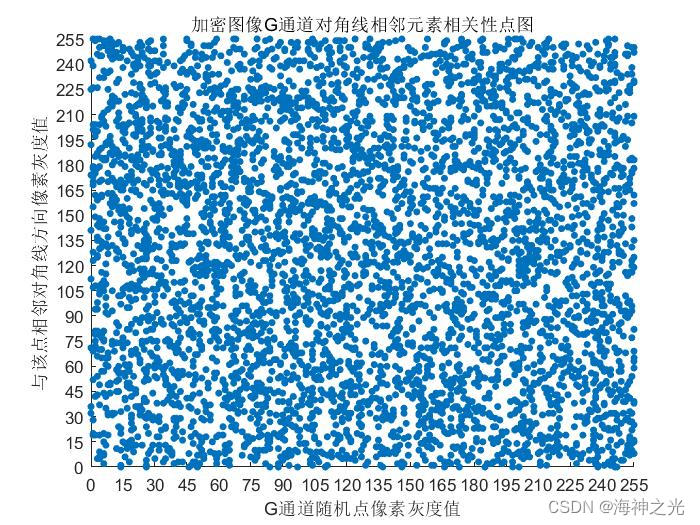
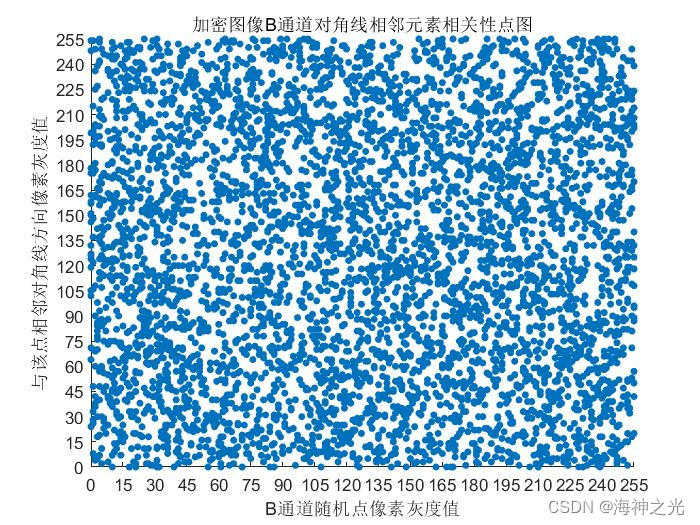
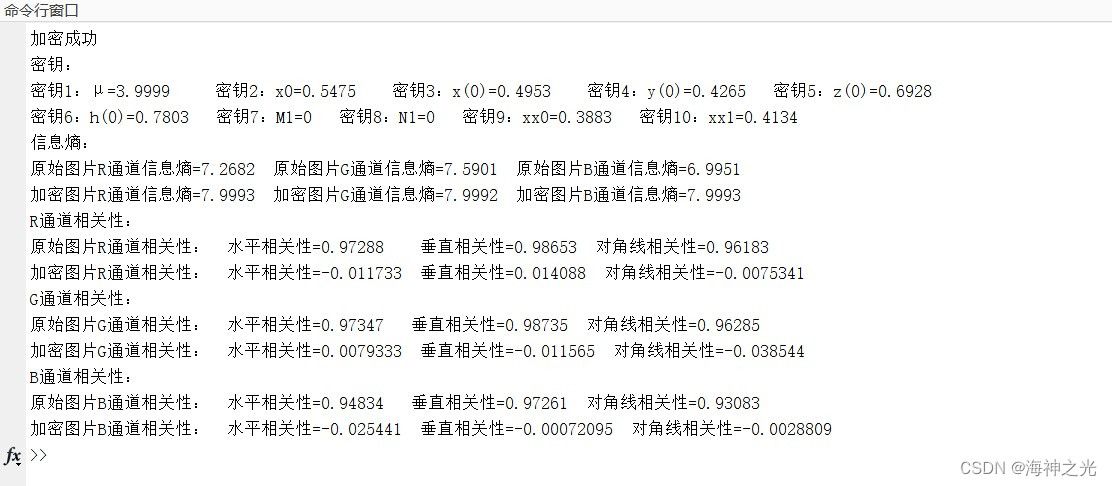
⛄四、matlab版本及参考文献

1 matlab版本
2014a

2 参考文献
[1]陈森,薛伟. 2021,42(10).基于混沌和DNA随机编码的彩色图像加密算法[J].传感器与微系统. 2021,40(08)

3 备注
简介此部分摘自互联网，仅供参考，若侵权，联系删除