python机器学习奇异值分解-SVD

Posted 2020-12-09 huanghanyu

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了python机器学习奇异值分解-SVD相关的知识，希望对你有一定的参考价值。

降维（Dimensionality Reduction）是机器学习中的一种重要的特征处理手段，它可以减少计算过程中考虑到的随机变量（即特征）的个数，其被广泛应用于各种机器学习问题中，用于消除噪声、对抗数据稀疏问题。它在尽可能维持原始数据的内在结构的前提下，得到一组描述原数据的，低维度的隐式特征（或称主要特征）。简单来说，在高维数据中筛选出对我们有用的变量，减小计算复杂度提高模型训练效率和准确率，这就是我们要说的降维。

MLlib机器学习库提供了两个常用的降维方法：奇异值分解（Singular Value Decomposition，SVD） 和 主成分分析（Principal Component Analysis，PCA），下面我们将通过实例介绍其具体的使用方法。

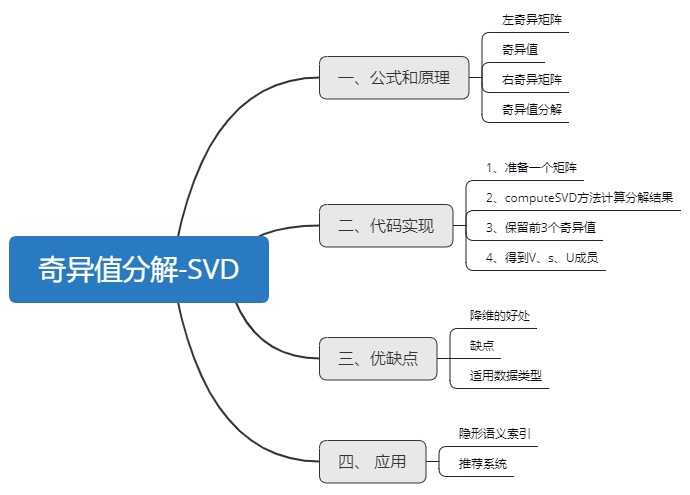
一、公式和原理

奇异值分解（SVD）将矩阵A分解为三个矩阵：U，Σ和V，如下公式

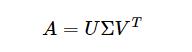
其中

左奇异矩阵 :，U 为一个标准正交矩阵，也叫实对称矩阵，怎么理解这个概念呢？就是说矩阵A的转置等于其本身，或者说矩阵U的维度为m×m ，用符号表示为

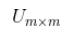
，我们称U 为左奇异矩阵。

奇异值 : Σ 是一个对角矩阵，仅在主对角线上有值，其它元素均为0，用符合表示为

，我们称Σ为奇异值。

右奇异矩阵 ： V也是一个正交矩阵，这会儿知道是啥意思了吧，和U的解释一样，用符号表示为

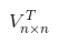
，我们称 V 为 右奇异矩阵。

奇异值分解 ：就是想要找到一个比较小的值k，保留前k个奇异向量和奇异值，其中 U 的维度从 m×m 变成了 m×k , V 的维度从 n×n 变成了 m×k ，Σ 的维度从 m×n 变成了 k×k 的方阵，从而达到降维效果。

二、代码实现

Mllib内置的奇异值分解功能位于org.apache.spark.mllib.linalg包下的RowMatrix和IndexedRowMatrix类中，所以，我们必须先通过已有数据创建出相应矩阵类型的对象，然后调用该类的成员方法来进行SVD分解，这里以RowMatrix为例：

import org.apache.spark.SparkConf;
import org.apache.spark.api.java.JavaRDD;
import org.apache.spark.api.java.JavaSparkContext;
import org.apache.spark.mllib.linalg.Matrix;
import org.apache.spark.mllib.linalg.SingularValueDecomposition;
import org.apache.spark.mllib.linalg.Vector;
import org.apache.spark.mllib.linalg.Vectors;
import org.apache.spark.mllib.linalg.distributed.RowMatrix;

3.1、准备一个矩阵

准备好一个矩阵，这里我们采用一个简单的文件a.mat来存储一个尺寸为(4,9)的矩阵，其内容如下：

1 2 3 4 5 6 7 8 9 
5 6 7 8 9 0 8 6 7 
9 0 8 7 1 4 3 2 1 
6 4 2 1 3 4 2 1 5

3.2、computeSVD方法计算分解结果

随后，将该文本文件读入成RDD[Vector]，并转换成RowMatrix，即可调用RowMatrix自带的computeSVD方法计算分解结果，这一结果保存在类型为SingularValueDecomposition的svd对象中

SparkConf conf = new SparkConf().setAppName("SVD").setMaster("local");
JavaSparkContext sc = new JavaSparkContext(conf);
        
JavaRDD<String> source = sc.textFile("data/mllib/a.data");
JavaRDD<Vector> data = source.map(line->{
    String[] parts = line.split(" ");
    return  Vectors.dense(Double.parseDouble(parts[0]),
            Double.parseDouble(parts[1]),
            Double.parseDouble(parts[2]));
});
RowMatrix rm = new RowMatrix(data.rdd());

3.3、保留前3个奇异值

SingularValueDecomposition<RowMatrix,Matrix> svd = rm.computeSVD(3,false,1.0E-9d);

3.4、得到V、s、U成员

通过访问svd对象的V、s、U成员分别拿到进行SVD分解后的右奇异矩阵、奇异值向量和左奇异矩阵：

System.out.println("s=================");
System.out.println(svd.s());
System.out.println("s=================");

System.out.println("V=================");
System.out.println(svd.V());
System.out.println("V=================");

System.out.println("U=================");
System.out.println(svd.U());
System.out.println("U=================");

控制台输出结果：

s========================================================
[28.741265581939565,10.847941223452608,7.089519467626695]
s========================================================

V===============================================================
-0.32908987300830383  0.6309429972945555    0.16077051991193514   
-0.2208243332000108   -0.1315794105679425   -0.2368641953308101   
-0.35540818799208057  0.39958899365222394   -0.147099615168733    
-0.37221718676772064  0.2541945113699779    -0.25918656625268804  
-0.3499773046239524   -0.24670052066546988  -0.34607608172732196  
-0.21080978995485605  0.036424486072344636  0.7867152486535043    
-0.38111806017302313  -0.1925222521055529   -0.09403561250768909  
-0.32751631238613577  -0.3056795887065441   0.09922623079118417   
-0.3982876638452927   -0.40941282445850646  0.26805622896042314 
V===============================================================
  
U====
null
U====

这里可以看到，由于限定了取前三个奇异值，所以奇异值向量s包含有三个从大到小排列的奇异值，而右奇异矩阵V中的每一列都代表了对应的右奇异向量。 U成员得到的是一个null值，这是因为在实际运用中，只需要V和S两个成员，即可通过矩阵计算达到降维的效果。

如果需要获得U成员，可以在进行SVD分解时，指定computeU参数，令其等于True，即可在分解后的svd对象中拿到U成员，如下文所示：

SingularValueDecomposition<RowMatrix,  Matrix> svd = rm.computeSVD(3,true,1.0E-9d);
System.out.println("U=================");
System.out.println(svd.U());
System.out.println("U=================");

控制台输出结果：

U============================================================
org.apache.spark.mllib.linalg.distributed.RowMatrix@25c2a9e3
U============================================================