AcWing 725. 完全数

Posted 2023-05-02 gao79138

AcWing 725. 完全数

---

1. 地址

    https://www.acwing.com/problem/content/description/727/

2. 题解

#include <iostream>
#include <cstdio>
#include <cmath>

using namespace std;

// 注意：这道题如果暴力解法一定TLE
// 因此，我们需要对其进行优化
int main()
    int n;
    scanf("%d",&n);
    while(n--)
        long number;
        scanf("%ld",&number);
        long sum = 0;
        //设i为第一个约数，那么number/i就为另外一个约数(最后一个)
        //因此我们只需要从i<=number/i的范围找约数即可
        //对上面的式子进行简化，可以得到i²<=number
        //进而i<=sqrt(number)
        for(int i=1;i<=sqrt(number);i++)
            //排除掉1,1的约数是1,题目要求排除本身
            if(number == 1)
                break;
            
            //i是约数
            if(number % i == 0)
                 sum += i;
                //排除掉因数是本身的情况
                if(number / i == number)
                    continue;
                else if(i == number / i)          //排除掉两个因数相等，从而重复计算的情况
                    continue;
                else
                    sum += number / i;
                
            
        
        if(number == sum)
            printf("%ld is perfect\\n",number);
        else
            printf("%ld is not perfect\\n",number);
        
    
    return 0;

2018-2019-2 20175310 个人项目报告2--完全数

2018-2019-2 20175310 个人项目报告2--完全数

定义：

如果一个数恰好等于它的因子之和，则称该数为“完全数”。第一个完全数是6，第二个完全数是28，第三个完全数是496，后面的完全数还有8128、33550336等等。

需求分析：

根据完全数的定义，用Java语言进行设计实现。

设计实现：

这里我实现的是列举出1000以内所有的完全数。
伪代码如下：

1、本项目有两个循环，外部的循环i表示遍历`1-1000`的所有数
2、内部的循环`j`是用于计算数`i`除本身以外其他因子的和`sum`
3、判断`sum`是否与`i`相等，若相等则输出完全数i，否则`i++`，计算下一个数

难点总结：

这个程序的难点主要在于计算因子，我一开始没想到用两个for循环嵌套的方法，准备在第一个for循环里调用一个用于计算因子的类，然后再算因子的和。不过这种方法过于繁琐，绕了弯路，其实只需在for循环里再加个for循环，用取余看结果是否为0，判断是不是因子。
核心代码如下：

for (int i = 1; i <= 1000; i++) {
            // 表示因子之和
            int sum = 0;
            for (int j = 1; j < i / 2 + 1; j++) {
                // 如果i能被j整除
                if (i % j == 0) {
                    //sum就加上i的因子j
                    sum += j;
                }
            }
            // 如果sum与i相等，说明是完全数。
            if (sum == i) {
                System.out.println(i);
            }
        }

运行结果截图：

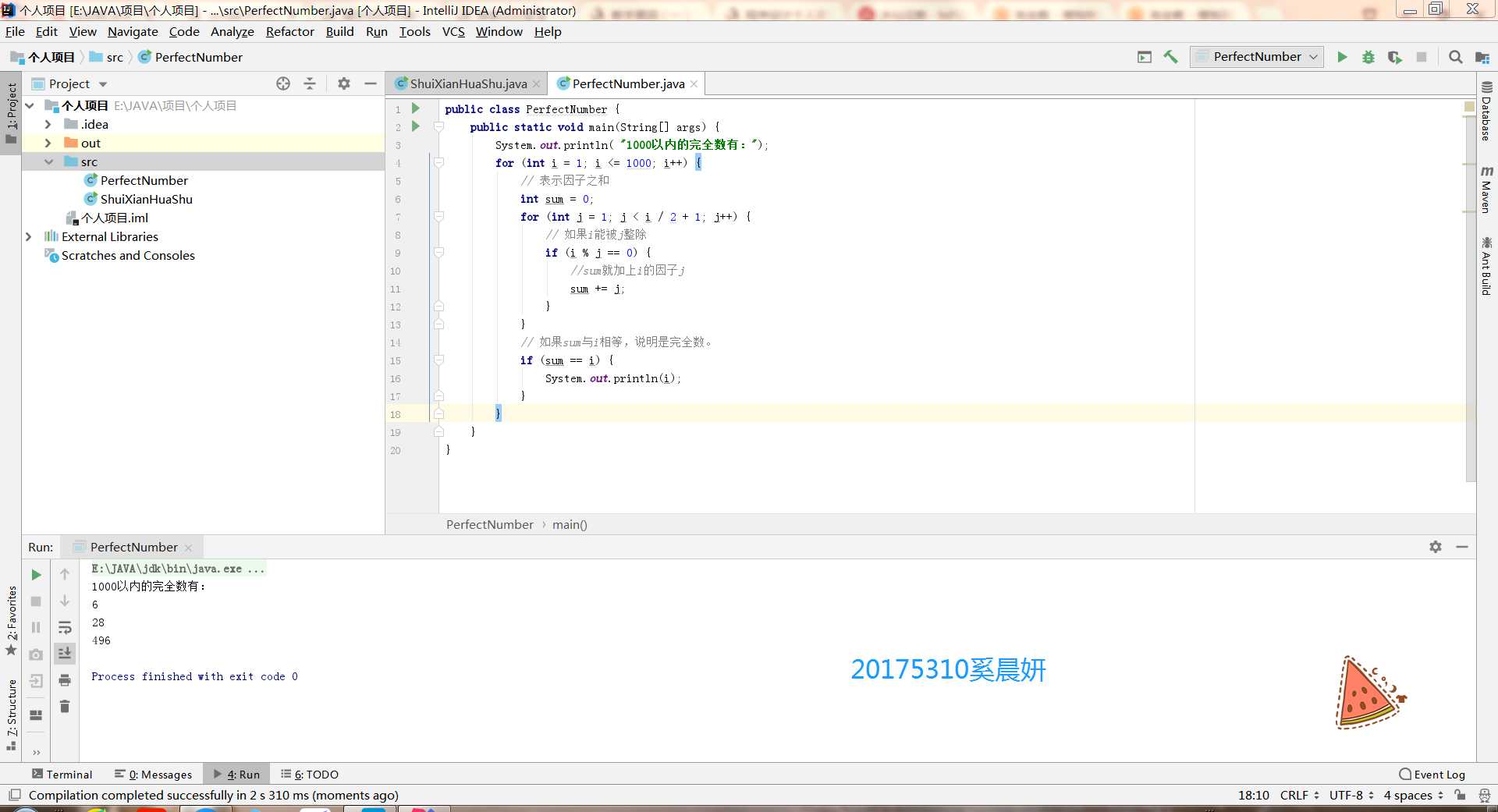
码云链接

PSP时间

步骤	耗时（min）	百分比
需求分析	10	11%
设计	20	22%
代码实现	30	33%
测试	10	11%
分析总结	20	22%