[ABC151E] Max-Min Sums

Posted 2023-05-02 OIerBoy

2023-03-11

题目

题目传送门

翻译

翻译

难度&重要性(1~10):5

题目来源

AtCoder

题目算法

数学

解题思路

对于一个正数 \\(x,x\\in A\\) 一定会有 \\(C_n^i\\) 次是作为集合中最大的元素，其中 \\(i\\) 表示比 \\(x\\) 小的数的个数，也一定会有 \\(C_n^j\\) 次是作为集合中最小的元素，其中 \\(j\\) 表示的是比 \\(x\\) 大的数的个数。
再从 \\(1\\) 到 \\(n\\) ，把其中每个数的作为最大的元素的次数与作为最小元素的次数统计出。

完成状态

已完成

51nod 1161 Partial Sums,1172 Partial Sums V2

这两题原理是一样的，不过第二题数据量大一些。这个累加操作相当于一个矩阵乘法，然后用矩阵中的第一列数和输入的数组做卷积，比如这个样例处理2次矩阵就是这样的

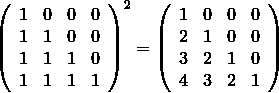
然后取出第一列数和输入的数做卷积，也就是多项式乘法

$\\left(1+2x+3x^2+4x^3\\right) \\left(1+3x+5x^2+6x^3\\right)=1 + 5 x + 14 x^2 + 29 x^3 + 39 x^4 + 38 x^5 + 24 x^6$

前四项的系数1，5，14，29就是结果了

这第一列数我们可以不用矩阵乘法做，经过观察发现它们是一些有关联的组合数，而且可以递推O(n)求出第一列数

$C_0=1,C_i=\\frac{C_{i-1} (i+k-1)}{i}$

 除法用逆元处理，第一题数据量小用O(n^2）模拟乘法就行了，Python写的

 1 n,k=map(int,raw_input().split())
 2 c=[1]*n
 3 p=10**9+7
 4 a=[int(input()) for i in xrange(n)]
 5 inv=[1]*5005
 6 for i in range(2,5005):
 7     inv[i] =(p-p//i) * inv[p%i] % p
 8 for i in xrange(1,n):
 9     c[i]=c[i-1]*(k-1+i)*inv[i]%p
10 c.reverse()
11 for i in xrange(1,n+1):
12     s=0
13     for j in xrange(i):
14         s=s+a[j]*c[-(i-j)]
15     print(s%p)

View Code

第二题50000数据就需要FFT了，还需要模1e9+7，我们用数论变换+中国剩余定理做

  1 #include <iostream>
  2 using namespace std;
  3 
  4 #define N 340030
  5 #define M 340020
  6 #define LL long long
  7 #define mod 1000000007
  8 #define K 3
  9 
 10 const int m[K] = {1004535809, 998244353, 104857601};
 11 const int G = 3;
 12 
 13 LL qpow(LL x, LL k, LL p) {
 14     int ret = 1;
 15     while(k) {
 16         if(k & 1) ret = 1LL * ret%p * x % p;
 17         k >>= 1;
 18         x = 1LL * x%p * x % p;
 19     }
 20     return ret;
 21 }
 22 struct _NTT {
 23     LL wn[25], p;
 24 
 25     void init(LL _p) {
 26         p = _p;
 27         for(int i = 1; i <= 21; ++i) {
 28             int t = 1 << i;
 29             wn[i] = qpow(G, (p - 1) / t, p);
 30         }
 31     }
 32     void change(LL *y, int len) {
 33         for(int i = 1, j = len / 2; i < len - 1; ++i) {
 34             if(i < j) swap(y[i], y[j]);
 35             int k = len / 2;
 36             while(j >= k) j -= k, k /= 2;
 37             j += k;
 38         }
 39     }
 40     void NTT(LL y[], int len, int on) {
 41         change(y, len);
 42         int id = 0;
 43         for(int h = 2; h <= len; h <<= 1) {
 44             ++id;
 45             for(int j = 0; j < len; j += h) {
 46                 LL w = 1;
 47                 for(int k = j; k < j + h / 2; ++k) {
 48                     int u = y[k];
 49                     int t = y[k+h/2] * w % p;
 50                     y[k] = u + t;
 51                     if(y[k] >= p) y[k] -= p;
 52                     y[k+h/2] = u + p - t;
 53                     if(y[k+h/2] >= p) y[k+h/2] -= p;
 54                     w = w * wn[id] % p;
 55                 }
 56             }
 57         }
 58         if(on == -1) {
 59             for(int i = 1; i < len / 2; ++i) swap(y[i], y[len-i]);
 60             int inv = qpow(len, p - 2, p);
 61             for(int i = 0; i < len; ++i)
 62                 y[i] = 1LL * y[i] * inv % p;
 63         }
 64     }
 65     void mul(LL A[], LL B[], LL len) {
 66         NTT(A, len, 1);
 67         NTT(B, len, 1);
 68         for(int i = 0; i < len; ++i) A[i] = 1LL * A[i] * B[i] % p;
 69         NTT(A, len, -1);
 70     }
 71 }ntt[K];
 72 
 73 LL tmp[N][K], t1[N], t2[N];
 74 LL x1[N], x2[N];
 75 LL r[K][K];
 76 
 77 LL CRT(LL a[]) {
 78     LL x[K];
 79     for(int i = 0; i < K; ++i) {
 80         x[i] = a[i];
 81         for(int j = 0; j < i; ++j) {
 82             int t = (x[i] - x[j]) % m[i];
 83             if(t < 0) t += m[i];
 84             x[i] = 1LL * t * r[j][i] % m[i];
 85         }
 86     }
 87     LL mul = 1, ret = x[0] % mod;
 88     for(int i = 1; i < K; ++i) {
 89         mul = 1LL * mul * m[i-1] % mod;
 90         ret += 1LL * x[i] * mul % mod;
 91         if(ret >= mod) ret -= mod;
 92     }
 93     return ret;
 94 }
 95 
 96 void mul(LL A[], LL B[], LL len) {
 97     for(int id = 0; id < K; ++id) {
 98         for(int i = 0; i < len; ++i) {
 99             t1[i] = A[i], t2[i] = B[i];
100         }
101         ntt[id].mul(t1, t2, len);
102         for(int i = 0; i < len; ++i) {
103             tmp[i][id] = t1[i];
104         }
105     }
106     for(int i = 0; i < len; ++i) A[i] = CRT(tmp[i]);
107 }
108 
109 LL a[N],b[N];
110 LL inv[50005];
111 
112 void init() {
113     for(int i = 0; i < K; ++i) {
114         for(int j = 0; j < i; ++j)
115             r[j][i] = qpow(m[j], m[i] - 2, m[i]);
116     }
117     for(int i = 0; i < K; ++i) ntt[i].init(m[i]);//ntt的初始化到这里结束
118     inv[1]=1;
119     for(int x=2;x<50003;x++)inv[x]=(mod-mod/x)*inv[mod%x]%mod;
120 }
121 
122 
123 int main()
124 {
125     init();
126     int n,k,i;
127     cin>>n>>k;
128     b[0]=1;
129     for(i=1;i<n;i++)
130     {
131         b[i]=b[i-1]*(k-1+i)%mod*inv[i]%mod;//求矩阵第一列系数
132         b[i]=(b[i]+mod)%mod;
133     }
134     for(i=0;i<n;i++)
135     {
136         cin>>a[i];
137     }
138     mul(a,b,1<<17);//做卷积
139     for(i=0;i<n;i++)
140     {
141         cout<<(a[i]+mod)%mod<<endl;
142     }
143     return 0;
144 }

View Code