[Python]CCF——碰撞的小球(201612-2)

Posted 2020-11-30 SavvyM

碰撞的小球

一、问题描述

问题描述
　　数轴上有一条长度为L（L为偶数)的线段，左端点在原点，右端点在坐标L处。有n个不计体积的小球在线段上，开始时所有的小球都处在偶数坐标上，速度方向向右，速度大小为1单位长度每秒。
　　当小球到达线段的端点（左端点或右端点）的时候，会立即向相反的方向移动，速度大小仍然为原来大小。
　　当两个小球撞到一起的时候，两个小球会分别向与自己原来移动的方向相反的方向，以原来的速度大小继续移动。
　　现在，告诉你线段的长度L，小球数量n，以及n个小球的初始位置，请你计算t秒之后，各个小球的位置。
提示
　　因为所有小球的初始位置都为偶数，而且线段的长度为偶数，可以证明，不会有三个小球同时相撞，小球到达线段端点以及小球之间的碰撞时刻均为整数。
　　同时也可以证明两个小球发生碰撞的位置一定是整数（但不一定是偶数）。
输入格式
输入的第一行包含三个整数n, L, t，用空格分隔，分别表示小球的个数、线段长度和你需要计算t秒之后小球的位置。
　　第二行包含n个整数a1, a2, …, an，用空格分隔，表示初始时刻n个小球的位置。
输出格式
　　输出一行包含n个整数，用空格分隔，第i个整数代表初始时刻位于ai的小球，在t秒之后的位置。
样例输入
3 10 5
4 6 8
样例输出
7 9 9
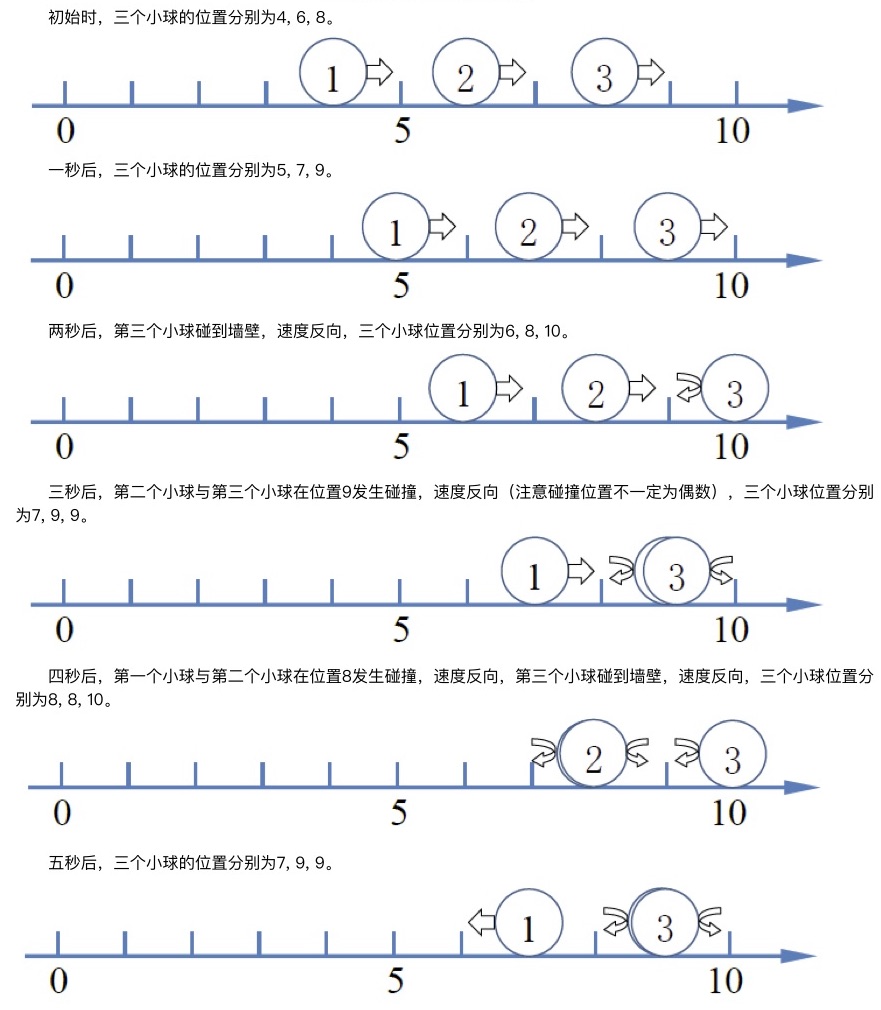
样例说明

样例输入
10 22 30
14 12 16 6 10 2 8 20 18 4
样例输出
6 6 8 2 4 0 4 12 10 2
评测用例规模与约定
　　对于所有评测用例，1 ≤ n ≤ 100，1 ≤ t ≤ 100，2 ≤ L ≤ 1000，0 < ai < L。L为偶数。
　　保证所有小球的初始位置互不相同且均为偶数。

# 碰撞的小球
def same(n,dic):
    count = 0
    for i in dic:
        if n == dic[i][0]:
            count += 1
    if count > 1:
        return True
    else:
        return False
n,L,t = map(int,input().split())
a = list(map(int,input().split()))
pos = {}
for i in range(n):
    pos[i+1] = [a[i],1]
for i in range(t):
    for j in pos:
        if pos[j][0] == 0:
            pos[j][1] = 1
        if pos[j][0] == L:
            pos[j][1] = -1
        if same(pos[j][0],pos):
            pos[j][1] *= -1
    for j in pos:
         pos[j][0] += pos[j][1]
for i in pos:
    print(pos[i][0],end=\' \')