基于python的递归简述

Posted 2020-11-28 icetree

前言：最近笔者敲代码练习练习就到了递归方面了，起初看各种文章讲解，都觉得大多数都说不到位，于是决定自己写一篇放在自己的博客空间。

1.递归的定义：直白点就是函数自己调用自己

2.递归运用的条件：临界值或者叫约束条件； 递归关系；

3.三个经典实例：

3.1 递归输出栈的格式

1 def digui(num):
2     print(num)
3     if num > 0:        
4         digui(num - 1)
5     else:
6         print("="*20)
7     print(num)
8 
9 digui(2)

输出结果入下图所示：

 

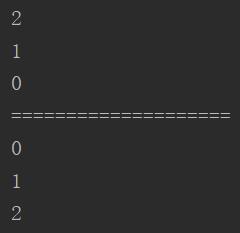
起初也是非常不解为啥会方向输出0 1 2，最后发现递归本身其实就是嵌入本身所有函数，这里看着可能会一头雾水，但是看到下面的代码就明白了：

在调用函数本身时，它之后的代码并没有结束，而是在等待条件为False 时，再接着执行之后的代码，同一个颜色的print()语句等待对应颜色的函数。

3.2 汉诺塔

汉诺塔规则：汉诺塔（Hanoi Tower），又称河内塔，源于印度一个古老传说。大梵天创造世界的时候做了三根金刚石柱子，在一根柱子上从下往上按照大小顺序摞着64片黄金圆盘。大梵天命令婆罗门把圆盘从下面开始按大小顺序重新摆放在另一根柱子上。并且规定，任何时候，在小圆盘上都不能放大圆盘，且在三根柱子之间一次只能移动一个圆盘。 为了不让电脑过于吃力此篇文章就用3或者4个圆盘为示例。

 

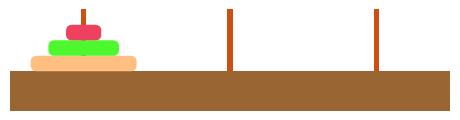也就是说：A，B，C三个圆柱，分别为初始位，过渡位，目标位，设A柱为初始位有n个圆盘，C位为最终目标位

（1）将最上面的n-1个圆盘从初始位移动到过渡位

（2）将初始位的最底下的一个圆盘移动到目标位

（3）将过渡位的n-1个圆盘移动到目标位

 1 # 汉诺塔编程
 2 i = 0
 3 def move(n,a,b,c):
 4     global i
 5     if n == 1:
 6         i +=1
 7         print(\'移动第\',i,\'次\',a,\'-->\',c)
 8     else:
 9         move(n-1,a,c,b)  # 本质是n-1个盘子从a到b
10         move(1,a,b,c)     # 本质是1个盘子从a到c
11         move(n-1,b,a,c)  #本质是n-1个盘子从b到c
12 
13 move(3,\'A\',\'B\',\'C\')

 

其中编程实现结果如下：

但是一般很难理解这个具体的递归程序，这里我把该递归进行了一个分解处理，但是提前声明：以后的递归运用不能像我这么来分解，一定要根据递归的运用条件也就是：递归关系、临界条件；分解处理如下所示：

 1 move(3,\'A\',\'B\',\'C):   
 2      move(2,A,C,B):
 3          move(1,A,B,C):
 4              print(A,\'-->\',C)
 5          move(1,A,C,B):
 6              print(A,\'-->\',B)
 7          move(1,C,A,B):
 8              print(C,\'-->\'B)     
 9      move(1,A,B,C):
10              print(A,\'-->\',C)   
11      move(2,B,A,C):
12          move(1,B,C,A):
13              print(B,\'-->\',A)
14          move(1,B,A,C):
15               print(B,\'-->\',C)
16          move(1,A,B,C):
17              print(A,\'-->\',C)

 看到上面的分解后应该会明白汉诺塔的工作流程了就是一直递推到2乃至到1进行基础的变换。

3.3斐波那契数列

 1 def fib(n):
 2     if n == 1:
 3         print([1])
 4     elif n == 2:
 5         print([1,1])
 6     else:
 7         fibs = [1, 1]
 8         for i in range(2, n):
 9             fibs.append(fibs[- 1] + fibs[- 2])
10         print(fibs)
11 
12 fib(10)

输出如下：

 

此处递归核心就是最后一个for循环，由于前面定义了数组中原有的2个数字，所以后面定义添加的长度是n-2，因为n-2+2=n，就是所要输出的长度，相应可以改变。该循环的核心意思是每一个新加的角标等于tuple的最后两位的相加。

 

4 参考资料

https://www.cnblogs.com/Fantinai/p/7806356.html