基于PSO粒子群优化的任务指派最优问题matlab仿真,并输出甘特图

Posted 2023-04-29 51matlab

1.算法仿真效果

matlab2022a仿真结果如下：

 

 

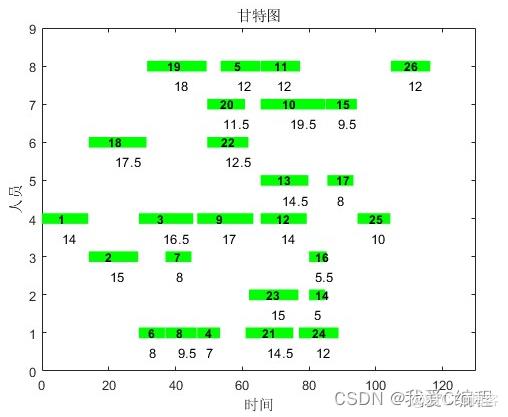
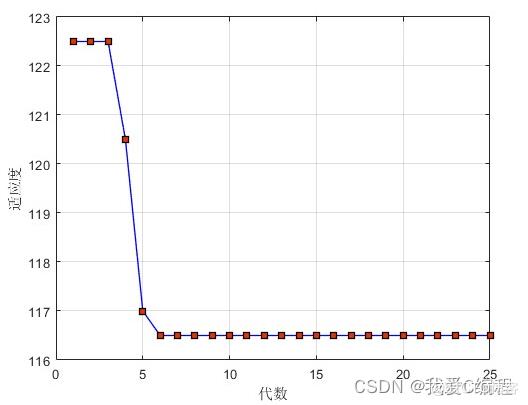
每个节点的人员:4  3  4  1  8  1  3  1  4  7  8  4  5  2  7  3  5  6  8  7  1  6  2  1  4  8

 

 

2.算法涉及理论知识概要

       PSO算法是一种随机的、并行的优化算法。它的优点是：不要求被优化函数具有可微、可导、连续等性质，收敛速度较快，算法简单，容易编程实现。然而，PSO算法的缺点在于：（1）对于有多个局部极值点的函数，容易陷入到局部极值点中，得不到正确的结果。造成这种现象的原因有两种，其一是由于待优化函数的性质；其二是由于微粒群算法中微粒的多样性迅速消失，造成早熟收敛。这两个因素通常密不可分地纠缠在一起。（2）由于缺乏精密搜索方法的配合，PSO算法往往不能得到精确的结果。造成这种问题的原因是PSO算法并没有很充分地利用计算过程中获得的信息，在每一步迭代中，仅仅利用了群体最优和个体最优的信息。（3）PSO算法虽然提供了全局搜索的可能，但是并不能保证收敛到全局最优点上。（4）PSO算法是一种启发式的仿生优化算法，当前还没有严格的理论基础，仅仅是通过对某种群体搜索现象的简化模拟而设计的，但并没有从原理上说明这种算法为什么有效，以及它适用的范围。因此，PSO算法一般适用于一类高维的、存在多个局部极值点而并不需要得到很高精度解的优化问题。

        当前针对PSO算法开展的研究工作种类繁多，经归纳整理分为如下八个大类：（1）对PSO算法进行理论分析，试图理解其工作机理；（2）改变PSO算法的结构，试图获得性能更好的算法；（3）研究各种参数配置对PSO算法的影响；（4）研究各种拓扑结构对PSO算法的影响；（5）研究离散版本的PSO算法；（6）研究PSO算法的并行算法；（7）利用PSO算法对多种情况下的优化问题进行求解；（8）将PSO算法应用到各个不同的工程领域。以下从这八大类别着手，对PSO算法的研究现状作一梳理。由于文献太多，无法面面俱到，仅捡有代表性的加以综述。

 

       PSO初始化为一群随机粒子（随机解）。然后通过迭代找到最优解。在每一次迭代中，粒子通过跟踪两个“极值（pbest和gbest）”来更新自己。在找到这两个最优值后，粒子通过下面的公式来更新自己的速度和位置。

 

 

 

 

 对于公式（1）：

 

公式（1）中的第一部分称为记忆项，表示上次速度大小和方向的影响；

公式（1）中的第二部分称为自身认知项，是从当前点指向粒子自身最好点的一个矢量，表示粒子的动作来源于自己经验的部分；

公式（1）中的第三部分称为群体认知项，是一个从当前点指向种群最好点的矢量，反映了粒子间的协调合作和知识共享。粒子就是通过自己的经验和同伴中最好的经验来决定下一步的运动。

 

 

3.MATLAB核心程序

 

[popu,s] = size(swarminit);
[en,n]=size(man);
tracee = ones(1,gen); 
tracee(1) = 10000000; % 初始全局最佳适应度设为足够大 
for i = 1:s,
    bestfit(i) = 10000000; % 初始个体历史最佳适应度设为足够大 
end
bestpar = swarminit; % 个体历史最佳粒子初始化
for l=1:swarminitnum,
    fitlist(l)=[0];
end
dd1=clock;
%==开始世代循环===============================
for step=1:gen, 
    for q=1:swarminitnum,
        for pop=1:n,
            time1(pop)=da(time(pop)/man(swarminitq(pop),pop));
        end   
        fitlist(q)=uncode(MM,n,time1,swarminitq,en);      
    end% 计算当前粒子群每个粒子的适应度
    [minval,sub] = min(fitlist); % 求得这代粒子的适应度最小值及其下标 
    if(tracee(step) > minval),  
        tracee(step) = minval;
        bestparticle = swarminitsub;
    end
    if(step~= gen) ,
       tracee(step+1)=tracee(step);% 全局最佳适应度及最佳粒子调整 
    end
 
     T=0.95*T;
   for i = 1:s,
       tt=fitlist(i)-bestfit(i);       
       if  (bestfit(i) > fitlist(i))|(min(1,exp(-tt/T))>=rand(1,1)) ,   
            bestfit(i) = fitlist(i); 
            bestpari = swarminiti;
       end  

 

　　

 

三维装箱基于matlab粒子群算法求解三维装箱优化问题含Matlab源码 950期

一、简介

1 粒子群算法的概念
粒子群优化算法(PSO：Particle swarm optimization) 是一种进化计算技术（evolutionary computation）。源于对鸟群捕食的行为研究。粒子群优化算法的基本思想：是通过群体中个体之间的协作和信息共享来寻找最优解．
PSO的优势：在于简单容易实现并且没有许多参数的调节。目前已被广泛应用于函数优化、神经网络训练、模糊系统控制以及其他遗传算法的应用领域。

2 粒子群算法分析
2.1基本思想
粒子群算法通过设计一种无质量的粒子来模拟鸟群中的鸟，粒子仅具有两个属性：速度和位置，速度代表移动的快慢，位置代表移动的方向。每个粒子在搜索空间中单独的搜寻最优解，并将其记为当前个体极值，并将个体极值与整个粒子群里的其他粒子共享，找到最优的那个个体极值作为整个粒子群的当前全局最优解，粒子群中的所有粒子根据自己找到的当前个体极值和整个粒子群共享的当前全局最优解来调整自己的速度和位置。下面的动图很形象地展示了PSO算法的过程：

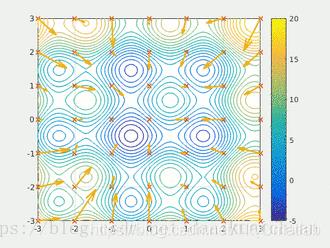
2 更新规则
PSO初始化为一群随机粒子(随机解)。然后通过迭代找到最优解。在每一次的迭代中，粒子通过跟踪两个“极值”(pbest，gbest)来更新自己。在找到这两个最优值后，粒子通过下面的公式来更新自己的速度和位置。