m基于simulink的负荷频率小波神经PID控制器仿真,并对比PID控制器
Posted 51matlab
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了m基于simulink的负荷频率小波神经PID控制器仿真,并对比PID控制器相关的知识,希望对你有一定的参考价值。
1.算法仿真效果
matlab2022a仿真结果如下:
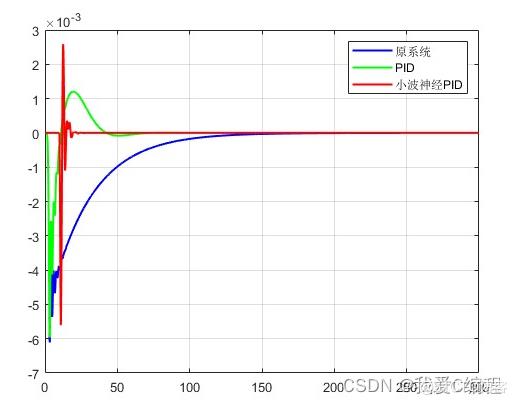
其对比仿真结果可知,原系统需要在150之后才开始收敛,PID是在50开始收敛,而采用WNN之后,系统用在经过短暂的抖动之后,迅速收敛。
2.算法涉及理论知识概要
随着电力工业的市场化改革、厂网分开,跨区域 电网的互联电力系统自动控制显得更加重要。电网 的频率稳定是电力系统安全稳定运行的重要因素, 是衡量电网稳定的重要指标。频率异常或频率崩 溃,将对电力系统本身及电力用户带来极为严重的 后果。频率与有功功率相关,电力系统中有功功率 的需求和产生上的任何变化都会反映到系统频率的 变化上。在跨区域电网的互联电力系统中,频率控 制更加复杂、导致的问题更严重。
频率是电力系统电能质量的三大指标之一,也是电气设备设计和制造的基本技术参数。电力系统频率超过允许的偏移值就会影响设备的安全运行,还可能造成供电设备和用电设备的损坏;频率质量的优劣直接影响电力系统的安全、稳定、经济、优质运行。电力系统频率是靠电力系统内并联运行的所有发电机机组发出的有功功率总和与系统内所有负荷消耗(包括网损)的有功功率总和之间的平衡来维持的,电力系统中有功功率的需求和产生上的任何变化都会反映到系统频率的变化上。在跨区域电网的互联电力系统中,频率控制更加复杂,导致的问题更严重。随着国民经济的不断发展和电力系统规模的不断增大,对频率质量的要求将越来越高。所谓负荷频率控制,是指通过控制系统内并联运行机组输入的总功率等于系统负荷在额定频率下所消耗的有功功率将电力系统频率控制在允许范围内的过程。
常规ANN采用Sigmoid函数作激发函数,这一 类全局基函数考虑的是输入信号的时域全局特点。 它的不足就在于对于广泛输入值的敏感性,结果网 络中所有的输入值和各个神经元的激发函数都将产 生相互影响,导致大量的参数调整和太长的计算学 习时间,收敛性差。
跨区域电网的互联电力系统LFC如果单纯由神 经网络等智能控制技术实现,则网络节点数将增大, 学习速度慢且不容易收敛。而区域内电网的小负荷 波动和脉动完全可以通过传统的PID控制调节平 衡。所以提出了结合WNN和传统PID的控制模型, 如图1所示。2个节点的WNN(图中虚框内)完成跨区域间的 平衡控制。a是小波函数的伸缩系数,b是平移系 数,p是输入到小波神经元的权值系数,q是小波神 经元的输出加到整个网络输出的权值系数,w是神 经元间的连接或反馈权值系数,T是小波元的时滞 常数,!是加到小波神经元的偏移参数。
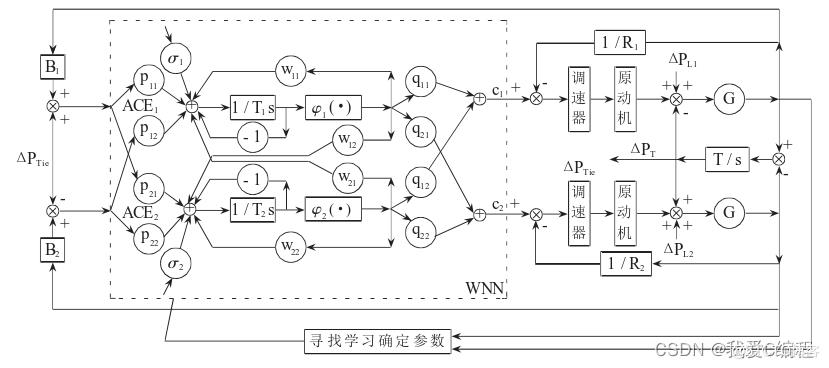
该LFC系统保留了传统的两级PID控制,PID 回路可以完成区域内的频率波动控制,从而减少神 经网络的节点数量。区域内的频率波动偏差信号经 PID回路控制调速器、原动机,从而控制发电机功率, 使区域内频率保持稳定。同时,区域内的频率波动 又会影响到互联的区域电网间。
3.MATLAB核心程序
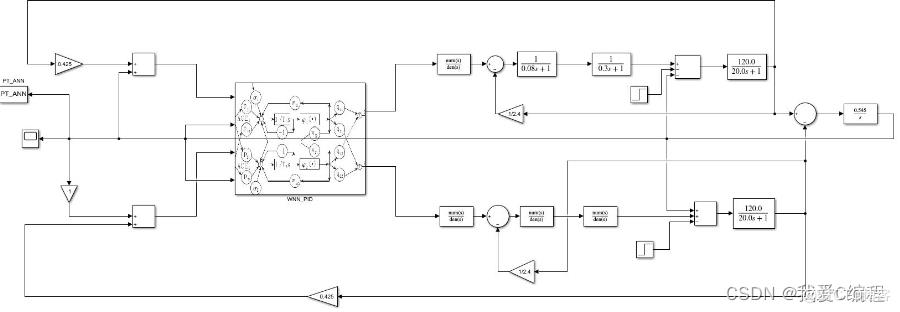

%后面的函数就是文件夹中的几个子函数,这里不做进一步的注释了。
%初始化函数
function [sys,x0,str,ts] = func_initialize()
sizes = simsizes; % 读入模板,得出默认的控制量
sizes.NumContStates = 0;
sizes.NumDiscStates = 3;
sizes.NumOutputs = 4+5*6;
sizes.NumInputs = 9+15*6;
sizes.DirFeedthrough = 1;
sizes.NumSampleTimes = 1;
sys = simsizes(sizes);
x0 = zeros(3,1);
str = [];
ts = [0.0005 0];
%离散状态变量更新函数
function sys = func_news(u)
sys=[u(1)-u(2);u(1);u(1)+u(3)-2*u(2)];
%输出量计算函数
function sys = func_wnn_out(t,x,u,K_pid,xite);
c3 = reshape(u(7 : 6+3*6) ,3,6);
c2 = reshape(u(7+5*6 : 6+8*6) ,3,6);
c1 = reshape(u(7+10*6: 6+13*6),3,6);
b3 = u(7+3*6 : 6+4*6);
b2 = u(7+8*6 : 6+9*6);
b1 = u(7+13*6: 6+14*6);
w3 = u(7+4*6 : 6+5*6);
w2 = u(7+9*6 : 6+10*6);
w1 = u(7+14*6: 6+15*6);
xx=u([6;4;5]);
if t==0
c1 = 30*ones(3,6);
b1 = 80*ones(6,1);
w1 = 2*ones(6,1);
K_pid0 = K_pid;
else
K_pid0=u(end-2:end);
end
%激发函数
for j=1: 6
h(j,1)=(1 - norm(xx-c1(:,j))^2/(b1(j)*b1(j))) * exp(-norm(xx-c1(:,j))^2/(2*b1(j)*b1(j)));
end
dym = u(4)-w1\'*h;
w = w1 + xite*dym*h + 0.05*(w1-w2) + 0.05*(w2-w3);
for j=1:6
d_bi(j,1)=xite*dym*w1(j)*h(j)*(b1(j)^(-3))*norm(xx-c1(:,j))^2;
d_ci(:,j)=xite*dym*w1(j)*h(j)*(xx-c1(:,j))*(b1(j)^(-2));
end
bi =b1 + d_bi + 0.05 * (b1-b2) + 0.05*(b2-b3);
ci =c1 + d_ci + 0.05 * (c1-c2) + 0.05*(c2-c3);
dJac=sum(w.*h.*(-xx(1)+ci(1,:)\')./bi.^2);
KK=K_pid0+u(1)*dJac*[0.1;0.1;0.1].*x;
sys=[u(6)+KK\'*x; KK; ci(:); bi(:); w(:)];
基于神经网络PID的负荷频率控制系统simulink实现
目录
作者ID :fpga和matlab
CSDN主页:https://blog.csdn.net/ccsss22?type=blog
擅长技术:
1.无线基带,无线图传,编解码
2.机器视觉,图像处理,三维重建
3.人工智能,深度学习
4.智能控制,智能优化
5.其他一、理论基础
人工神经网络(Artificial Neural Networks,简写为ANNs)也简称为神经网络(NNs)或称作连接模型(Connection Model),它是一种模仿动物神经网络行为特征,进行分布式并行信息处理的算法数学模型。这种网络依靠系统的复杂程度,通过调整内部大量节点之间相互连接的关系,从而达到处理信息的目的。
生物神经网络主要是指人脑的神经网络,它是人工神经网络的技术原型。人脑是人类思维的物质基础,思维的功能定位在大脑皮层,后者含有大约10^11个神经元,每个神经元又通过神经突触与大约103个其它神经元相连,形成一个高度复杂高度灵活的动态网络。作为一门学科,生物神经网络主要研究人脑神经网络的结构、功能及其工作机制,意在探索人脑思维和智能活动的规律。
人工神经网络是生物神经网络在某种简化意义下的技术复现,作为一门学科,它的主要任务是根据生物神经网络的原理和实际应用的需要建造实用的人工神经网络模型,设计相应的学习算法,模拟人脑的某种智能活动,然后在技术上实现出来用以解决实际问题。因此,生物神经网络主要研究智能的机理;人工神经网络主要研究智能机理的实现,两者相辅相成。
频率是电力系统电能质量的三大指标之一,也是电气设备设计和制造的基本技术参数。电力系统频率超过允许的偏移值就会影响设备的安全运行,还可能造成供电设备和用电设备的损坏;频率质量的优劣直接影响电力系统的安全、稳定、经济、优质运行。电力系统频率是靠电力系统内并联运行的所有发电机机组发出的有功功率总和与系统内所有负荷消耗(包括网损)的有功功率总和之间的平衡来维持的,电力系统中有功功率的需求和产生上的任何变化都会反映到系统频率的变化上。在跨区域电网的互联电力系统中,频率控制更加复杂,导致的问题更严重。随着国民经济的不断发展和电力系统规模的不断增大,对频率质量的要求将越来越高。
所谓负荷频率控制,是指通过控制系统内并联运行机组输入的总功率等于系统负荷在额定频率下所消耗的有功功率将电力系统频率控制在允许范围内的过程。
近年来, 很多新的控制技术应用于 LFC, 如智能 控制器、自适应控制器等。神经网络( ANN) 在电 力系统控制中取得了很好的应用效果。神经网络对于非线性函数具有良好的逼 近效果, 但往往又存在学习时间长、难以收敛、学习 中陷入局部最优解、对全局数据的敏感性以及神经 元数量随输入数据数量以指数级上升的维数灾难等 问题。 另一方面, 随着小波理论和多分辨率分析思想 的研究深入, 小波理论也在电力系统得到应用。 考虑到人工神经网络的非线性控制特点和不 足、小波函数表示非静态瞬变信号的特点, 本文提出 了一个新的基于小波和 ANN 技术, 并结合传统 PID 控制的 LFC 控制器模型, 应用于互联电力系统的负 荷频率控制。

设 c 为 WNN 的输出, cd 为期望的负荷频率控制 数据, 则 e( t) = c( t) - cd ( t) 为偏差函数, WNN 的代价 函数为:

为便于计算, 用有显式 数学表达式的 Mexican Hat 函数( 它实质是 Gaussian 函数的二次导数) 作为激发 函数:

一个小波神经元的输出为 :
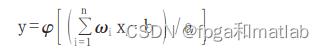
二、核心程序

function [sys,x0,str,ts]=func_wnn_pid(t,x,u,flag,K_pid,xite);
switch flag
case 0
[sys,x0,str,ts] = func_initialize();
case 2
sys = func_news(u);
case 3
sys = func_wnn_out(t,x,u,K_pid,xite);
case 1, 4, 9
sys = [];
end
%初始化函数
function [sys,x0,str,ts] = func_initialize()
sizes = simsizes; % 读入模板,得出默认的控制量
sizes.NumContStates = 0;
sizes.NumDiscStates = 3;
sizes.NumOutputs = 4+5*6;
sizes.NumInputs = 9+15*6;
sizes.DirFeedthrough = 1;
sizes.NumSampleTimes = 1;
sys = simsizes(sizes);
x0 = zeros(3,1);
str = [];
ts = [0.0005 0];
%离散状态变量更新函数
function sys = func_news(u)
sys=[u(1)-u(2);u(1);u(1)+u(3)-2*u(2)];
%输出量计算函数
function sys = func_wnn_out(t,x,u,K_pid,xite);
c3 = reshape(u(7 : 6+3*6) ,3,6);
c2 = reshape(u(7+5*6 : 6+8*6) ,3,6);
c1 = reshape(u(7+10*6: 6+13*6),3,6);
b3 = u(7+3*6 : 6+4*6);
b2 = u(7+8*6 : 6+9*6);
b1 = u(7+13*6: 6+14*6);
w3 = u(7+4*6 : 6+5*6);
w2 = u(7+9*6 : 6+10*6);
w1 = u(7+14*6: 6+15*6);
xx=u([6;4;5]);
if t==0
c1 = 30*ones(3,6);
b1 = 80*ones(6,1);
w1 = 2*ones(6,1);
K_pid0 = K_pid;
else
K_pid0=u(end-2:end);
end
%激发函数
for j=1: 6
h(j,1)=(1 - norm(xx-c1(:,j))^2/(b1(j)*b1(j))) * exp(-norm(xx-c1(:,j))^2/(2*b1(j)*b1(j)));
end
dym = u(4)-w1'*h;
w = w1 + xite*dym*h + 0.05*(w1-w2) + 0.05*(w2-w3);
for j=1:6
d_bi(j,1)=xite*dym*w1(j)*h(j)*(b1(j)^(-3))*norm(xx-c1(:,j))^2;
d_ci(:,j)=xite*dym*w1(j)*h(j)*(xx-c1(:,j))*(b1(j)^(-2));
end
bi =b1 + d_bi + 0.05 * (b1-b2) + 0.05*(b2-b3);
ci =c1 + d_ci + 0.05 * (c1-c2) + 0.05*(c2-c3);
dJac=sum(w.*h.*(-xx(1)+ci(1,:)')./bi.^2);
KK=K_pid0+u(1)*dJac*[0.1;0.1;0.1].*x;
sys=[u(6)+KK'*x; KK; ci(:); bi(:); w(:)];
三、仿真测试结果
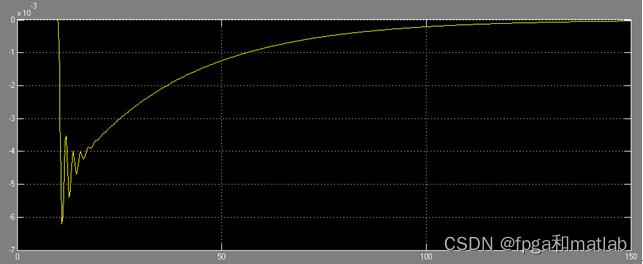
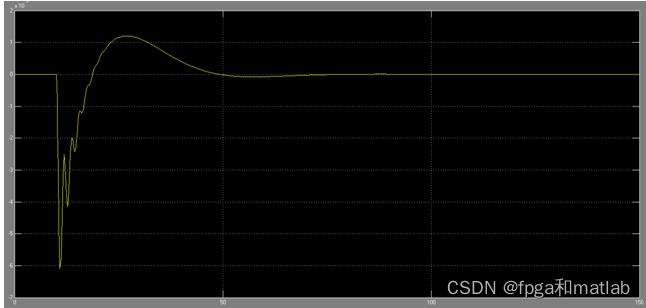
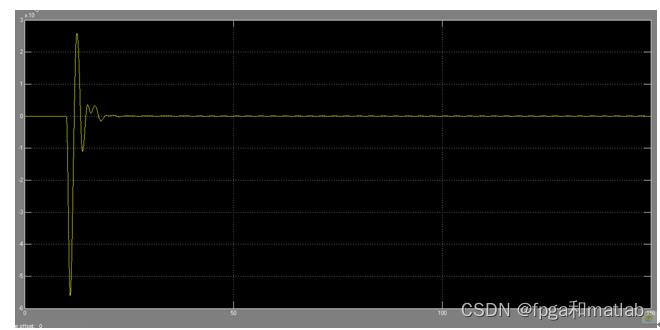

其对比仿真结果可知,原系统需要在150之后才开始收敛,PID是在50开始收敛,而采用WNN之后,系统用在经过短暂的抖动之后,迅速收敛。
A08-11
以上是关于m基于simulink的负荷频率小波神经PID控制器仿真,并对比PID控制器的主要内容,如果未能解决你的问题,请参考以下文章
神经网络PID基于simulink的神经网络PID控制器仿真