统计学习方法与Python实现——k近邻法

Posted 2020-11-23 iwehdio

统计学*方法与Python实现（二）——k*邻法

　　iwehdio的博客园：https://www.cnblogs.com/iwehdio/

 

1、定义

　　k*邻法假设给定一个训练数据集，其中的实例类别已定。分类时，对新的实例，根据其k个最*邻的训练实例的类别，通过多数表决的方式进行预测。k*邻法不具有显式的学*过程，而实际上是利用训练数据集对特征空间进行划分，并作为其分类的模型。k*邻法的三个基本要素是 k值的选择、距离度量和分类决策规则。

　　k*邻法的模型是将特征空间划分成一些称为单元的子空间，并且每个单元内的点所属的类都被该单元的类标记所唯一确定。

　　单元的划分和类标记的确定需要首先对距离进行度量。特征空间中两个实例点的距离是它们之间相似程度的反映。对于n维实数向量的特征空间Rn，两向量xi和xj之间的Lp距离定义为：

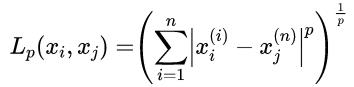　　当p=1时，称为曼哈顿距离：

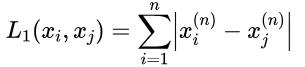
　　当p=2时，称为欧氏距离：

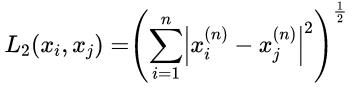
　　当p=∞时，取值为各个坐标距离的最大值：

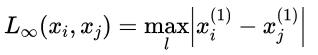
　　对于k值的选择，如果选择较小的k值，学*的*似误差会减小，但估计误差会增大，对噪声敏感。k值的减小就意味着整体模型变得复杂，容易发生过拟合。如果选择较大的k值，可以减少学*的估计误差，但缺点是学*的*似误差会增大。k值的增大 就意味着整体的模型变得简单。

　　在应用中，k值一般取一个较小的数值，并通过交叉验证法来确定最优的k值。

　　k*邻法中的分类决策规则往往是多数表决，即由输入实例的k个*邻的训练实例中的多数类决定输入实例的类。多数表决规则等价于经验风险最小化。

 

2、构造kd树

　　实现k*邻法是，主要的问题是如何对训练数据进行快速k*邻搜索。如果使用现行扫描，需要计算输入实例与每一个训练实例的距离，非常耗时。kd树是一种对k维空间中的实例 点进行存储以便对其进行快速检索的树形数据结构，可以提高搜索效率。

　　kd树是二叉树，表示对k维空间的一个划分。每次划分需要选定一个坐标轴和一个切分点，以此确定一个超平面对训练实例进行一次划分，并递归直到将实例划分完全。如果切分点每次*似选为该坐标轴上的中位数，则称这样的kd树为平衡kd树，算法流程如下：

　　a、构造根结点，其对应于包含整个训练实例T的k维空间。选择x1作为坐标轴，以T中所有实例的x1坐标的中位数作为切分点，切分由通过切分点并与x1轴垂直的超平面实现。由根节点生成深度为1的左右结点，左子结点对应于x1坐标小于切分点的子区域，右子结点对应于x1坐标大于切分点的子区域。落在切分超平面上的实例被保存在根结点。

　　b、递归重复。对于深度为 j 的结点，选择xn作为切分的坐标轴，其中n = ( j mod k) + 1，以节点区域中所有实例的xn坐标的中位数作为切分点。其他与a步中相同。

　　c、到两个子区域都没有实例点存在时停止，从而形成kd树的区域划分。

 

3、搜索kd树

　　完成对kd树的构造后，对于输入的测试实例，需要对kd树进行搜索，以得到输入实例的类别。以k=1的最*邻为例。给定输入实例，搜索最*邻。首先找到包含目标点的叶结点，其对应于包含目标点的最小子区域。以此叶结点的实例作为当前最*点，则目标点的最*邻一定在以目标点为中心，并通过当前最*点的超球体内部。然后返回当前节点的父结点，如果父结点的另一子结点的子区域与超球体相交，则在此子区域内寻找与目标点更*的实例点。如果存在这样的点，将此点作为新的当前最*点。返回更上一级的父结点，继续上述过程，直到父节点的另一子结点的子区域与超球体不相交，即不存在更*的点。算法流程如下：

　　a、从根结点出发，向下访问kd树，找到子区域包含输入实例的叶结点。

　　b、以此叶结点作为当前最*点。

　　c、递归的向上回退。如果该结点保存的实例点比当前最*点更*，则将此结点更新为当前最*点。如果以目标点为中心，通过当前最*点的的超球体与当前最*点的父结点的另一个子节点对应的子区域相交，则在此子区域中进行搜索与更新。如果不相交，则向上回退。

　　d、当回退到根结点时，搜索结束。当前最*点即为最*邻点。

 

 4、kd树的构造的Python实现

　　用到的数据集是sk-learn中的iris鸢尾花卉数据集，共150个数据，分为\'setosa\', \'versicolor\', \'virginica\'三类，数据包含四个特征sepal length（花萼长度）、sepal width（花萼宽度）、petal length（花瓣长度）和petal width（花瓣宽度）。

　　本次先从k=1的最*邻法实现k*邻。

　　首先，载入数据集并划分训练集和测试集。

from binarytree import *
import numpy as np
from sklearn.datasets import load_iris

# 从sk-learn库载入iris数据集
iris = load_iris()
# dict_keys([\'data\', \'target\', \'target_names\', \'DESCR\', \'feature_names\', \'filename\'])
# \'target_names\': array([\'setosa\', \'versicolor\', \'virginica\']

# 设定训练集和测试集大小
train_length = 105
test_length = 45

data = iris[\'data\']       # shape = (150, 4)
label = iris[\'target\']    # 0:50,0; 50:100,1; 100:150,2

train_data = np.zeros([train_length, 4])
train_label = np.zeros([train_length])
test_data = np.zeros([test_length, 4])
test_label = np.zeros([test_length])

# 划分训练集和测试集
length = train_length
for j in range(3):
    train_data[j * int(length/3):(j+1) * int(length/3)] = data[j*50:j*50 + int(length/3)]
    train_label[j * int(length/3):(j+1) * int(length/3)] = label[j*50:j*50 + int(length/3)]

length = test_length
for j in range(3):
    test_data[j * int(length/3):(j+1) * int(length/3)] = data[(j+1) * 50 - int(length/3):(j+1) * 50]
    test_label[j * int(length/3):(j+1) * int(length/3)] = label[(j+1) * 50 - int(length/3):(j+1) * 50]

train_index = np.arange(train_length).reshape([train_length, 1])
train_data = np.hstack((train_data, train_index))

　　

　　然后，构造kd树，二叉树由binarytree库实现。构造策略是，每次将数据四个特征中方差最大的轴作为划分轴，将该轴上特征值小于等于中位数的数据划分到左子树，大于中位数的数据划分到右子树。并记录每次划分时的轴和中位数值。

# 生成kd树
def creat_kd_tree(data, root, turn, log):

    axis = selct_axis(data[:, :-1])
    data = data[data[:, axis].argsort()]    # 按第axis列排序
    mid = data[:, axis].shape[0] // 2
    # 如果多个值在axis上的值与mid_data相同，则全部划分到左结点
    while mid < data.shape[0]-1 and data[mid + 1, axis] == data[mid, axis]:
        mid += 1
    mid_data = data[mid]
    log[int(mid_data[-1])] = (axis, mid_data[axis])
    # 存储左右子树下的结点
    data_left, data_right = [], []
    for temp in data[:mid]:
        data_left.append(temp)
    for temp in data[mid + 1:]:
        data_right.append(temp)
    # 创建新结点并递归
    node = Node(int(mid_data[-1]))
    # print(mid_data[-1], data_left, data_right)
    if turn: root.right = node
    else: root.left = node
    if data_left:
        creat_kd_tree(np.array(data_left), node, 0, log)
    if data_right:
        creat_kd_tree(np.array(data_right), node, 1, log)


# 选择方差最大的轴作为划分对象
def selct_axis(data, num=4):

    index = 0
    all_var = 0
    for i in range(num):
        axis_var = data[:, i].var()
        if all_var < axis_var:
            all_var = axis_var
            index = i
    return index


# kd树的根节点
node_init = Node(-1)
# log中保存了每个值为index的结点的超平面的轴和中位数值
log = [0 for i in range(train_length)]
creat_kd_tree(train_data, node_init, 0, log)
print(node_init.left)

 

 5、kd树的搜索的Python实现

 　　首先，寻找输入实例所属的子区域的叶节点，并记录路径。然后，根据记录的路径，从叶结点开始，计算以输入实例为球心，最*邻点距离为半径的超球体，与父结点的超平面有无交集。如果有交集，则遍历该父结点下的所有子结点，同时记录遍历过得结点防止重复计算。最后，返回模型中最*邻点的索引和距离。

# 寻找输入实例所属的子区域的叶节点，并记录路径
def find_leave(data, root, log):

    route = [(root.value, root)]
    while 1:
        index = root.value
        # print(index)
        if data[log[index][0]] <= log[index][1]:
            temp = root.left
        else:
            temp = root.right
        if temp is None:
            return route
        else:
            route.append((temp.value, temp))
            root = temp


# 寻找最*邻点
def find_neibor(simple, route, log):

    # 初始化最*邻点和距离
    near = route[-1][0]
    dst = np.linalg.norm((simple - train_data[near, :-1]))

    # 记录已经遍历过的结点
    save = []
    # 从后往前返回父结点
    for fa in route[:-1][::-1]:

        # 如果父结点的超平面与以输入实例为球心，最*邻点距离为半径的超球体有交集，则遍历其所有子结点
        if abs(log[fa[0]][1] - simple[log[fa[0]][0]]) < dst:
            child = []
            get_child(fa[1], child)
            for choic in child:
                if choic not in save:
                    dst0 = np.linalg.norm((simple - train_data[choic, :-1]))
                    save.append(choic)
                    if dst0 < dst:
                        dst = dst0
                        near = fa[0]
    return near, dst


# 返回父结点的所有子结点的值的列表
def get_child(root, child):

    if root is None:
        return 0
    else:
        child.append(root.value)
        get_child(root.left, child)
        get_child(root.right, child)

 　　

　　最后，在测试集上进行测试。

# 测试准确率
def acc(ans, label):

    counter = 0
    for index, num in enumerate(ans):
        if num == label[index]: counter += 1
    return counter / len(ans)


# 训练集
for n in range(train_length):
    valid_simple = train_data[n, :-1]
    rou = find_leave(valid_simple, node_init.left, log)
    valid_point, zero_true_distance = find_neibor(valid_simple, rou, log)
    # print(rou)
    # print(point, distance)

# 测试
ans = []
for n in range(test_length):
    test_simple = test_data[n]
    # rou记录了到输入实例叶结点的路径
    rou = find_leave(test_simple, node_init.left, log)
    test_point, test_distance = find_neibor(test_simple, rou, log)
    ans.append(train_label[test_point])
    # print(rou)
    print(test_point, test_distance, train_label[test_point])

print(\'test_acc\', acc(ans, test_label))

　　

　　在训练集上，每个输入都可以找到自己对应距离为0的结点。在测试集中，准确率为1，部分测试结果如下。第一列为最*邻点的索引，第二列为距离，第三列为分类结果。

 

 

6、其他问题

　　a、如何从k=1的最*邻法拓展到k为其他值下的k*邻法？

　　　　可以用长度为k的排序列表来实现。首先，先以关系最*的k个父结点和兄弟结点初始化排序列表。然后，按与最*邻法相同的算法，每次用排序列表中距离最大的值进行比较（也可能出现新值的距离比原来列表中的多个值都小的情况）。最后，当距离最大的值的超球体都与父结点的超平面无交集时，返回排序列表作为最*的k个值进行投票。

　　b、为什么用到超平面的距离代替超球体与其他结点的区域是否有交集？

　　　　因为计算点到区域的距离比较复杂，用到超平面的距离来代替超球体与超区域的问题是充分的，而且易于计算。

　　c、对于如手写数字集mnist类似的，数据值为0,1二值化的数据集，如何进行kd树的中位数划分？

　　　　可以每次在结点上任选一值为0的样本，然后将值为0的分到左子树，值为1的分为右子树，但是这样做并不能提高多少搜索效率。（所以用了iris...）

 

参考：李航 《统计学*方法（第二版）》

 

iwehdio的博客园：https://www.cnblogs.com/iwehdio/