R数据分析：生存数据的预测模型建立方法与评价

Posted 2023-04-18 Codewar

之前写了生存分析列线图的做法，列线图作为一个预测模型可视化工具，我们使用它的过程其实就是一个给新数据做预测的过程，其内在本身的模型就是我们基于现有数据训练的一个预测模型，今天也算是接着上一篇文章继续写生存分析的预测模型的效果评价。

生存数据预测模型和我们之前写的连续变量结局和分类结局的预测模型不同的地方就在于我们得考虑生存数据的删失和时间因素，通过这么一个预测模型，我们期望的目标是帮助临床医生去回答特定病人在某个时间的生存概率。从这个角度讲我们对模型评估和评价的标准就有一个锚定了。

Thus, survival prediction models differ from traditional prediction models for continuous or binary outcomes by appropriately accommodating censoring that is present in time-to-event data.to answer questions such as “What is the probability that this patient will be alive in 5 years, given their baseline covariate information?” This predicted probability can then be used by clinicians to make important decisions regarding patient care

比如说我收集了某个癌症病人的很大的有代表性的数据集，我通过我的数据学习出来了一个预测模型，再来一个新的癌症病人，模型可以告诉我，这个病人能活多久。

如果这个新数据本身有标签，我们通过对比实际标签（具体时间的生存概率）和模型预测结果（预测的具体时间的生存概率），就可以来评价模型优劣。逻辑和常规（分类结局和连续结局）的预测模型还是一样的。

先回顾生存分析

依然是先回顾下生存分析中的常见的术语：

 

我们的结局变量两个水平，一个是发生事件，另外一个是删失；同时这个结局还依赖于一个时间变量。

刚刚写了，我们做生存数据的预测，回答的是we are predicting the probability that an event happens at a particular time .----某个时刻发生事件的概率。所以这个时候常规的评价模型的指标都不好使了。

Due to the presence of the censoring in survival data, the standard evaluation metrics for regression such as root of mean squared error and ܴ R2 are not suitable for measuring the performance in survival analysis.

对于生存数据的预测模型，此时的评估模型的指标有下面3个：Concordance index (C-index)，Brier score，Mean absolute error。今天的任务就是一个一个带大家捋一遍，希望能帮助大家理解在“个体特定时间的生存概率这个锚定标准下，这些指标为什么可以用来评价模型。”

Concordance index (C-index)

首先看C指数，这个一致性指数在分类结局的预测模型中给大家提到过，就是ROC曲线下面积，对于生存数据的预测模型来讲，这个指数和灵敏度特异度就没关系了，它比的是实际值和预测值的排序一致不一致。理解方法可以参考秩和检验。

For a binary outcome, C-index is identical to the area under the ROC curve (AUC).

The concordance index or C-index is a generalization of the area under the ROC curve (AUC) that can take into account censored data. It represents the global assessment of the model discrimination power.

其逻辑在于：每个个案通过模型都给它一个风险分，如果模型表现好，那么风险分高的个案应该会先发生事件，按照这个逻辑，然后我们用模型给每个个案都赋一个风险分，形成很多个可以对比的组（2个为一组）：在组内确实满足刚刚讲的“风险分越大，事件越先发生”那么这个组就是一致性的组，否则就是不一致的组，这样一致性的组占所有对比组的比例就是C-index：

指数的计算方法如下：

 

其中，分子上是一致性的组，分母是所有组。那么这个值就是越大越好。

 

上面就是生存分析预测模型评价中C-index的内在逻辑，大家作为应用型科研工作者关注逻辑就好，请自动忽略掉数学表达。

Brier score

再来看第二个评价指标，叫做Brier score。这个Brier score是个案在t时间的生存状态减去t时间的预测生存概率的差的平方的均值。

其可以用来评价模型的逻辑在于：如果我的模型真的可以很好的预测特定时刻的生存概率，那么对于某个时刻我的生存状态确实是1，那么模型应该说我此时的生存概率无限大；反之模型应该说我的生存概率无限小。

因为牵扯到具体时间，这个指标只能截一个时间点去看，其算法如下：

 

we found that BS depends on the selection of time point t. Generally, the median of the observation time is selected as the time point.

就是个案在t时间的生存状态减去t时间的预测生存概率的差，比如在t时间个案实际观测到的是死亡（取0），那么这时候模型预测的生存概率应该越小越好；t时间个案实际观测到的是存活（取1），那么这个时候模型预测的生存概率应该是越大越好；肯定是减了之后的差越小越好嘛，也就是这个Brier score越小越好，并且得小于0.25才说明这个模型好过瞎猜。但是这指标只能看某个时间点模型的预测准确性。

上面就是生存分析预测模型评价中Brier score的内在逻辑，大家作为应用型科研工作者关注逻辑就好，自动忽略掉数学表达。

Mean absolute error

MAE这个指标在连续变量结局的预测模型中也有的，指的是预测值和实际值的差的绝对值的和，在生存分析的预测模型中，就是实际生存时间和模型预测生存时间的差的绝对值的和。算法如下：

 

 

这个指标只考虑了非删失数据，实际中就用得比较少。基本不用管。

模型评价实操

解释完指标之后我们再看实操做法，依然我们选取 JAMA Surg.的文章做参考，文章名如下：

Hyder O, Marques H, Pulitano C, et al. A Nomogram to Predict Long-term Survival After Resection for Intrahepatic Cholangiocarcinoma: An Eastern and Western Experience. JAMA Surg. 2014;149(5):432–438. doi:10.1001/jamasurg.2013.5168

文章中对模型评估的方法学介绍如下：

 

可以看到，这篇文章报告了C指数，用自助抽样样本画了校准曲线，还进行了模型的验证。我们首先来看C指数的做法，文章中报告了C指数的值和置信区间：

Predictive accuracy (discrimination) of the final model was measured by calculating the Harrell C index, which was 0.692 (95% CI, 0.624-0.762).

如果你是用coxph函数跑模型，那么模型的输出结果中自动会出来C指数C指数的标准误的，如下图：

 

比如我们就单独想要这个指数，可以直接运行下面代码：

cindex(formula, data)

要得到C指数的置信区间的话就得求助concordance.index函数，代码如下：

concordance.index(predict(c),surv.time = dt,surv.event = e,method = "noether")

输出如下，有C指数，标准误和对应置信区间上下限：

 

看完了C指数的操作我们再看校准曲线的画法，论文中给到的校准曲线长这样：

 

首先我们来理解什么是校准曲线，上图中横轴是模型预测的生存概率，纵轴是实际的生存概率。图中还有一条灰色的虚线，代表预测概率和实际的生存概率一致，最理想的情况下校准曲线是一条对角线(预测概率等于实际概率)，我们实际写文章的时候只要看着不要偏太离谱就行。

Calibration plot is a visual tool to assess the agreement between predictions and observations in different percentiles (mostly deciles) of the predicted values.

还要理解的是我们本身生存概率的分布是连续的，而图中只是画了3个点，这是因为算法将数据进行了分箱处理，上图中就是将原始数据分成了3组，这个操作使用calibrate函数中的参数m进行控制

For survival models, "predicted" means predicted survival probability at a single time point, and "observed" refers to the corresponding Kaplan-Meier survival estimate, stratifying on intervals of predicted survival。

同时，对于生存数据我们本身做预测的时候也是需要限定时间的，所以需要设定参数u。

比如我们要自助抽样20次，数据分箱，每箱200个，做时间点6的校准曲线的示例代码如下：

cal <- calibrate(f, u=6, cmethod=\'KM\', m=200, B=20)
plot(cal)

关于模型验证的结果，论文中通过报告重复抽样验证结果中训练数据和测试数据的C指数说明了模型并没有过拟合，原文如下：

Bootstrap validation of the model with 300 iterations revealed minimal evidence of model overfit. The training data set C statistic was 0.699, and the testing data set C statistic was 0.706, which represented the bias-corrected estimate of model performance in the future.

此部分的实现代码如下：

validate(f, B=300) 

通过输出结果中便可推算出相应数据集的C指数。

 

D_xy are equal to 2 * (C - 0.5)where C is the C-index or concordance probability

然后我们再对比下训练数据和测试数据的C指数的差异就可以去得到我们自己模型的结论。

好了，到这儿本期按照JAMA surgery文章给大家写的生存数据预测模型的做法与评价方法就给大家写完了，其实生存数据的预测模型还有别的评价方法比如时间依赖的ROC，决策曲线等等，安排在下期，请持续关注。

评价分类与预测算法的指标

　　分类与预测模型对训练集进行预测而得出的准确率并不能很好地反映预测模型未来的性能，为了有效判断一个预测模型的性能表现，需要一组没有参与预测模型建立的数据集，并在该数据集上评价预测模型的准确率，这组独立的数据集叫做测试集。模型预测效果评价，通常用相对/绝对误差、平均绝对误差、均方误差、均方根误差、平均绝对百分误差等指标来衡量。

1、绝对误差与相对误差

　　设$Y$表示实际值，$\\hatY$表示预测值，则$E$为绝对误差，其计算公式为：$E=Y-\\hatY$

　　$e$为相对误差，其计算公式为：$e=\\fracY-\\hatYY$

2、平均绝对误差

　　平均误差的计算公式为：$MAE=\\frac1n \\sum_i=1^n\\left|E_i\\right|=\\frac1n \\sum_i=1^n\\left|Y_i-\\hatY_i\\right|$

　　其中，$MAE$表示平均绝对误差，$E_i$表示第$i$个实际值与预测值的绝对误差，$Y_\\mathrmi$表示第$i$个实际值，$\\hatY_i$表示第$i$个预测值。

　　由于预测误差有正有负，为了避免正负相抵消，故取误差的绝对值进行综合并取其平均数，这是误差分析的综合指标法之一。

3、均方误差

　　均方误差的计算公式为：$MSE=\\frac1n \\sum_i=1^n E_i^2=\\frac1n \\sum_i=1^n\\left(Y_i-\\hatY_i\\right)^2$

　　其中，MSE表示均方差。均方误差一般用于还原平方失真程度。均方误差是预测误差平方之和的平均数，它避免了正负误差不能相加的问题。

　　由于对误差E进行了平方，加强了数值大的误差在指标中的作用，从而提高了这个指标的灵敏性，是一大优点。均方误差是误差分析的综合指标之一。

4、均方根误差

　　均方根误差的计算公式为：$RMSE=\\sqrt\\frac1n \\sum_i=1^n E_i^2=\\sqrt\\frac1n \\sum_i=1^n\\left(Y_i-\\hatY_i\\right)^2$

　　其中，RMSE表示均方根误差，其他符号同前。

　　这是均方误差的平方根，代表了预测值的离散程度，也叫标准误差，最佳拟合情况为$RMSE$=0。均方根误差也是误差分析的综合指标之一。

5、平均绝对百分误差

　　平均绝对百分误差为：$MAPE=\\frac1n \\sum_i=1^n\\left|E_i / Y_i\\right|=\\frac1n \\sum_i=1^n\\left|\\left(Y_i-\\hatY_i\\right) / Y_i\\right|$

　　其中，MAPE表示平均绝对百分误差。一般认为MAPE小于10时，预测精度较高。

6、Kappa统计

　　Kappa统计是比较两个或多个观测者对同一事物，或观测者对同一事物的两次或多次观测结果是否一致，是以由于机遇造成的一致性和实际观测的一致性之间的差别大小作为评价基础的统计指标。Kappa统计量和加权Kappa统计量不但可以用于无序和有序分类变量资料的一致性、重现性检验，而且能给出一个反映一致性大小的“量”值。

　　Kappa取值在[-1，+1]之间，其值的大小均有不同的意义：

　　　　Kappa=+1，说明两次判断的结果完全一致。

　　　　Kappa=-1，说明两次判断的结果完全不一致。

　　　　Kappa=0，说明两次判断的结果是机遇造成的。

　　　　Kappa<0，说明一致程度比机遇造成的还差，两次检查结果很不一致，在实际应用中无意义。

　　　　Kappa>0，说明有意义，Kappa越大，说明一致性愈好。

　　　　Kappa≥0.75，说明已经取得了相当满意的一致程度。

　　　　Kappa<0.4，说明一致程度不够。

7、识别准确度

 　　识别精确度的计算公式为：$\\text Accuracy=\\fracT P+F NT P+T N+F P+F N \\times 100 \\%$

　　其中各项的含义：

　　TP（True Positives）：正确的肯定，表示正确肯定的分类数。

　　TN（True Negatives）：正确的否定，表示正确否定的分类数。

　　FP（False Positives）：错误的肯定，表示错误肯定的分类数。

　　FN（False Negatives）：错误的否定，表示错误否定的分类数。

8、识别精确率

　　识别精确率的计算公式为：$\\text Precision =\\fracT PT P+F P \\times 100 \\%$

9、反馈率

　　反馈率的计算公式为：$\\text Recall=\\fracT PT P+T N \\times 100 \\%$

10、ROC曲线

　　受试者工作特性（Receiver Operating Characteristic，ROC）曲线，得此名的原因在于曲线上各点反映着相同的感受性，它们都是对同一信号刺激的反应，只不过是在几种不同的判定标准下所得的结果而已。接受者操作特性曲线就是以虚惊概率为横轴，击中概率为纵轴所组成的坐标图，和被试在特定刺激条件下由于采用不同的判断标准得出的不同结果画出的曲线。

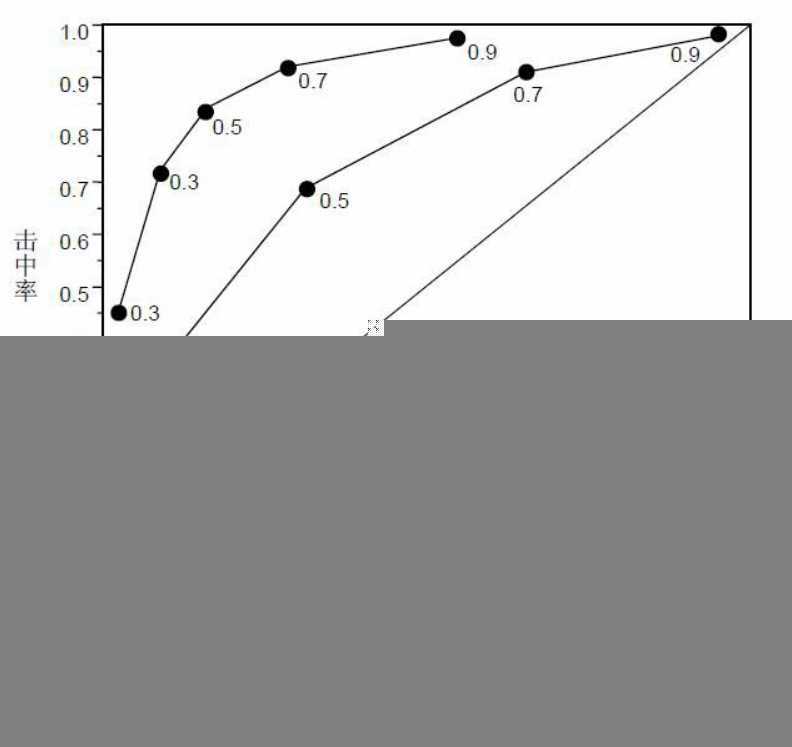
　　这是一种非常有效的模型评价方法，可为选定临界值给出定量提示。将灵敏度（Sensitivity）设在纵轴，1-特异性（1-Specificity）设在横轴，就可得出ROC曲线图。该曲线下的积分面积（Area）大小与每种方法的优劣密切相关，反映分类器正确分类的统计概率，其值越接近1说明该算法的效果越好。

11、混淆矩阵

　　混淆矩阵（Confusion Matrix）是模式识别领域中一种常用的表达形式。它描绘样本数据的真实属性与识别结果类型之间的关系，是评价分类器性能的一种常用方法。假设对于N类模式的分类任务，识别数据集D包括$T_0$个样本，每类模式分别含有$T_i$个数据（i=1…N）。采用某种识别算法构造分类器$C$，$c m_i j$，表示第$i$类模式被分类器$C$判断成第$j$类模式的数据占第$i$类模式样本总数的百分率，则可得到如下N·N维混淆矩阵：$$C M(C, D)=\\left(\\beginarraycccccc m_11 & c m_22 & \\dots & c m_1 i & \\dots & c m_1 N \\\\ c m_21 & c m_22 & \\dots & c m_2 i & \\dots & c m_2 N \\\\ \\vdots & \\vdots & & \\vdots & \\\\ c m_i 1 & c m_i 2 & \\dots & c m_i i & \\dots & c m_i N \\\\ \\vdots & \\vdots & & \\vdots & \\\\ c m_N 1 & c m_N 2 & \\dots & c m_N i & \\dots & c m_N N\\endarray\\right)$$

　　混淆矩阵中元素的行下标对应目标的真实属性，列下标对应分类器产生的识别属性。对角线元素表示各模式能够被分类器C正确识别的百分率，而非对角线元素则表示发生错误判断的百分率。

　　通过混淆矩阵，可以获得分类器的正确识别率和错误识别率。

　　各模式正确识别率：$R_i=c m_i i, \\quad i=1, \\cdots, N$

　　平均正确识别率：$R_A=\\sum_i=1^N\\left(c m_i i \\cdot T_i\\right) / T_0$

　　各模式错误识别率：$W_i=\\sum_j=1, j \\neq i^N c m_i j=1-c m_i i=1-R_i$

　　平均错误识别率：$W_A=\\sum_i=1^N \\sum_j=1, j \\neq i^N\\left(c m_i i \\cdot T_i\\right) / T_0=1-R_A$