142. 环形链表 II

Posted 2023-04-07 luxiayuai

 

解法一：①首先判断是否有环，若无环，则快指针或其下一指针指向空；若有环，则从快慢指针相遇的位置继续出发，直到再次相遇，遍历次数即为环长len。②两指针从头结点重新开始，让其中一指针先出发len步，而后另一指针再出发，相遇节点即为环起点。

/**
 * Definition for singly-linked list.
 * struct ListNode 
 *     int val;
 *     ListNode *next;
 *     ListNode(int x) : val(x), next(NULL) 
 * ;
 */
class Solution 
public:
    ListNode *detectCycle(ListNode *head) 
        if(head == NULL || head->next == nullptr) return nullptr;
        ListNode* fast = head;
        ListNode*slow = head;
        while(fast != nullptr && fast->next != nullptr)
            fast = fast->next->next;
            slow = slow->next;
            if(fast == slow) break;
        

        if(fast == nullptr || fast->next == nullptr) return nullptr;

        //快慢重新出发，再次相遇时slow所走步数为环长len
        fast = fast->next->next;
        slow = slow->next;
        int len = 1;
        while(fast != slow)
            fast = fast->next->next;
            slow = slow->next;
            ++ len;
        
        //二指针回头节点，快指针先走环长len
        fast = head;
        slow = head;
        for(int i = 0; i < len; i ++ )
            fast = fast->next;
        
        while(fast != slow) 
            fast = fast->next;
            slow = slow->next;
        
        return fast;
    
;

 解法二：优化的版本。x表示链表头到环起点距离，首次判环相遇点必然距环起点x。另其中一指针从头节点重开，同步同速启动直到相遇即可。

这里有点绕。

详细解释：假定链表起点到入环的第一个节点A的长度为a【未知】，到快慢指针相遇的节点B的长度为（a + b）【这个长度是已知的】。现在我们想知道a的值，注意到快指针p2始终是慢指针p走过长度的2倍，所以慢指针p从B继续走（a + b）又能回到B点，如果只走a个长度就能回到节点A。（假设环内剩余长度为c,则快指针走过的长度为: 2(a+b) = a + b + c + b 所以c=a）

注意一个容易忽略的点，当环非常小而链表非常长时存在快指针在环中遍历不止一次的情况，这样的话上面的a和b存在对环长取余的情况，不过不影响结果。

/**
 * Definition for singly-linked list.
 * struct ListNode 
 *     int val;
 *     ListNode *next;
 *     ListNode(int x) : val(x), next(NULL) 
 * ;
 */
class Solution 
public:
    ListNode *detectCycle(ListNode *head) 
        if(head==nullptr || head->next == nullptr) return nullptr;
        ListNode* fast = head;
        ListNode* slow = head;
        while(fast != NULL && fast->next != nullptr)
            fast = fast->next->next;
            slow = slow->next;
            if(fast == slow) break;
        
        if(fast == nullptr || fast->next == nullptr) return nullptr;

        fast = head;
        while(fast != slow)
            //slow在环内距起点x+cnt*环长，fast在链表头也距环起点x，同步，相遇。
            fast = fast->next;
            slow = slow->next;
        
        return fast;
    
;

 

LeetCode Java刷题笔记—142. 环形链表 II

142. 环形链表 II

给定一个链表，返回链表开始入环的第一个节点。 如果链表无环，则返回 null。不允许修改链表结构。这道题是141. 环形链表的延伸。

在做这道题之前，应该先做LeetCode Java刷题笔记—141. 环形链表。

先放代码，下面进行推导：

/**
 * 142. 环形链表 II
 * 给定一个链表，返回链表开始入环的第一个节点。 如果链表无环，则返回 null。不允许修改链表。
 * https://leetcode-cn.com/problems/linked-list-cycle-ii/
 * 中等
 */
public class LeetCode142 

    public ListNode detectCycle(ListNode head) 
        ListNode slow = head;
        ListNode fast = head;
        boolean hasCycle = false;
        while (fast != null && fast.next != null) 
            slow = slow.next;
            fast = fast.next.next;
            if (slow == fast) 
                hasCycle = true;
                break;
            
        
        if (hasCycle) 
            while (head != slow) 
                head = head.next;
                slow = slow.next;
            
            return slow;
        
        return null;
    

    public class ListNode 

        int val;
        ListNode next;

        ListNode() 

        

        ListNode(int val) 

            this.val = val;
        

        ListNode(int val, ListNode next) 

            this.val = val;
            this.next = next;
        
    

假设已经证明了链表有环，我们目前仅能够得知相遇节点为s，头节点为h，其他的一概不知。

设头节点h到环入口节点长x，相遇节点s到环入口长a，相遇的时候slow节点在环内走过的长度为b，环长度为y。那么y=a+b。

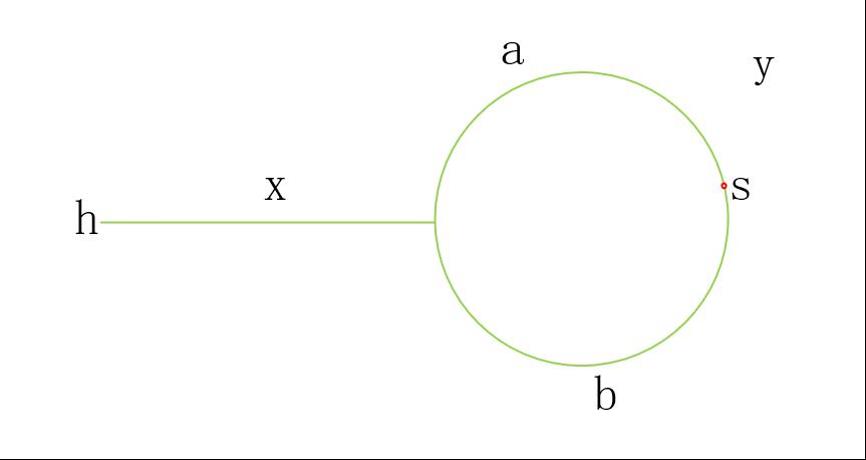
那么，相遇时slow走过的长度为x+b，fast走过的长度为x+n(a+b)+b

由于fast是slow速度的二倍，那么距离也是二倍，那么2(x+b)=x+n(a+b)+b，我们来对这个的等式进行转换：

2(x+b)=x+n(a+b)+b
2x+2b=x+na+(n+1)b
2x=x+na+(n-1)b
x=na+(n-1)b
x=(n-1)(a+b)+a
x=(n-1)y+a

结果已经呼之欲出了，由于y的长度就是一圈的长度，因此，无论(n-1)y的结果是多少，最终都会是环长度的整数倍，从s节点出发，最终都会回到节点s，那么如果再走过a的距离，实际上s节点就到了环节点的入口，另一方面如果我们从头节点h开始走，经过x的距离时同样可以到达环节点的入口。

那么我们使用相遇节点s和头节点h同时出发，每次都走一步，当他们指向的节点相等时，那就是他们都走到了环节点的入口节点：

        if (hasCycle) 
            while (slow != head) 
                head = head.next;
                slow = slow.next;
            
            return head;
        

发散思维：如何求环长度呢？很简单，我们让fast在相遇点不动，然后slow从该节点出发单独去走一圈，直到再碰到fast节点，此过程中走过的路程就是环长度。