ABC295（D~G）

Posted 2023-04-02 LuoyuSitfitw

Tasks - AtCoder Beginner Contest 295

这篇是超级抽象的简要tj，看不懂不要骂我这个蒟蒻QWQ

D - Three Days Ago (atcoder.jp)

\\(f_i\\)表示\\([1,i]\\)的所有数的奇偶情况，如果\\(b\\)有奇数个，那么\\(f_i|=2^b\\)，特别的，\\(f_0=0\\)，答案就是\\(\\sum\\limits_i=1^n \\sum\\limits_j=0^i-1 [f_j=f_i]\\)

#include<bits/stdc++.h>
#define ll long long
using namespace std;
const int N=5e5+5;
int n,f[N];
char s[N];
map<int,int> mp;
ll ans;
int main()
	scanf("%s",s+1);
	n=strlen(s+1);
	++mp[0];
	for(int i=1;i<=n;++i) f[i]=f[i-1],f[i]^=(1<<(int)(s[i]-\'0\'));
	for(int i=1;i<=n;++i) ans+=mp[f[i]],++mp[f[i]];
	printf("%lld\\n",ans);


	return 0;

E - Kth Number (atcoder.jp)

最后的答案为\\(\\sum\\limits_i=1^m i*\\i作为A_k的概率\\\\)，就相当于求\\(\\sum\\limits_i=1^m \\A_k\\geq i的概率\\\\)

#include<bits/stdc++.h>
using namespace std;
const int N=2e3+5,MOD=998244353;
int n,m,k,a[N],C[N][N],ans,p[N],q[N]; 
void Init()
	for(int i=0;i<=n;++i)
		C[i][0]=1;
		for(int j=1;j<=i;++j) C[i][j]=(1ll*C[i-1][j]+1ll*C[i-1][j-1])%MOD;
	

int power(int x,int y)
	int ans=1;
	for(;y;y>>=1,x=1ll*x*x%MOD) if(y&1) ans=1ll*ans*x%MOD;
	return ans;

int main()
	scanf("%d%d%d",&n,&m,&k),Init();
	for(int i=1;i<=n;++i) scanf("%d",&a[i]); 
	for(int i=1;i<=m;++i)
		int nd=n+1-k,cnt=0;
		for(int j=1;j<=n;++j) nd-=(a[j]>=i),cnt+=(!a[j]);
		if(nd<0||nd>cnt)
			if(nd<0) ans=(ans+1ll)%MOD;
			continue;
		
		int pp=1ll*(m-i+1)*power(m,MOD-2)%MOD,qq=(MOD+1-pp)%MOD;
		p[0]=q[0]=1;
		for(int j=1;j<=cnt;++j) p[j]=1ll*p[j-1]*pp%MOD,q[j]=1ll*q[j-1]*qq%MOD;
		for(int j=nd;j<=cnt;++j) ans=(1ll*ans+1ll*C[cnt][j]*p[j]%MOD*q[cnt-j]%MOD)%MOD;
	
	printf("%d",ans);
	return 0;

F - substr = S (atcoder.jp)

答案肯定是\\(ask(r)-ask(l-1)\\)

枚举\\(S\\)处于当前数字的位置，如果现在给一个排名\\(k\\)，那么我们就可以根据这个排名得出当前数字应该是多少

所以考虑\\(S\\)所处的位置下的最大排名，也就是最大个数，最后答案就是所有位置下的个数的和

#include<bits/stdc++.h>
#define int long long
using namespace std;
string s;
int l,r,pw[20];
int ask(int i,int k,string s)
	int a=s.size(),b=k-a+1;
	if(b<0) return -1;
	--i;
	if(s[0]==\'0\') i+=pw[b];
	int x=i/pw[b],y=i%pw[b];
	return x*pw[k+1]+stoll(s)*pw[b]+y;

int ans;
int solve(int x,string s)
	ans=0;
	for(int k=0;k<=15;++k)
		int t=ask(1,k,s);
		if(t==-1||t>x) continue;
		int l=0,r=pw[16-s.size()],mid;
		while(l<r)
			mid=l+r+1>>1;
			if(ask(mid,k,s)>x) r=mid-1;
			else l=mid;
		
		ans+=r;
	
	return ans;

signed main()
	int T; scanf("%lld",&T);
	pw[0]=1; for(int i=1;i<=17;++i) pw[i]=pw[i-1]*10;
	while(T--)
		cin>>s>>l>>r;
		printf("%lld\\n",solve(r,s)-solve(l-1,s));	
	
	return 0;

G - Minimum Reachable City (atcoder.jp)

可以发现，连了一条边过后会构成一个环，环上的点在一条链上，并且环上所有点的答案都跟新为这个环上深度最浅的点的答案

所以自然而然就想到并查集，也就是将环上所有点都连向最浅的点，因为环上的点一定在一条链上，所以如果下次构成的环经过了这个环的点，那么就可以直接跳过这些点，跳到这个环上所有的点的指向的点\\(x\\)上去，此时，要么下次构成的环的最高的点\\(y\\)也指向\\(x\\)，这个就不用管；要么就是\\(x\\)指向\\(y\\)。

#include<bits/stdc++.h>
#define pb push_back
using namespace std;
const int N=2e5+5;
int n;
vector<int> edge[N];
int ans[N],fa[N],fr[N];
void dfs(int u)
	ans[u]=u,fa[u]=u;
	for(auto v:edge[u])
		dfs(v);
		ans[u]=min(ans[u],ans[v]);
	

int find(int x)
	if(fa[x]==x) return x;
	return fa[x]=find(fa[x]);

int main()
	scanf("%d",&n);
	for(int i=2,u,v;i<=n;++i) scanf("%d",&fr[i]),edge[fr[i]].pb(i);
	dfs(1);
	int q,op,u,v; scanf("%d",&q);
	while(q--)
		scanf("%d%d",&op,&u);
		if(op==1)
			scanf("%d",&v),v=find(v);
			while(u!=v)
				u=find(u);
				if(u==v) continue;
				fa[u]=v,u=fr[u];
			
		else printf("%d\\n",ans[find(u)]);
	

	return 0;

ABC206 E - Divide Both（容斥）

题意：

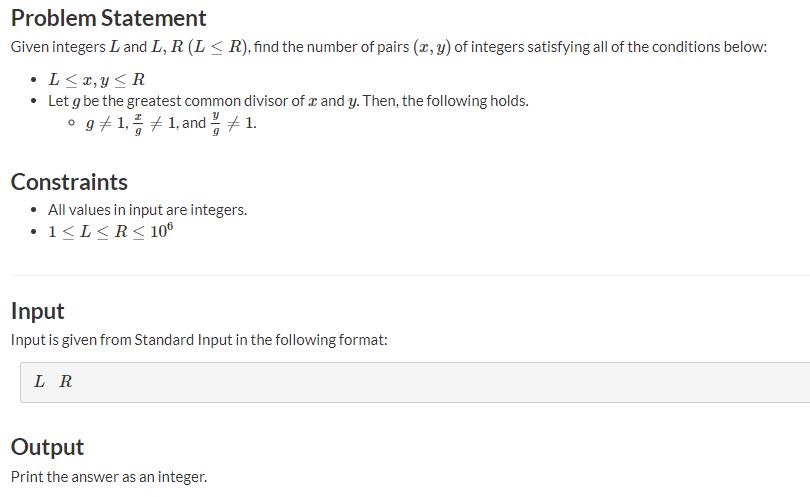
解法：

考虑枚举gcd=i,计算gcd=i的数对数量(先不考虑g!=x和g!=y的这个条件),
然后减去不合法条件(即g=x或者g=y的情况),

令d[i]为gcd=i的数对数量,可以容斥计算:
d[i]=[r/i-(l-1)/i]^2-d[i*2]-d[i*3]....

先ans+=sum{d[2,r]}.

由于需要减去g=x或者g=y的情况,
枚举g=[max(2,l),r],
那么ans-={数对(g,kg)的数量}+{数对(kg,g)的数量}+{(g,g)的数量},
其中k>=1,设cnt=r/i-(l-1)/i,容易得出上式可以转化为ans-=cnt*2+1.

code：

#include<bits/stdc++.h>
#define int long long
using namespace std;
const int maxm=4e6+5;
int d[maxm];
void solve(){
    int l,r;cin>>l>>r;
    for(int i=r;i>=1;i--){
        int cnt=r/i-(l-1)/i;
        d[i]=cnt*cnt;
        for(int j=i+i;j<=r;j+=i){
            d[i]-=d[j];
        }
    }
    int ans=0;
    for(int i=2;i<=r;i++){//枚举g
        ans+=d[i];
        if(i>=l&&i<=r){
            int cnt=r/i-(l-1)/i;
            ans-=cnt*2-1;
        }
    }
    cout<<ans<<endl;
}
signed main(){
    ios::sync_with_stdio(0);cin.tie(0);
    solve();
    return 0;
}

---