Python实现数值计算----牛顿插值法
Posted
tags:
篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了Python实现数值计算----牛顿插值法相关的知识，希望对你有一定的参考价值。
拉格朗日插值法的最大毛病就是每次引入一个新的插值节点，基函数都要发生变化，这在一些实际生产环境中是不合适的，有时候会不断的有新的测量数据加入插值节点集，
因此，通过寻找n个插值节点构造的的插值函数与n+1个插值节点构造的插值函数之间的关系，形成了牛顿插值法。推演牛顿插值法的方式是归纳法，也就是计算Ln（x）- Ln+1（x），并且从n=1开始不断的迭代来计算n+1时的插值函数。
牛顿插值法的公式是：
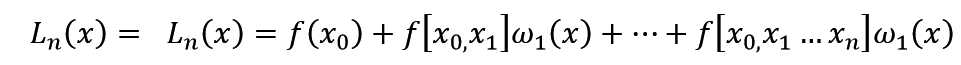
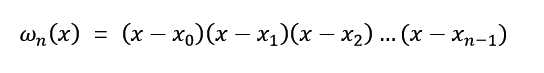
注意：在程序中我用W 代替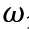 
计算牛顿插值函数关键是要计算差商，n阶差商的表示方式如下：
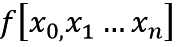
关于差商我在这里并不讨论
计算n阶差商的公式是这样：
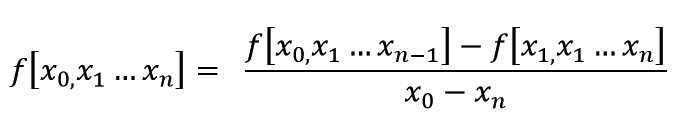
很明显计算n阶差商需要利用到两个n-1阶差商，这样在编程的时候很容易想到利用递归来实现计算n阶差商，不过需要注意的是递归有栈溢出的潜在危险，在计算差商的时候
更是如此，每一层递归都会包含两个递归，递归的总次数呈满二叉树分布：
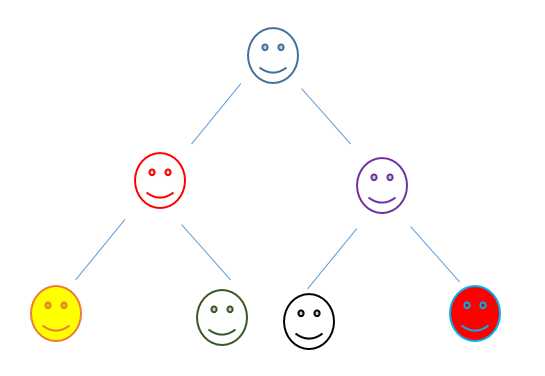
这意味着递归次数会急剧增加:(。所以在具体的应用中还需要根据应用来改变思路或者优化代码。
废话少说，放码过来。
首先写最关键的一步，也就是计算n阶差商：
"""
@brief: 计算n阶差商 f[x0, x1, x2 ... xn]
@param: xi 所有插值节点的横坐标集合 o
@param: fi 所有插值节点的纵坐标集合 / @return: 返回xi的i阶差商(i为xi长度减1) o o
@notice: a. 必须确保xi与fi长度相等 / \\ / b. 由于用到了递归，所以留意不要爆栈了. o o o o
c. 递归减递归(每层递归包含两个递归函数), 每层递归次数呈二次幂增长，总次数是一个满二叉树的所有节点数量(所以极易栈溢出)
"""
def get_order_diff_quot(xi = [], fi = []):
if len(xi) > 2 and len(fi) > 2:
return (get_order_diff_quot(xi[:len(xi) - 1], fi[:len(fi) - 1]) - get_order_diff_quot(xi[1:len(xi)], fi[1:len(fi)])) / float(xi[0] - xi[-1])
return (fi[0] - fi[1]) / float(xi[0] - xi[1])
看上面的牛顿插值函数公式，有了差商，还差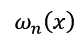
这个就比较好实现了：
"""
@brief: 获得Wi(x)函数;
Wi的含义举例 W1 = (x - x0); W2 = (x - x0)(x - x1); W3 = (x - x0)(x - x1)(x - x2)
@param: i i阶(i次多项式)
@param: xi 所有插值节点的横坐标集合
@return: 返回Wi(x)函数
"""
def get_Wi(i = 0, xi = []):
def Wi(x):
result = 1.0
for each in range(i):
result *= (x - xi[each])
return result
return Wi
OK， 牛顿插值法最重要的两部分都有了，下面就是将这两部分组合成牛顿插值函数，如果是c之类的语言就需要保存一些中间数据了，我利用了Python的闭包直接返回一个牛顿插值函数，闭包可以利用到它所处的函数之中的上下文数据。
"""
@brief: 获得牛顿插值函数
@
"""
def get_Newton_inter(xi = [], fi = []):
def Newton_inter(x):
result = fi[0]
for i in range(2, len(xi)):
result += (get_order_diff_quot(xi[:i], fi[:i]) * get_Wi(i-1, xi)(x))
return result
return Newton_inter
上面这段代码就是对牛顿插值函数公式的翻译，注意get_Wi函数的参数是i-1，这个从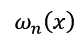函数的表达式可以找到原因。
构造一些插值节点
‘‘‘ 插值节点, 这里用二次函数生成插值节点，每两个节点x轴距离位10 ‘‘‘
sr_x = [i for i in range(-50, 51, 10)]
sr_fx = [i**2 for i in sr_x]
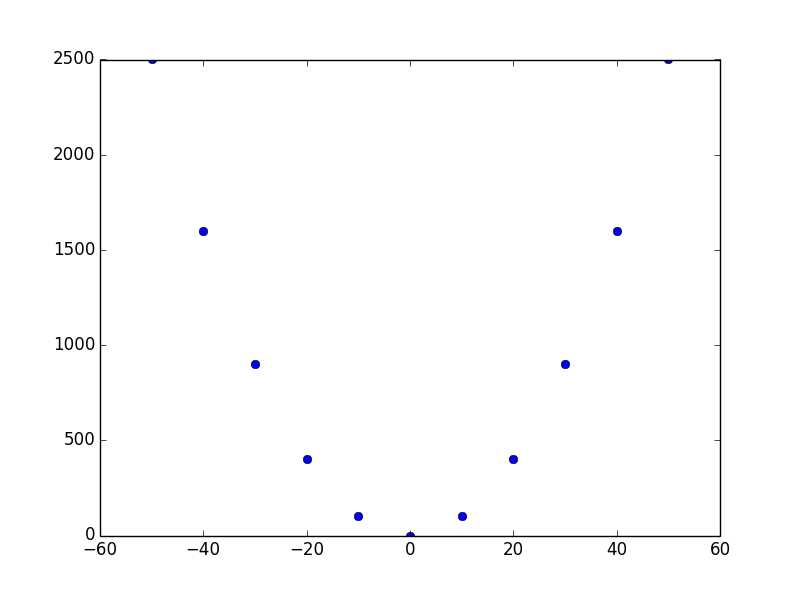
获得牛顿插值函数
Nx = get_Newton_inter(sr_x, sr_fx) # 获得插值函数
tmp_x = [i for i in range(-50, 51)] # 测试用例
tmp_y = [Nx(i) for i in tmp_x] # 根据插值函数获得测试用例的纵坐标
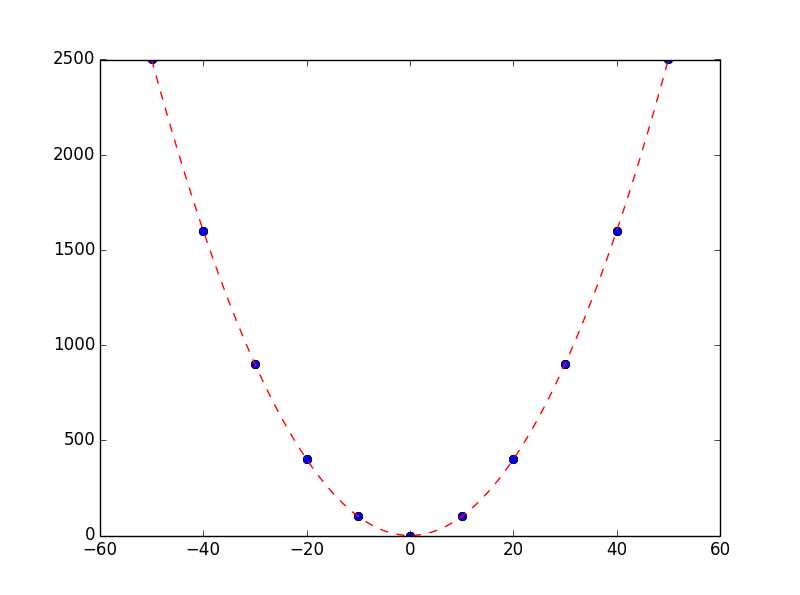
完整代码：
# -*- coding: utf-8 -*-
"""
Created on Thu Nov 17 18:34:21 2016
@author: tete
@brief: 牛顿插值法
"""
import matplotlib.pyplot as plt
"""
@brief: 计算n阶差商 f[x0, x1, x2 ... xn]
@param: xi 所有插值节点的横坐标集合 o
@param: fi 所有插值节点的纵坐标集合 / @return: 返回xi的i阶差商(i为xi长度减1) o o
@notice: a. 必须确保xi与fi长度相等 / \\ / b. 由于用到了递归，所以留意不要爆栈了. o o o o
c. 递归减递归(每层递归包含两个递归函数), 每层递归次数呈二次幂增长，总次数是一个满二叉树的所有节点数量(所以极易栈溢出)
"""
def get_order_diff_quot(xi = [], fi = []):
if len(xi) > 2 and len(fi) > 2:
return (get_order_diff_quot(xi[:len(xi) - 1], fi[:len(fi) - 1]) - get_order_diff_quot(xi[1:len(xi)], fi[1:len(fi)])) / float(xi[0] - xi[-1])
return (fi[0] - fi[1]) / float(xi[0] - xi[1])
"""
@brief: 获得Wi(x)函数;
Wi的含义举例 W1 = (x - x0); W2 = (x - x0)(x - x1); W3 = (x - x0)(x - x1)(x - x2)
@param: i i阶(i次多项式)
@param: xi 所有插值节点的横坐标集合
@return: 返回Wi(x)函数
"""
def get_Wi(i = 0, xi = []):
def Wi(x):
result = 1.0
for each in range(i):
result *= (x - xi[each])
return result
return Wi
"""
@brief: 获得牛顿插值函数
@
"""
def get_Newton_inter(xi = [], fi = []):
def Newton_inter(x):
result = fi[0]
for i in range(2, len(xi)):
result += (get_order_diff_quot(xi[:i], fi[:i]) * get_Wi(i-1, xi)(x))
return result
return Newton_inter
"""
demo:
"""
if __name__ == ‘__main__‘:
‘‘‘ 插值节点, 这里用二次函数生成插值节点，每两个节点x轴距离位10 ‘‘‘
sr_x = [i for i in range(-50, 51, 10)]
sr_fx = [i**2 for i in sr_x]
Nx = get_Newton_inter(sr_x, sr_fx) # 获得插值函数
tmp_x = [i for i in range(-50, 51)] # 测试用例
tmp_y = [Nx(i) for i in tmp_x] # 根据插值函数获得测试用例的纵坐标
‘‘‘ 画图 ‘‘‘
plt.figure("I love china")
ax1 = plt.subplot(111)
plt.sca(ax1)
plt.plot(sr_x, sr_fx, linestyle = ‘‘, marker=‘o‘, color=‘b‘)
plt.plot(tmp_x, tmp_y, linestyle = ‘--‘, color=‘r‘)
plt.show()
以上是关于Python实现数值计算----牛顿插值法的主要内容，如果未能解决你的问题，请参考以下文章