[数值计算-14]:拉格朗日插值与Python代码实现
Posted 文火冰糖的硅基工坊
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了[数值计算-14]:拉格朗日插值与Python代码实现相关的知识,希望对你有一定的参考价值。
作者主页(文火冰糖的硅基工坊):https://blog.csdn.net/HiWangWenBing
本文网址:https://blog.csdn.net/HiWangWenBing/article/details/119967939
目录
第1章 案例与建模
1.1 案例说明

1.2 建模与预测

第2章 插值
2.1 什么是插值


这里的插值条件是:插值函数要经过所有现有的样本点!!!
这个插值条件的优点:在样本点的误差为0。
这个插值条件的缺点:这个条件还是比较苛刻的,导致选用高次函数,且样本点的个数越多,函数的最高次的次数越高。
2.2 插值的关键是如何构建插值函数!!!


第3章 拉格朗日插值
有没有一种插值方法,不需要求解线性方程组,只需要对样本点数据进行数值计算,就可以获取插值函数,拉格朗日插值就是这样的一种插值方法。
3.1 拉格朗日插值的基本思想
假如有N+1个采样点,能否在每个采样点Xk处,都构建这样的一个n次多项式函数Lk(x),该该函数满足:
(1) 当i = k是,Lk(Xi) = Yi
(2) 当i != k是,Lk(Xi) = 0
这样,把所有点的n次多项式进行累加,这样就可以得到N+1个采样点的多项式插值函数。
其中Lk(x)为基函数,累计后的函数为插值函数
3.2 拉格朗日基函数

基函数的次数与采样点的个数有对应的关系,N+1点,基函数的次数就是N。
3.3 拉格朗日插值函数

插值函数是基函数的简单的线性相加。
3.3 拉格朗日2点插值公式拆解
(1)公式描述

(2)代码示例:2个采样点数据
#导入库
from math import *
import time
import numpy as np
import matplotlib.pyplot as plt
from pylab import mpl
print('两点插值的采样数据:')
x_samples_dot2 = [1, 2]#创建x列表存储数据x值
y_samples_dot2 = [4, 8]#创建y列表存储数据的y值
print("X:", x_samples_dot2)
print("Y:", y_samples_dot2)
plt.scatter(x_samples_dot2, y_samples_dot2, label="sample", color="black")
plt.plot (x_samples_dot2, y_samples_dot2, label="sample", color="red")
mpl.rcParams['font.sans-serif'] = ['SimHei'] #设置中文字体
mpl.rcParams['axes.unicode_minus'] = False
plt.title("Dot2 采样数据")
plt.legend(loc="upper left")
plt.show()输出:
两点插值的采样数据: X: [1, 2] Y: [4, 8]

(3)代码示例:两点插值的分解与叠加
# 插值基函数
#L0(x) = y0 * (x-x1)/(x0-x1)
def Dot2_L0(x, x_data,y_data):
return (y_data[0] * (x-x_data[1])/(x_data[0]-x_data[1]))
#L1(x) = y1 * (x-x0)/(x1-x0)
def Dot2_L1(x, x_data,y_data):
return (y_data[1] * (x-x_data[0])/(x_data[1]-x_data[0]))
# 插值函数:是基函数的线性叠加
def Dot2_F(x, x_data, y_data):
return (Dot2_L0(x, x_data,y_data) + Dot2_L1(x, x_data,y_data))
#基函数的预测
#输入x数据序列
x_data_predict_dot2 = np.arange(0, 3, 0.2)
#基函数L0的预测序列
y_data_predict_dot2_L0 = Dot2_L0(x_data_predict_dot2, x_samples_dot2, y_samples_dot2)
#基函数L1的预测序列
y_data_predict_dot2_L1 = Dot2_L1(x_data_predict_dot2, x_samples_dot2, y_samples_dot2)
#插值函数的预测序列
y_data_predict_dot2_F = Dot2_F(x_data_predict_dot2, x_samples_dot2, y_samples_dot2)
#显示基函数与插值函数的图形
plt.scatter(x_samples_dot2, y_samples_dot2, label="sample", color="black")#画点
plt.plot (x_data_predict_dot2, y_data_predict_dot2_L0, label="L0(x)", color="green")
plt.plot (x_data_predict_dot2, y_data_predict_dot2_L1, label="L1(x)", color="blue")#画点
plt.plot (x_data_predict_dot2, y_data_predict_dot2_F, label="f(x)", color="red")#画点
#设置属性
mpl.rcParams['font.sans-serif'] = ['SimHei']
mpl.rcParams['axes.unicode_minus'] = False
plt.title("Dot2 拉格朗日插值拟合过程")
plt.legend(loc="upper left")
plt.show()
输出结果:

从上述图形可以看出:
- 基函数L0(x) 是一条直线,且穿过(x0,y0)点。
- 基函数L1(x) 是一条直线,且穿过(x1,y1)点。
- 插值函数F(x) 是L0(x)和L1(x)的线性叠加,
- 插值函数F(x) 也是一条直线,且同时穿过(x0,y0)点和(x1,y1)点。
3.4 拉格朗日3点插值公式
(1)公式描述

(2)代码示例:样本点图形
print('三点插值的采样数据:')
x_samples_dot3 = [1, 2, 3]#创建x列表存储数据x值
y_samples_dot3 = [4, 8, 6]#创建y列表存储数据的y值
print("X:", x_samples_dot3)
print("Y:", y_samples_dot3)
plt.scatter(x_samples_dot3, y_samples_dot3, label="sample", color="black")#画点
plt.plot (x_samples_dot3, y_samples_dot3, label="sample", color="red")#画点
plt.title("Dot3 采样数据")
plt.legend(loc="upper left")
plt.show()
输出:
三点插值的采样数据: X: [1, 2, 3] Y: [4, 8, 6]

(3)代码示例:两点插值的分解与叠加
# 基函数
#L0(x) = y0 * ((x-x1)*(x-x2))/((x0-x1)*(x0-x2))
def Dot3_L0(x, x_data,y_data):
return (y_data[0] * ((x-x_data[1]) * (x-x_data[2]))/((x_data[0]-x_data[1]) * (x_data[0]-x_data[2])))
#L1(x) = y1 * ((x-x0)*(x-x2))/((x1-x0)*(x1-x2))
def Dot3_L1(x, x_data,y_data):
return (y_data[1] * ((x-x_data[0]) * (x-x_data[2]))/((x_data[1]-x_data[0]) * (x_data[1]-x_data[2])))
#L0(x) = y2 * ((x-x0)*(x-x1))/((x2-x0)*(x2-x1))
def Dot3_L2(x, x_data,y_data):
return (y_data[2] * ((x-x_data[0]) * (x-x_data[1]))/((x_data[2]-x_data[0]) * (x_data[2]-x_data[1])))
#插值函数:是基函数的线性叠加
def Dot3_F(x, x_data, y_data):
return (Dot3_L0(x, x_data,y_data) + Dot3_L1(x, x_data,y_data) + Dot3_L2(x, x_data,y_data))
##函数的预测:输入数据序列为x
x_data_predict_dot3 = np.arange(0, 4.2, 0.2)
#基函数L0的预测序列
y_data_predict_dot3_L0 = Dot3_L0(x_data_predict_dot3, x_samples_dot3, y_samples_dot3)
#基函数L1的预测序列
y_data_predict_dot3_L1 = Dot3_L1(x_data_predict_dot3, x_samples_dot3, y_samples_dot3)
#基函数L2的预测序列
y_data_predict_dot3_L2 = Dot3_L2(x_data_predict_dot3, x_samples_dot3, y_samples_dot3)
#插值函数的预测序列
y_data_draw_dot3_F = Dot3_F (x_data_predict_dot3, x_samples_dot3, y_samples_dot3)
#显示基函数与插值函数的关系
plt.scatter(x_samples_dot3, y_samples_dot3, label="sample", color="black")
plt.plot (x_data_predict_dot3, y_data_predict_dot3_L0, label="L0(x)", color="green")
plt.plot (x_data_predict_dot3, y_data_predict_dot3_L1, label="L1(x)", color="blue")
plt.plot (x_data_predict_dot3, y_data_predict_dot3_L2, label="L2(x)", color="Orange")
plt.plot (x_data_predict_dot3, y_data_draw_dot3_F, label="f(x)", color="red")
#设置属性
#mpl.rcParams['font.sans-serif'] = ['SimHei']
#mpl.rcParams['axes.unicode_minus'] = False
plt.title("Dot3 拉格朗日插值拟合过程")
plt.legend(loc="upper left")
plt.show()输出结果:
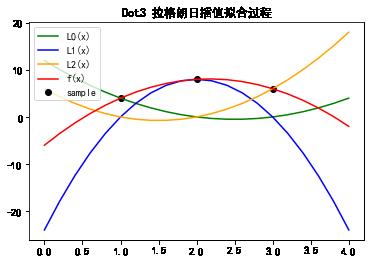
从上述图形可以看出:
- 基函数L0(x) 是一条抛物线,且穿过(x0,y0)点。
- 基函数L1(x) 是一条抛物线,且穿过(x1,y1)点。
- 基函数L2(x) 是一条抛物线,且穿过(x2,y2)点。
- 插值函数F(x) 是L0(x)、L1(x)、L2(x)的线性叠加
- 插值函数F(x)也是一条抛物线,且同时穿过(x0,y0),(x1,y1),(x2,y2)三个采样点。
3.5 拉格朗日插值的优缺点
(1)优点
- 不需要用矩阵求解线性方程组,只需要简单的循环计算就可以得到插值函数。
- 基函数的次数与采样点的个数有对应的关系,N+1点,基函数的次数就是N。
- 插值函数是基函数的简单的线性相加。
(2)缺点
- 当增加一个点或减少一个点时,需要全部重新计算,每个点的个数决定了每个点处的基函数的次数,当采样点的个数发生变化的时候,每个点处的基函数也发生了变化。因此所有的基函数都需要重选计算。
第4章 拉格朗日通用函数的Python实现
4.1 通用的基函数的定义
# 通用的基函数的定义
def LagrangeInterpolationDotN_Li(x, x_data, y_data, k):
size = len(x_data)
i = 0
Ly = y_data[k] # 初值为Yk
while( i < size):
if(i != k):
Ly = Ly * (x-x_data[i])/(x_data[k]-x_data[i])
i += 1
return (Ly)4.2 通用的插值函数的定义
# 通用的插值函数的定义
def LagrangeInterpolationDotN_F(x, x_data, y_data):
size = len(x_data)
k = 0
sum = 0 # 初值为0
while(k < size):
sum = sum + LagrangeInterpolationDotN_Li(x, x_data, y_data, k)
k += 1
return (sum)4.3 拉格朗日2点插值代码示例
(1)采样点
print('两点插值的采样数据:')
x_samples_dot2 = [1, 2]#创建x列表存储数据x值
y_samples_dot2 = [4, 8]#创建y列表存储数据的y值
print("X:", x_samples_dot2)
print("Y:", y_samples_dot2)
plt.scatter(x_samples_dot2, y_samples_dot2, label="sample", color="black")#画点
plt.plot (x_samples_dot2, y_samples_dot2, label="sample", color="red")#画点
mpl.rcParams['font.sans-serif'] = ['SimHei'] #设置中文字体
mpl.rcParams['axes.unicode_minus'] = False
plt.title("LagrangeInterpolation Dot2 采样数据")
plt.legend(loc="upper left")
plt.show()

(2)插值过程
#输入序列x
x_data_predict_dot2 = np.arange(0, 3, 0.2)
#基函数L0预测序列
y_data_predict_dot2_L0 = LagrangeInterpolationDotN_Li(x_data_predict_dot2, x_samples_dot2, y_samples_dot2, 0)
#基函数L1预测序列
y_data_predict_dot2_L1 = LagrangeInterpolationDotN_Li(x_data_predict_dot2, x_samples_dot2, y_samples_dot2, 1)
#插值函数预测序列
y_data_predict_dot2_F = LagrangeInterpolationDotN_F (x_data_predict_dot2, x_samples_dot2, y_samples_dot2)
#显示图形
plt.scatter(x_samples_dot2, y_samples_dot2, label="sample", color="black")#画点
plt.plot (x_data_predict_dot2, y_data_predict_dot2_L0, label="L0(x)", color="green")
plt.plot (x_data_predict_dot2, y_data_predict_dot2_L1, label="L1(x)", color="blue")#画点
plt.plot (x_data_predict_dot2, y_data_predict_dot2_F, label="f(x)", color="red")#画点
#设置属性
mpl.rcParams['font.sans-serif'] = ['SimHei']
mpl.rcParams['axes.unicode_minus'] = False
plt.title("Dot2 拉格朗日插值拟合过程")
plt.legend(loc="upper left")
plt.show()
输出:
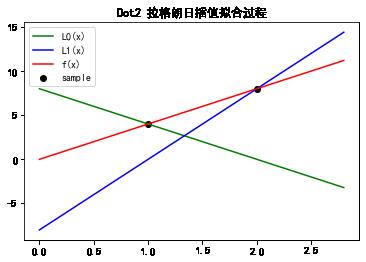
从上述图形可以看出:
- 基函数L0(x) 是一条直线,且穿过(x0,y0)点。
- 基函数L1(x) 是一条直线,且穿过(x1,y1)点。
- 插值函数F(x) 是L0(x)和L1(x)的线性叠加,
- 插值函数F(x) 也是一条直线,且同时穿过(x0,y0)点和(x1,y1)点。
4.4 拉格朗日3点插值代码示例
(1)采样点数据
print('三点插值的采样数据:')
x_samples_dot3 = [1, 2, 3]#创建x列表存储数据x值
y_samples_dot3 = [4, 8, 6]#创建y列表存储数据的y值
print("X:", x_samples_dot3)
print("Y:", y_samples_dot3)
plt.scatter(x_samples_dot3, y_samples_dot3, label="sample", color="black")#画点
plt.plot (x_samples_dot3, y_samples_dot3, label="sample", color="red")#画点
plt.title("Dot3 采样数据")
plt.legend(loc="upper left")
plt.show()
三点插值的采样数据: X: [1, 2, 3] Y: [4, 8, 6]

(2)插值过程
#输入序列x
x_data_predict_dot3 = np.arange(0, 4.2, 0.2)
#基函数L0预测序列
y_data_predict_dot3_L0 = LagrangeInterpolationDotN_Li(x_data_predict_dot3, x_samples_dot3, y_samples_dot3, 0)
#基函数L1预测序列
y_data_predict_dot3_L1 = LagrangeInterpolationDotN_Li(x_data_predict_dot3, x_samples_dot3, y_samples_dot3, 1)
#基函数L2预测序列
y_data_predict_dot3_L2 = LagrangeInterpolationDotN_Li(x_data_predict_dot3, x_samples_dot3, y_samples_dot3, 2)
#基函数L3预测序列
y_data_predict_dot3_F = LagrangeInterpolationDotN_F (x_data_predict_dot3, x_samples_dot3, y_samples_dot3)
#图形显示
plt.scatter(x_samples_dot3, y_samples_dot3, label="sample", color="black")
plt.plot (x_data_predict_dot3, y_data_predict_dot3_L0, label="L0(x)", color="green")
plt.plot (x_data_predict_dot3, y_data_predict_dot3_L1, label="L1(x)", color="blue")
plt.plot (x_data_predict_dot3, y_data_predict_dot3_L2, label="L2(x)", color="Orange")
plt.plot (x_data_predict_dot3, y_data_draw_dot3_F, label="f(x)", color="red")
#设置属性
#mpl.rcParams['font.sans-serif'] = ['SimHei']
#mpl.rcParams['axes.unicode_minus'] = False
plt.title("Dot3 拉格朗日插值拟合过程")
plt.legend(loc="upper left")
plt.show()
从上述图形可以看出:
- 基函数L0(x) 是一条抛物线,且穿过(x0,y0)点。
- 基函数L1(x) 是一条抛物线,且穿过(x1,y1)点。
- 基函数L2(x) 是一条抛物线,且穿过(x2,y2)点。
- 插值函数F(x) 是L0(x)、L1(x)、L2(x)的线性叠加
- 插值函数F(x)也是一条抛物线,且同时穿过(x0,y0),(x1,y1),(x2,y2)三个采样点。
4.5 拉格朗日4点插值代码示例
(1)样本数据
print('四点插值的采样数据:')
x_samples_dot4 = [1, 2, 3, 4]#创建x列表存储数据x值
y_samples_dot4 = [4, 8, 6, 7]#创建y列表存储数据的y值
print("X:", x_samples_dot4)
print("Y:", y_samples_dot4)
plt.scatter(x_samples_dot4, y_samples_dot4, label="sample", color="black")#画点
plt.plot (x_samples_dot4, y_samples_dot4, label="sample", color="red")#画点
plt.title("Dot4 采样数据")
plt.legend(loc="upper left")
plt.show()输出: 四点插值的采样数据: X: [1, 2, 3, 4] Y: [4, 8, 6, 7]

(2)插值过程
#输入序列x
x_data_predict_dot4 = np.arange(0, 5, 0.2)
#基函数L0预测序列
y_data_predict_dot4_L0 = LagrangeInterpolationDotN_Li(x_data_predict_dot4, x_samples_dot4, y_samples_dot4, 0)
#基函数L1预测序列
y_data_predict_dot4_L1 = LagrangeInterpolationDotN_Li(x_data_predict_dot4, x_samples_dot4, y_samples_dot4, 1)
#基函数L2预测序列
y_data_predict_dot4_L2 = LagrangeInterpolationDotN_Li(x_data_predict_dot4, x_samples_dot4, y_samples_dot4, 2)
#基函数L3预测序列
y_data_predict_dot4_L3 = LagrangeInterpolationDotN_Li(x_data_predict_dot4, x_samples_dot4, y_samples_dot4, 3)
#插值函数预测序列
y_data_predict_dot4_F = LagrangeInterpolationDotN_F (x_data_predict_dot4, x_samples_dot4, y_samples_dot4)
#图形显示
plt.scatter(x_samples_dot4, y_samples_dot4, label="sample", color="black")
plt.plot (x_data_predict_dot4, y_data_predict_dot4_L0, label="L0(x)", color="green")
plt.plot (x_data_predict_dot4, y_data_predict_dot4_L1, label="L1(x)", color="blue")
plt.plot (x_data_predict_dot4, y_data_predict_dot4_L2, label="L2(x)", color="Orange")
plt.plot (x_data_predict_dot4, y_data_predict_dot4_L3, label="L3(x)", color="Purple")
plt.plot (x_data_predict_dot4, y_data_predict_dot4_F, label="f(x)", color="red")
#设置属性
mpl.rcParams['font.sans-serif'] = ['SimHei']
mpl.rcParams['axes.unicode_minus'] = False
plt.title("Dot4 拉格朗日插值拟合过程")
plt.legend(loc="upper left")
plt.show()
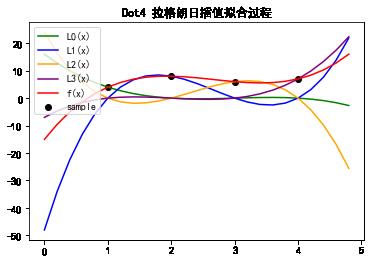
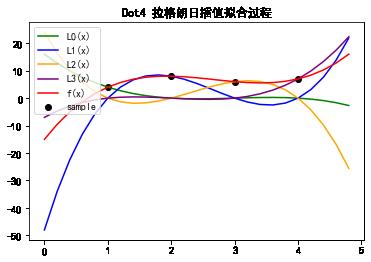
从上述图形可以看出:
- 基函数L0(x) 是一条3次曲线,且穿过(x0,y0)点。
- 基函数L1(x) 是一条3次曲线,且穿过(x1,y1)点。
- 基函数L2(x) 是一条3次曲线,且穿过(x2,y2)点。
- 插值函数F(x) 是L0(x)、L1(x)、L2(x)、L3(x)的线性叠加
- 插值函数F(x)也是一条3次曲线,且同时穿过(x0,y0),(x1,y1),(x2,y2), (x3,y3) 四个采样点。
作者主页(文火冰糖的硅基工坊):https://blog.csdn.net/HiWangWenBing
本文网址:https://blog.csdn.net/HiWangWenBing/article/details/119967939
以上是关于[数值计算-14]:拉格朗日插值与Python代码实现的主要内容,如果未能解决你的问题,请参考以下文章