汽车经销商客户流失预警:逻辑回归(LR)LASSO逐步回归
Posted 大数据部落
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了汽车经销商客户流失预警:逻辑回归(LR)LASSO逐步回归相关的知识,希望对你有一定的参考价值。
全文链接:http://tecdat.cn/?p=32016
原文出处:拓端数据部落公众号
分析师:Shufang Wei
随着社会经济的快速发展和交通基础设施的不断完善,我国汽车市场也得到了迅速增长。 与之配套的汽车售后服务市场成为庞大的黄金市场,发展潜力惊人。 在售后服务市场中,汽车 4S 店以其品牌优势,完整和规范的服务系统以及多种多样的增值服务受到消费者的青睐。但汽车售后市场纷繁复杂, 汽车 4S 店仍 要面对竞争品牌对保有客户的激烈争夺,还有汽车维 修集团、甚至一些小型的汽车维修店对市场的蚕食。 而忠诚度越来越低的客户,也让汽车4S 店感到束手无 策。 因此客户流失预警正成为汽车4S店售后服务领域 的一个重要研究问题。
解决方案
任务/目标
通过客户历史回厂维修车辆信息对客户是否流失进行预警,帮助汽车经销商建立流失预警得分机制,以此对不同得分的客户采取针对性的措施。
数据源准备
此次分析的原始数据分为训练集和测试集,包括客户基础信息数据和客户回厂明细数据, 客户基础信息数据中为客户的个人信息,即客户特征,包含相同的 11个分类特征、 4 个连续特征和 1 个字符特征,共16 个变量。训练集中有 51075 个样本,测试有 10122个样本;客户回厂明细中包括客户在各记录回厂的具体信息,数据共包含从 2011 年到 2018 年 9 月份客户回厂信息。
特征转换
客户年龄和流失率: 可以看出客户随年龄增大,呈现出流失率上升的情况。 为尽量保留连续型变量其独有特征,仅对其做标准化(取对数)处理,降低连续变量量纲的影响。
车价和贷款金额: 都是对于价格的描述,将贷款金额转变为贷款比例,其信息量并无缺失,同时降低了量纲的影响。
分类型变量: 对每一个类别都单独提出作为一个新的虚拟变量。例如:对于“车型 1”,“车型 2”和“缺失”就分为“是否车型 1”,“是否车型 2”和“是否缺失” , 即对一个 N 分类变量划分为 N 个 2 分类变。以上例举的只是部分特征。 最终得到得变量共 56 类,而后根据变量分组样本量和 IV 将变量“车主性质”(BUYERPART)和顾客 ID 给剔除,剩余 54 个变量(53个自变量)。
构造
以上说明了如何抽取相关特征,我们大致有如下训练样本(只列举部分特征)。
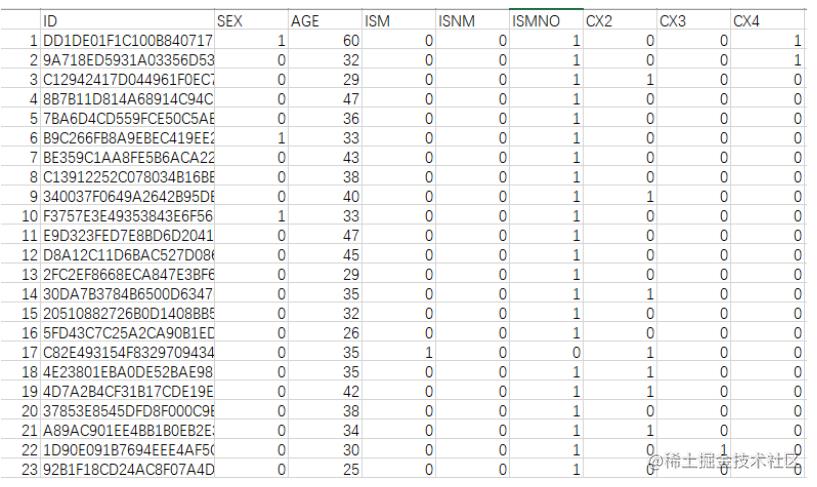
建模
逻辑回归(LR)
逻辑回归是在线性回归的基础上, 套用一个逻辑函数,以估计某种事物的可能性, 可用于解决分类问题。
模型优化
1.上线之前的优化: 变量筛选。
因为变量数目过多, 并且变量之间可能存在多重共线性, 因此在建模之前我们先对变量进行筛选比较在不同变量筛选方法下模型的效果。 在变量筛选过程中尝试以下三种不同的变量筛选方法:
(1)基于模型 AIC 值的向后逐步回归筛选;
(2)基于交叉检验 LASSO 回归的变量筛选;
(3)在 LASSO 变量压缩后再利用基于模型 AIC 值的向后逐步回归筛选。
我们通过比较训练集上的 AUC 值来判别各模型预测能力的强弱。这里的 AUC(Area under the Curve of ROC)是 ROC 曲线下方的面积,是判断二分类预测模型优 劣 的 标 准 之 一 。 ROC ( Receiver Operating Characteristic Curve),称为接收者操作特征曲线,其横坐标为伪阳性率(假正类率),即预测为正而实际非真的概率;纵坐标是真阳性率(真正类率),即预测为真且实际也为真的概率。
AUC 的值越大,说明模型能够牺牲更少的错误预测换取更大的正确预测,模型的预测效果越好。
三种方法训练出来的逻辑回归模型在训练集中的AUC 值比较如下表:
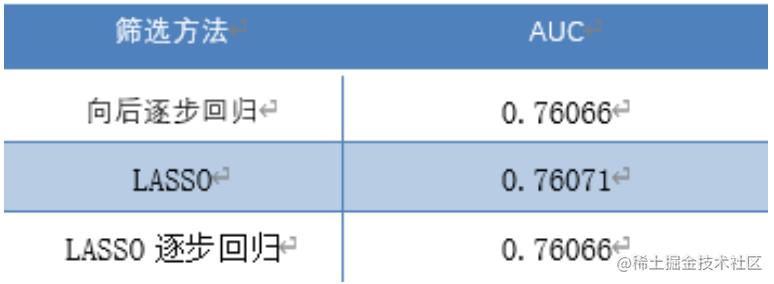
考虑到没有进行 LASSO 变量压缩的模型存在一定的多重共线性,许多变量不显著,而基于 AIC 值的逐步回归筛选方法能够最大让变量通过显著性检验,为了保障模型的泛化能力和解释性,我们选择基于 LASSO和逐步回归的变量筛选方法
项目结果
利用 LASSO 和逐步回归进行变量筛选,以筛选后 的变量进行逻辑回归,得到结果如下表所示。
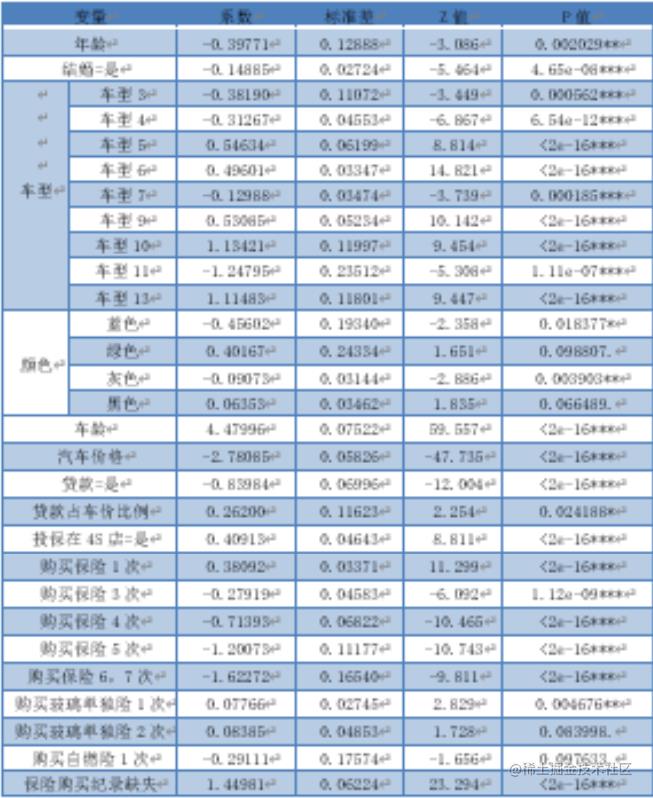
基于以上模型结果我们对 4S 店提出以下建议:
(1) 4S 店应适当关注车价较低的客户,对服务价格等客户比较关心的因素及时做出调整,可利用适当降价等方式吸引低收入客户;
(2)注重首次购买保险的客户,尽可能为客户留下好的印象以加深顾客的体验,计算好损失和收益,可通过免费体验及优惠活动来引起首次购买保险顾客的注意。
得到模型之后, 绘制出流失预测模型在训练集与测试集中的 ROC 曲线如下。 根据 ROC 图中红色曲线与对角线距离最大点处对应的分割作为判别是否流失的概率阈值,计算经过基于LASSO 和逐步回归的变量筛选的逻辑回归模型在训练集和测试上预测结果的混淆矩阵见下表。其中,预测准确率定义为预测结果与实际结果一致的比例,流失客户预测准确率为在所有流失客户中被预测出为流失客户的比例。
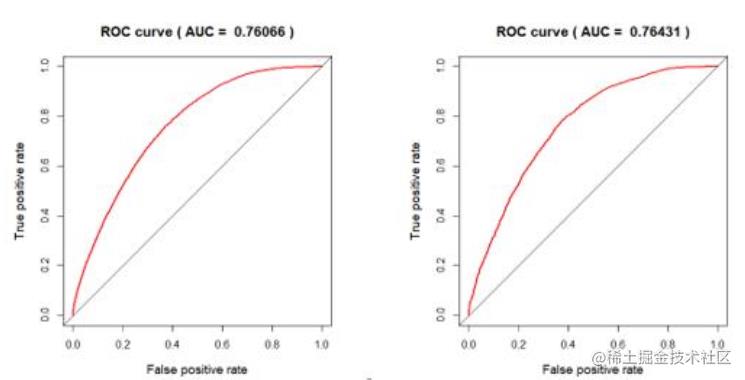
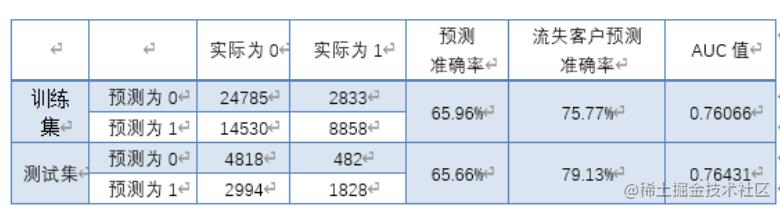
模型总的预测准确率在 65%以上,要优于不用模型识别的情况, 并且可以反映出对客户流失的敏感性。在该模型的指导下, 4S 店的店主会更加珍惜每一位客户,愿意花更多的时间精力去采取挽回措施,从而保障更少的客户流失率。
由于采用一个分割点对客户进行二元分类的方法未能体现出客户流失可能性之间的差异,我们需要对客户流失倾向做进一步的区分。在逻辑回归模型的基础上,我们提出了基于流失胜率(odds)的评分机制设计, 将客户流失得分划分为 1-5 分,以此对不同得分的客户采取针对性的措施。
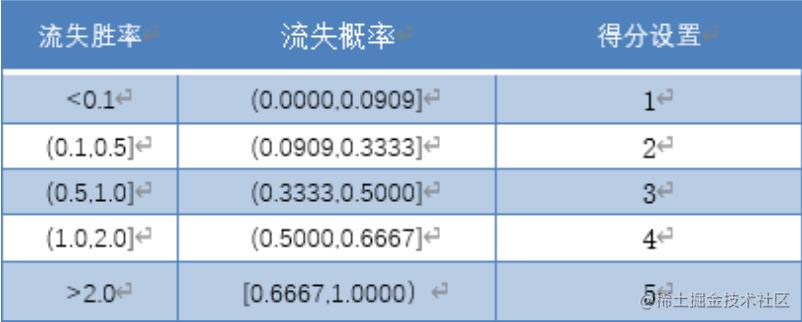
在此机制下的模型预测能力监控报表如下表。
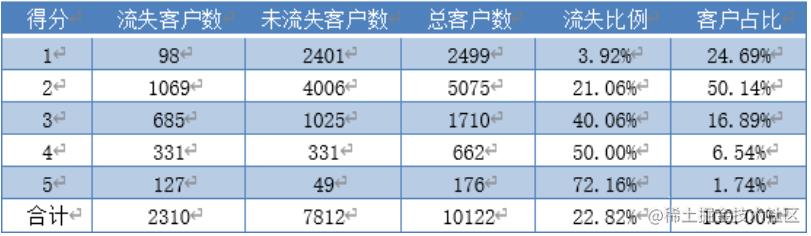
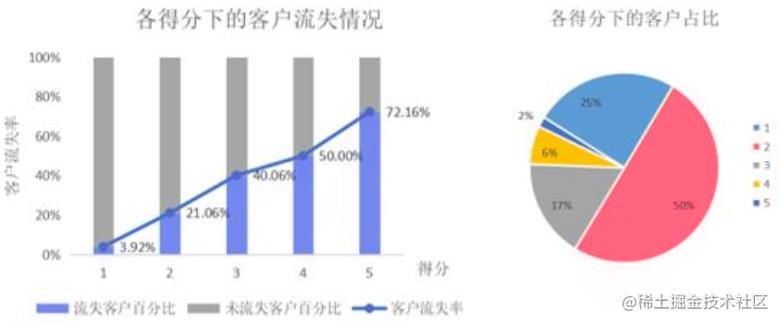
在新的得分机制下,每个得分的流失概率和客户占比较好地得到了预期的要求。根据预警得分, 4S 店的店主应该首先向占比仅 1.74%而流失比例超过 72.16%的得到 5 分预警的客户采取挽回措施,有效减少了挽回成本和对流失倾向很低的客户的打扰。其次, 4S店的店主应该关注占比6.54%的得到4分预警的客户群体,此类客户中有流失比例达到一半,若店主对客户流失现象的回避倾向较高,对 4 分客户群体采取挽回措施仍有不错的针对性。总体而言,新的得分机制设计下,更好地体现了不同预警水平下客户流失倾向的区分度,店主依据此得分报表能够更有针对性地完成流失客户识别和挽回措施的制定,预测模型基本达到了指导售后服务的要求。

关于分析师

在此对Shufang Wei对本文所作的贡献表示诚挚感谢,她在厦门大学完成了统计系专业的硕士学位,专注数据分析、数据挖掘。擅长R语言。
以上是关于汽车经销商客户流失预警:逻辑回归(LR)LASSO逐步回归的主要内容,如果未能解决你的问题,请参考以下文章
传统经销模式难以再续,数商云经销商平台助力汽车服务业强化销售业务管理能力