R语言如何做马尔可夫转换模型markov switching model|附代码数据
Posted 大数据部落
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了R语言如何做马尔可夫转换模型markov switching model|附代码数据相关的知识,希望对你有一定的参考价值。
全文链接:http://tecdat.cn/?p=6962
最近我们被客户要求撰写关于马尔可夫转换模型的研究报告,包括一些图形和统计输出。
假设 有时间序列数据,如下所示。经验表明,目标变量y似乎与解释变量x有关。然而,乍一看,y在水平中间波动,所以它似乎并不总是有稳定的关系(背后有多个状态)
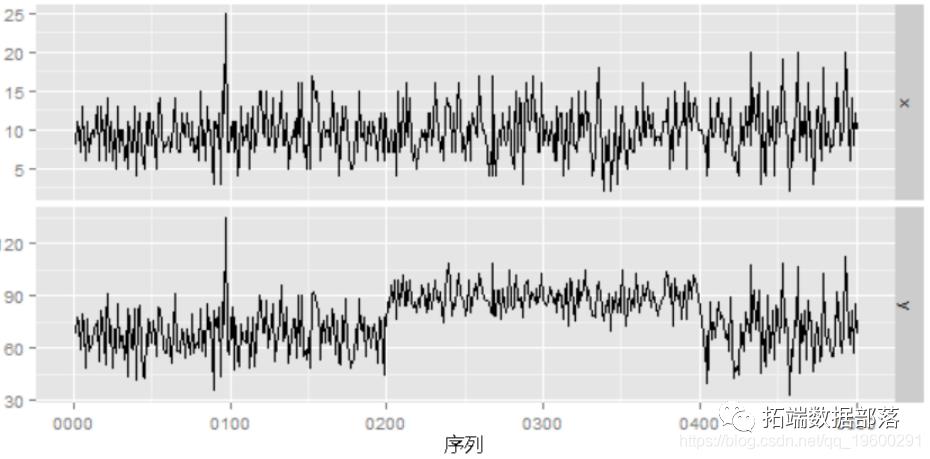
上面的样本数据创建如下。x和y之间的关系数据根据时间改变。
x <- rpois(500, lambda = 10)
y1 <- x * 4 + 20
y2 <- x * 2 + 60
noise <- rnorm(1:500, mean = 10, sd = 5)
y1 <- y1 + noise
y2 <- y2 + noise
y <- c(y1[1:200], y2[201:400], y1[401:500])
observed <- data.frame(x = x, y = y)
x和y1,y2之间的关系如下图所示。
数据
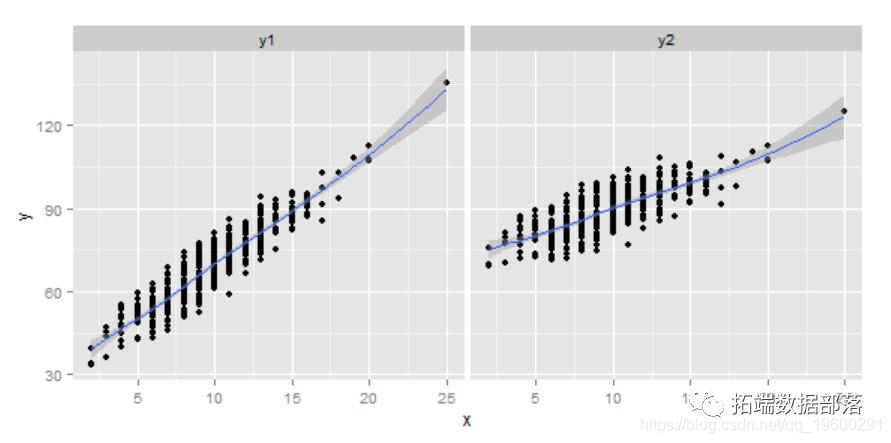
在马尔可夫转换模型中,观察数据被认为是从几个状态生成的,并且如上所示可以很好地分离。
观察到的数据

点击标题查阅往期内容

【视频】马尔可夫链蒙特卡罗方法MCMC原理与R语言实现|数据分享

左右滑动查看更多

01

02

03

04

创建马尔可夫转换模型
模型公式
# Call:
# lm(formula = y ~ x, data = observed)
#
# Residuals:
# Min 1Q Median 3Q Max
# -24.303 -9.354 -1.914 9.617 29.224
#
# Coefficients:
# Estimate Std. Error t value Pr(>|t|)
# (Intercept) 45.7468 1.7202 26.59 <2e-16 ***
# x 3.2262 0.1636 19.71 <2e-16 ***
# ---
# Signif. codes:
# 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
#
# Residual standard error: 11.51 on 498 degrees of freedom
# Multiple R-squared: 0.4383, Adjusted R-squared: 0.4372
# F-statistic: 388.7 on 1 and 498 DF, p-value: < 2.2e-16
参数的含义是
k:马尔可夫转换模型的状态数。在这里,它被指定为后面有两个状态。sw:指定每个参数在状态更改时是否更改p:AR模型系数family:(在GLM的情况下)概率分布族
# 马尔可夫转换模型
#
# AIC BIC logLik
# 3038.846 3101.397 -1513.423
#
# Coefficients:
#
# Regime 1
# ---------
# Estimate Std. Error t value Pr(>|t|)
# (Intercept)(S) 69.3263 4.0606 17.0729 <2e-16 ***
# x(S) 2.1795 0.1187 18.3614 <2e-16 ***
# y_1(S) -0.0103 0.0429 -0.2401 0.8103
# ---
# Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
#
# Residual standard error: 4.99756
# Multiple R-squared: 0.6288
#
# Standardized Residuals:
# Min Q1 Med Q3 Max
# -1.431396e+01 -2.056292e-02 -1.536781e-03 -1.098923e-05 1.584478e+01
#
# Regime 2
# ---------
# Estimate Std. Error t value Pr(>|t|)
# (Intercept)(S) 30.2820 1.7687 17.1210 <2e-16 ***
# x(S) 3.9964 0.0913 43.7722 <2e-16 ***
# y_1(S) -0.0045 0.0203 -0.2217 0.8245
# ---
# Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
#
# Residual standard error: 4.836684
# Multiple R-squared: 0.8663
#
# Standardized Residuals:
# Min Q1 Med Q3 Max
# -13.202056966 -0.771854514 0.002211602 1.162769110 12.417873232
#
# Transition probabilities:
# Regime 1 Regime 2
# Regime 1 0.994973376 0.003347279
# Regime 2 0.005026624 0.996652721
输出中的区制1和区制2表示模型的两个状态 。
# Regime 1
# ---------
# Estimate Std. Error t value Pr(>|t|)
# (Intercept)(S) 69.3263 4.0606 17.0729 <2e-16 ***
# x(S) 2.1795 0.1187 18.3614 <2e-16 ***
# y_1(S) -0.0103 0.0429 -0.2401 0.8103
可以看到区制2 与y1 <- x * 4 + 20匹配。
从调整后的R方值看整体上有所改善。
# Regime 2
# ---------
# Estimate Std. Error t value Pr(>|t|)
# (Intercept)(S) 30.2820 1.7687 17.1210 <2e-16 ***
# x(S) 3.9964 0.0913 43.7722 <2e-16 ***
# y_1(S) -0.0045 0.0203 -0.2217 0.8245
模型
对于每个状态,处于该状态的概率以阴影绘制

每个时间点的概率
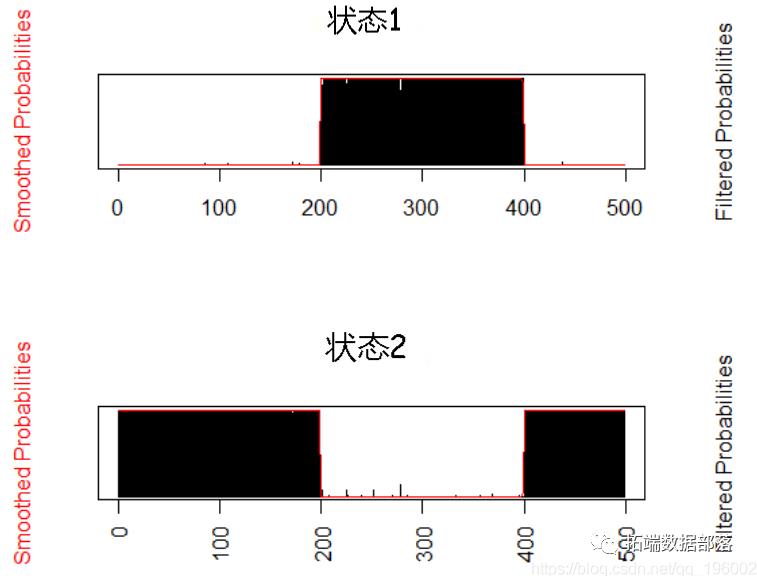
每次获取状态和更改点
如果你想知道你在某个特定时间点所在的regime,那么就选择那个时刻概率最高的 。
> probable
[1] 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2
[30] 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2
...
异常值/变化点是状态更改的时间
c(FALSE, diff(probable) != 0)
[1] FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE
[11] FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE
...
[181] FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE
[191] FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE TRUE
[201] FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE
...
[381] FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE
[391] FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE TRUE
[401] FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE
...
[491] FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE
因此,我们可以看到检测到在第一次数据创建时指定的变化点。

点击文末 “阅读原文”
获取全文完整代码数据资料。
本文选自《R语言如何做马尔可夫转换模型markov switching model》。
点击标题查阅往期内容
matlab用马尔可夫链蒙特卡罗 (MCMC) 的Logistic逻辑回归模型分析汽车实验数据
【视频】马尔可夫链蒙特卡罗方法MCMC原理与R语言实现|数据分享
R语言BUGS/JAGS贝叶斯分析: 马尔科夫链蒙特卡洛方法(MCMC)采样
马尔可夫Markov区制转移模型分析基金利率
马尔可夫区制转移模型Markov regime switching
时变马尔可夫区制转换MRS自回归模型分析经济时间序列
马尔可夫转换模型研究交通伤亡人数事故时间序列预测
如何实现马尔可夫链蒙特卡罗MCMC模型、Metropolis算法?
Matlab用BUGS马尔可夫区制转换Markov switching随机波动率模型、序列蒙特卡罗SMC、M H采样分析时间序列
R语言BUGS序列蒙特卡罗SMC、马尔可夫转换随机波动率SV模型、粒子滤波、Metropolis Hasting采样时间序列分析
matlab用马尔可夫链蒙特卡罗 (MCMC) 的Logistic逻辑回归模型分析汽车实验数据
stata马尔可夫Markov区制转移模型分析基金利率
PYTHON用时变马尔可夫区制转换(MRS)自回归模型分析经济时间序列
R语言使用马尔可夫链对营销中的渠道归因建模
matlab实现MCMC的马尔可夫转换ARMA - GARCH模型估计
R语言隐马尔可夫模型HMM识别不断变化的股票市场条件
R语言中的隐马尔可夫HMM模型实例
用机器学习识别不断变化的股市状况—隐马尔科夫模型(HMM)
Matlab马尔可夫链蒙特卡罗法(MCMC)估计随机波动率(SV,Stochastic Volatility) 模型
MATLAB中的马尔可夫区制转移(Markov regime switching)模型
Matlab马尔可夫区制转换动态回归模型估计GDP增长率
R语言马尔可夫区制转移模型Markov regime switching
stata马尔可夫Markov区制转移模型分析基金利率
R语言如何做马尔可夫转换模型markov switching model
R语言隐马尔可夫模型HMM识别股市变化分析报告
R语言中实现马尔可夫链蒙特卡罗MCMC模型
以上是关于R语言如何做马尔可夫转换模型markov switching model|附代码数据的主要内容,如果未能解决你的问题,请参考以下文章
隐马尔可夫模型(HMM:Hidden Markov Models)
隐马尔可夫模型(Hidden Markov model, HMM)
机器学习算法之——隐马尔可夫模型(Hidden Markov Models,HMM) 代码实现