NLP —— 图模型隐马尔可夫模型（Hidden Markov model，HMM）

Posted 2020-09-20 Determined22

       本文简单整理了以下内容：

      （一）贝叶斯网（Bayesian networks，有向图模型）简单回顾

      （二）隐马尔可夫模型（Hidden Markov model，HMM）

      写着写着还是写成了很规整的样子。以后可能会修改。

 

（一）贝叶斯网简单回顾

      图模型（PGM）根据边是否有向，可以分为有向图模型和无向图模型。

      待补充……

（二）隐马尔可夫模型

      隐马尔可夫模型（Hidden Markov model，HMM）属于生成式模型，被广泛用于序列标注问题，在语音语言领域里比较出名的应用包括语音识别、中文分词（CWS）、词性标注（POS）等等等等。尽管CTC可能是当前更主流的语音识别方案，但这不是本文所关注的，这里只关注这个经典模型本身。

      一、概述

      HMM的概率图模型如下图所示。本文简述的是离散情况下的隐马尔可夫模型（连续情况下的在 [2] 中有讨论，我没细看……）：一条隐藏的马尔可夫链生成的状态随机序列（state sequence，图示的白色节点）$Q=(q_1,q_1,...,q_T)$ 是不可观测的，并记所有可能状态的集合为 $S=\\{S_1,S_2,...,S_N\\}$ ；由它们产生一个可观测的观测随机序列（observation sequence，图示的深色节点）$O=(o_1,o_2,...,o_T)$ ，并记所有可能观测的集合为 $V=\\{v_1,v_2,...,v_M\\}$ 。

      序列的值可以看作是随时刻产生的，每个时刻对应着序列的一个值。所以HMM是个双重随机过程（doubly embedded stochastic process），一个是状态转移，另一个是由状态释放出观测值。在序列标注（Sequence labelling）任务中，模型就是需要对状态序列进行标注。

      根据贝叶斯公式，

$$P(Q|O)=\\frac{P(O,Q)}{P(O)}=\\frac{P(O|Q)P(Q)}{P(O)}$$

对于给定的序列O来说，$P(O)$ 是确定的，所以HMM的任务就是要建模 $P(O,Q)$ 。

      那么问题来了：HMM作为生成式模型，建模联合概率分布，那么关于O、Q的所有可能组合都应该被枚举出来。但实际上，如果序列的元素之间存在长距离依赖，这个任务非常困难。所以才有了下面将会介绍的严格独立性假设。

      观测序列在一个给定时刻下的观测值 $o_t$ 可以看作是特征（特征矢量），而状态序列在那个时刻所对应的状态值 $q_t$ 可以看作是这个特征表示下所对应的类别标号。

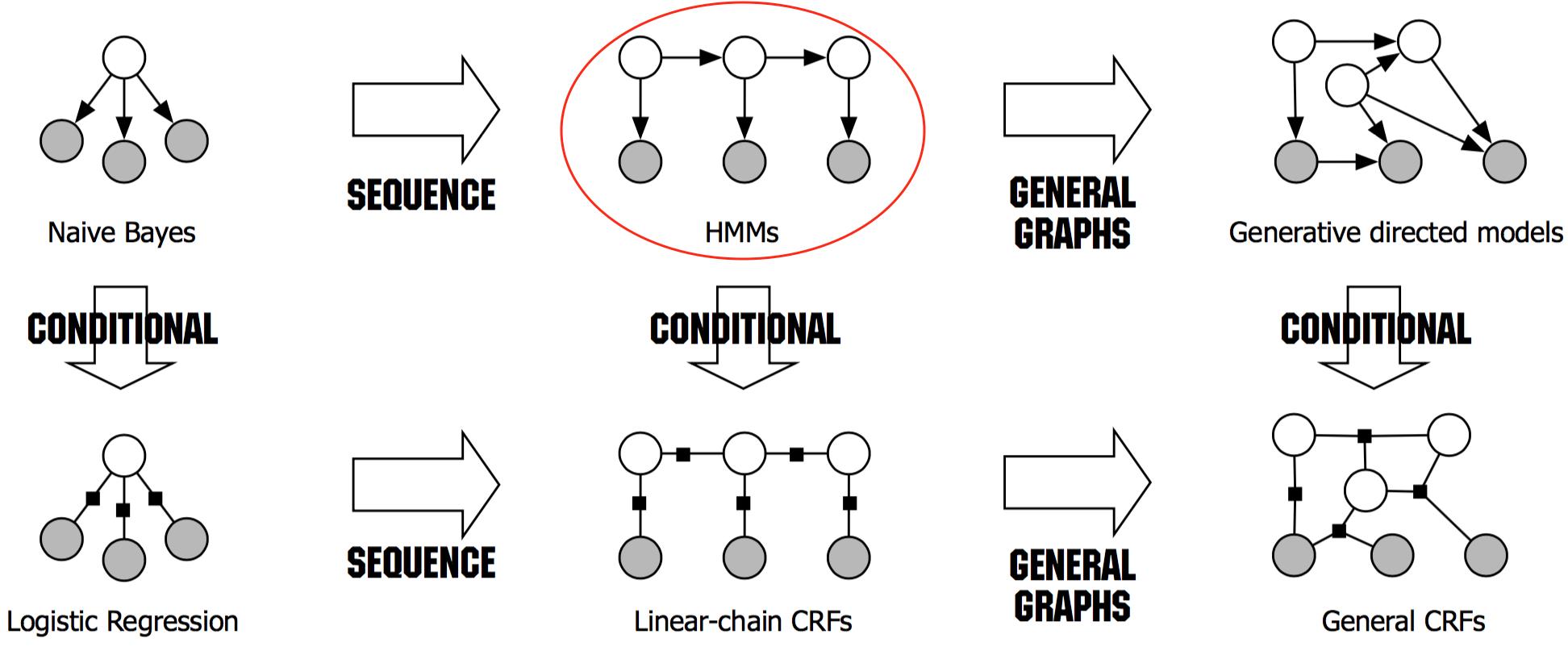
图片来源：[1]

      1. 首先看状态序列（不可观）

      状态序列的值不可观，需要通过观测序列来推断。它由一阶马尔可夫链产生，也就是说每一时刻的状态 $q_t$ 只依赖于前一时刻的状态 $q_{t-1}$ ：

$$P(q_t|q_1,o_1,...,q_{t-1},o_{t-1})=P(q_t|q_{t-1})$$

$$\\begin{aligned}P(q_1,q_2,...,q_t)&=P(q_1)P(q_2|q_1)P(q_3|q_1,q_2)\\cdots P(q_t|q_1,...,q_{t-1})\\\\&=P(q_1)P(q_2|q_1)P(q_3|q_2)\\cdots P(q_t|q_{t-1})\\end{aligned}$$

熟悉贝叶斯网的朋友们都知道，条件独立性可以说是非常核心的一个性质。一阶马尔可夫链的参数是状态转移概率矩阵 $A=[a_{ij}]_{N\\times N}$ 和初始状态概率向量 $\\pi=(\\pi_1,...,\\pi_N)$：

$$a_{ij}=P(q_t=S_j|q_{t-1}=S_i),\\quad \\sum_{j=1}^Na_{ij}=1,\\quad 1\\leq i\\leq N$$

$$\\pi_i=P(q_1=S_i),\\quad \\sum_{i=1}^N\\pi_i=1$$

状态转移。图片来源：[2] 

      2. 接下来看观测序列

      观测序列服从观测独立性假设，也就是说每一时刻的观测值 $o_t$ 只依赖于该时刻的状态值 $q_t$ ：

$$P(o_t|q_1,o_1,...,q_{T},o_{T})=P(o_t|q_t)$$

由此可以引出释放概率矩阵 $B=[b_j(k)]_{N\\times M}$ ：

$$b_j(k)=P(o_t=v_k|q_t=S_j),\\quad \\sum_{k=1}^Mb_j(k)=1,\\quad 1\\leq j\\leq N$$

表示的是在当前时刻状态为 $S_j$ 的条件下观测到到符号为 $v_k$ 的概率。（如果不知道状态 $q_t$ 的具体值 $S_j$ ，那 $b_j(k)$ 的下标 $j$ 就用 $q_t$ 代替；如果不知道观测 $o_t$ 的具体值 $v_k$ ，那 $b_j(k)$ 的 $k$ 就用 $o_t$ 代替。）

      由此，这个模型的参数有三组：初始概率向量 $\\pi$ 、状态转移概率矩阵 $A$ 以及释放概率矩阵 $B$ 。所以可以用 $\\lambda=(\\pi,A,B)$ 来表示一个HMM。

      3. HMM 的数学模型

      HMM 就是要建模 $P(O,Q)$ 。对于给定的一个HMM $\\lambda$ ，下式就是 HMM 模型：

$$\\begin{aligned}P(O,Q|\\lambda)&=\\pi_{q_1}b_{q_1}(o_1)a_{q_1q_2}b_{q_2}(o_2)\\cdots a_{q_{T-1}q_T}b_{q_T}(o_T)\\\\&=\\pi_{q_1}b_{q_1}(o_1)\\prod_{t=2}^Ta_{q_{t-1}q_t}b_{q_t}(o_t)\\end{aligned}$$

这其中，由于不同时刻的释放概率相互独立，所以

$$P(O|Q,\\lambda)=b_{q_1}(o_1)b_{q_2}(o_2)\\cdots b_{q_T}(o_T)$$

根据一阶马尔可夫链，所以

$$P(Q|\\lambda)=\\pi_{q_1}a_{q_1q_2}a_{q_2q_3}\\cdots a_{q_{T-1}q_T}$$

二者结合就得到了上面的式子。

      以词性标注为例

      如果将 $O$ 视作待标注的句子，将 $Q$ 视作标注的词性序列，那么 HMM 各个参数的含义为：转移概率 $a_{ij}$ 表示词性 j 紧跟在词性 i 后的概率，释放概率 $b_j(k)$ 表示词性 j 的条件下会出现词语 k 的概率。

      4. HMM的三个基本问题

      前两个属于inference，第三个属于learning，inference和learning都是概率图模型的基本问题。

      (1). 计算问题（evaluation）：给定一个HMM $\\lambda$ 和一个观测序列 $O$ ，如何高效计算一个观测序列 $O$ 的概率 $P(O|\\lambda)$ ？——前向算法、后向算法

      (2). 解码问题（decoding）：给定一个HMM $\\lambda$ 和一个观测序列 $O$ ，如何最大化 $P(Q|O)$，求出“最有可能”的状态序列 $Q$ ？——维特比算法

      (3). 学习问题（training）：给定若干观测序列 $O$（对应的状态序列 $Q$ 可能已知也可能未知），如何训练出模型参数 $\\lambda$ ，使得 $P(O|\\lambda)$ 最大化？——EM算法

      二、计算问题

      给定一个HMM $\\lambda$ 和一个观测序列 $O$ ，计算一个观测序列 $O$ 的概率 $P(O|\\lambda)$ 可以用直接计算的方式：

$$\\begin{aligned}P(O|\\lambda)&=\\sum_{\\text{all } Q} P(O,Q|\\lambda)\\\\&=\\sum_{\\text{all } Q} P(O|Q,\\lambda)P(Q|\\lambda)\\\\&=\\sum_{\\text{all }q_1,q_2,...,q_T}\\pi_{q_1}b_{q_1}(o_1)a_{q_1q_2}b_{q_2}(o_2)\\cdots a_{q_{T-1}q_T}b_{q_T}(o_T)\\end{aligned}$$

这个式子就是从联合分布求边缘分布，对所有可能的状态序列求和。

      求和号里的每一项都是 $O(2T)$ ，长度为 $T$ 的全部可能的状态序列有 $N^T$ 种，所以这种方式的时间复杂度是 $O(TN^T)$ ，是不可忍受的。

      显然，在这个计算方式下，有大量的重复计算。所以引出了如下两种简化计算方法。

      I、前向算法（forward procedure）

      设到当前时刻 $t$ 的局部观测序列 $o_1,o_2,...,o_t$ ，且当前状态 $q_t$ 是状态集合里的第 $i$ 个状态 $S_i$ ，定义这个概率为前向变量 $\\alpha_t(i)$ ：

$$\\alpha_t(i)=P(o_1,o_2,...,o_t,q_t=S_i|\\lambda)$$

      首先，在初始情况下，显然有

$$\\alpha_1(i)=\\pi_ib_i(o_1),\\quad 1\\leq i\\leq N$$

即需要初始化N个前向变量。

      然后，可以得到下面的归纳方程：

$$\\alpha_{t+1}(j)=\\biggl(\\sum_{i=1}^N\\alpha_t(i)a_{ij}\\biggr)b_j(o_{t+1}),\\quad 1\\leq t\\leq T-1,\\quad 1\\leq j\\leq N$$

这个式子可以用下图来解释

图片来源：[2] 

      情况相当于：想得到在时刻 $t+1$ 时的局部观测序列为 $o_1,o_2,...,o_t,o_{t+1}$ 且状态 $q_{t+1}=S_j$ 的概率 $\\alpha_{t+1}(j)$ ，如何利用此前时刻已经计算过的值？

      仔细想一下，可以从状态转移来入手：现在的情况是，已经给定了状态 $q_{t+1}=S_j$ ，但是转移到它的状态 $q_t$ 可以是任意的。所以，我们可以先求：在时刻 $t$ 时的局部观测序列为 $o_1,o_2,...,o_t$ 且状态 $q_{t+1}=S_j$ 是由状态 $q_t=S_i$ 转移而来的概率，即 $\\alpha_t(i)a_{ij}$ ；由于 $q_t$ 可以是任意的，那么对所有可能（ $S_1,S_2,...,S_N$ ）求和，就得到了在时刻 $t$ 时的局部观测序列为 $o_1,o_2,...,o_t$ 且状态 $q_{t+1}=S_j$ 的概率 $\\sum_{i=1}^N\\alpha_t(i)a_{ij}$ 。那么再乘以 $b_j(o_{t+1})$ ，就得到在时刻 $t+1$ 时的局部观测序列为 $o_1,o_2,...,o_t,o_{t+1}$ 且 状态 $q_{t+1}=S_j$ 的概率 $\\alpha_{t+1}(j)$ 。

      因此，在计算 $\\alpha_{t+1}(j)$ 时，利用了前一时刻 $t$ 的计算结果，这就是计算复杂度得以降低的原因。

      当求得所有前向变量后，就可以按照如下方式计算一个观测序列 $O$ 的概率 $P(O|\\lambda)$ ：

$$\\begin{aligned}P(O|\\lambda)&=P(o_1,o_2,...,o_T|\\lambda)\\\\&=\\sum_{j=1}^NP(o_1,o_2,...,o_T,q_T=S_j|\\lambda)\\\\&=\\sum_{j=1}^N\\alpha_{T}(j)\\end{aligned}$$

      在一个给定的时刻 $t+1$ ，如果给定 $j$ ，那么求取 $\\alpha_{t+1}(j)$ 的时间复杂度为 $O(N)$ ；由于 $j$ 存在N种可能，所以求取在时刻 $t+1$ 的全部 $\\alpha_{t+1}(j)$ 的时间复杂度为 $O(N^2)$ 。又因为有T个时刻，所以时间复杂度为 $O(TN^2)$ ，相比于 $O(TN^T)$ 降低了很多。

      II. 后向算法（backward procedure）

      后向算法需要定义后向变量 $\\beta_t(i)$ ：当前状态 $q_t$ 是状态集合里的第 $i$ 个状态 $S_i$ 的条件下，从时刻 $t+1$ 到 $T$ 的局部观测序列 $o_{t+1},o_{t+2},...,o_T$ 的概率：

$$\\beta_t(i)=P(o_{t+1},o_{t+2},...,o_T|q_t=S_i,\\lambda)$$

      初始情况：$\\beta_T(i)=1,\\quad 1\\leq i\\leq N$

      归纳方程：$\\beta_t(i)=\\sum_{j=1}^Na_{ij}b_j(o_{t+1})\\beta_{t+1}(j),\\quad T-1\\geq t\\geq 1,\\quad 1\\leq i\\leq N$

      终止：$P(O|\\lambda)=\\sum_{i=1}^N\\pi_ib_i(o_1)\\beta_1(i)$

      时间复杂度与前向算法相同。

      前向算法和后向算法有个统一写法：

$$P(O|\\lambda)=\\sum_{i=1}^N\\sum_{j=1}^N\\alpha_t(i)a_{ij}b_j(o_{t+1})\\beta_{t+1}(j),\\quad 1\\leq t\\leq T-1$$

当 $t=1$ 时为前向算法，$t=T-1 $ 时为后向算法。

      III. 一些概率的计算

      利用前向变量和后向变量，可以求解一些情况下某个时刻处在某种状态下的概率。

      1. 给定模型 $\\lambda$ 和一个观测序列 $O$ ，求在时刻 $t$ 时状态 $q_t$ 为 $S_i$ 的概率 $\\gamma_t(i)$ ：根据贝叶斯公式，有

$$\\begin{aligned}\\gamma_t(i)&=P(q_t=S_i|O,\\lambda)\\\\&=\\frac{P(q_t=S_i,O|\\lambda)}{P(O|\\lambda)}\\\\&=\\frac{P(q_t=S_i,O|\\lambda)}{\\sum_{j=1}^NP(q_t=S_j,O|\\lambda)}\\\\&=\\frac{\\alpha_t(i)\\beta_t(i)}{\\sum_{j=1}^N\\alpha_t(j)\\beta_t(j)}\\end{aligned}$$

      显然有 $\\sum_{i=1}^N\\gamma_t(i)=1$ 。

      我们来看一下前向变量和后向变量相乘为什么是 $P(q_t=S_i,O|\\lambda)$ ：为了简单起见，记前向变量等于 P(A, B) ，后向变量等于 P(C|B) ，二者相乘就是 P(B)P(A|B)P(C|B) ，因为 A 和 C 独立所以等于 P(B)P(A, C|B)=P(A, B, C) 。

      2. 给定模型 $\\lambda$ 和一个观测序列 $O$ ，求在时刻 $t$ 时状态 $q_t$ 为 $S_i$ 且在下一时刻 $t+1$ 的状态 $q_{t+1}$ 为 $S_j$ 的概率：

$$\\begin{aligned}\\xi_t(i,j)&=P(q_t=S_i,q_{t+1}=S_j|O,\\lambda)\\\\&=\\frac{P(q_t=S_i,q_{t+1}=S_j,O|\\lambda)}{P(O|\\lambda)}\\\\&=\\frac{P(q_t=S_i,q_{t+1}=S_j,O|\\lambda)}{\\sum_{i=1}^N\\sum_{j=1}^NP(q_t=S_j,q_{t+1}=S_j,O|\\lambda)}\\\\&=\\frac{\\alpha_t(i)a_{ij}b_j(o_{t+1})\\beta_{t+1}(j)}{\\sum_{i=1}^N\\sum_{j=1}^N\\alpha_t(i)a_{ij}b_j(o_{t+1})\\beta_{t+1}(j)}\\end{aligned}$$

图片来源：[2]

      3. 这两个值的关系

$$\\gamma_t(i)=\\sum_{j=1}^N\\xi_t(i,j)$$

      三、解码问题

      给定一个HMM $\\lambda$ 和一个观测序列 $O$ ，如何最大化 $P(Q|O)$，求出“最有可能”的状态序列 $Q$ ？

      换句话说，怎样可以快速地从 $N^T$ 个序列里找到概率最大的那一个：

$$\\begin{aligned}\\max_{q_1,q_2,...,q_T}P(q_1,q_2,...,q_T|O,\\lambda)&=\\max_{q_1,q_2,...,q_T}\\frac{P(q_1,q_2,...,q_T,O|\\lambda)}{P(O|\\lambda)}\\\\&=\\max_{q_1,q_2,...,q_T}{P(q_1,q_2,...,q_T,O|\\lambda)} \\end{aligned}$$

      I. 近似算法

      很直观的思路是：在每个时刻 $t$ 都选择当前时刻下概率最大的状态 $q_t^*$ ，进而组成状态序列，尽管这个状态序列并不能保证整体上是概率最大的。

      在时刻 $t$ 时最可能的状态在状态集合 $S$ 中的序号是 $i=\\arg\\max_{1\\leq i\\leq N}\\gamma_t(i)$ ，进而 $q_t^*=S_i$ 。

      此外，这种方法还有个问题就是，不能保证两个相邻时刻的状态间存在转移概率。也就是说，这种方法所得到的状态序列可能根本就不是个合法序列。

      II. 维特比算法（Viterbi algorithm）

      维特比算法是一种动态规划方法。动态规划的基础是贝尔曼最优性原理（Bellman\'s Principle of Optimality）：多级决策过程的最优策略有如下性质——不论初始状态和初始决策如何，其余的决策对于初始决策所形成的状态来说，必定也是一个最优策略。

      在解码问题里就是说：如果最优状态序列 $q_1^*,q_2^*,...,q_{T}^*$ 在时刻 $t$ 的状态 $q_t^*$ 已知为 $S_i$ ，那么从 $q_t^*$ 到 $q_T^*$ 的局部状态序列一定是所有可能的状态序列里最优的。通俗一点说，已知最优路径 P ，那么我们在路径上选择一个节点，从起点到该节点的这段局部路径P1一定是所有可能的局部路径里最优的；同样地，从这个节点到终点的局部路径P2一定是所有可能的局部路径里最优的。既然有了这个性质，且看维特比算法是如何求解出最优状态序列的：

      维特比算法就是利用以下的方法求解最优序列：从起始时刻 $t=1$开始，递推地找出在时刻 $t$ 的状态为 $S_i$ 的各个可能的状态序列中的最大概率，一直求解到时刻 $t=T$ 的状态为 $S_i$ 的最大概率，并得到时刻 $T$ 的状态 $S_j$ ；然后向前回溯求得其他时刻的状态。

      定义如下维特比变量 $\\delta_t(i)$ ：能够输出已知的观测序列 $o_1,...,o_t$ 、且在时刻 $t$ 的状态 $q_t$ 为 $S_i$ 的所有局部状态序列 $q_1,q_2,...,q_{t-1},S_i$ 中，概率最大的序列 $q_1^*,q_2^*,...,q_{t-1}^*,S_i$ 所对应的概率值为

$$\\delta_t(i)=\\max_{q_1,q_2,...,q_{t-1}}P(q_1,q_2,...,q_{t-1},q_t=S_i,o_1,...,o_t|\\lambda)$$

      首先，初始情况下，有

$$\\delta_1(i)=\\pi_ib_i(o_1),\\quad 1\\leq i\\leq N$$

$$\\psi_1(i)=S_0$$

第二个式子在下面马上介绍。

      然后，可以得到递归关系

$$\\delta_{t}(i)=\\biggl(\\max_{1\\leq j\\leq N}[\\delta_{t-1}(j)a_{ji}]\\biggl)b_i(o_{t}),\\quad 2\\leq t\\leq T,\\quad 1\\leq i\\leq N$$

$$\\psi_t(i)=\\arg\\max_{S_j,1\\leq j\\leq N}[\\delta_{t-1}(j)a_{ji}], \\quad 2\\leq t\\leq T,\\quad 1\\leq i\\leq N$$

这个递归关系和前向算法很类似：现在已知时刻 $t$ 的状态 $q_t$ 为 $S_i$ ，需要求解 $\\delta_{t}(i)$ ，如何利用已经求解过的（即时刻 $t$ 之前的）值。同前向算法一样，依然是从状态转移入手：时刻 $t-1$ 的状态 $S_j$ 并不是任取的（ $1\\leq j\\leq N$ ），对于 $\\delta_{t}(i)$ 所对应的最优局部状态序列 $q_1^*,q_2^*,...,q_{t-1}^*,S_i$ 来说，它是唯一的。那么，为了得到 $\\delta_{t}(i)$ ，就需要确定出 $S_j$ ，也就是 $S_i$ 由谁转移而来。也就是说，需要全部的 $\\delta_{t-1}(j)$（ $1\\leq j\\leq N$ ），然后找出 $\\delta_{t-1}(j)a_{ji}b_i(o_{t})$ 最大的一个。由 $S_i$ 释放出 $o_t$（观测序列的每个值都是已知的）的概率 $b_i(o_{t})$ 为固定值，所以无需考虑，就得到了上面的递推式。$\\psi_t(i)$ 是记录前一时刻状态的数组：对于在时刻 $t$ 的状态 $q_t$ 为 $S_i$ 的概率最大的局部状态序列 $q_1^*,q_2^*,...,q_{t-1}^*,S_i$ ，记录其在时刻 $t-1$ 的状态 $q_{t-1}^*$ 的状态值 $S_j$ 。有了这个信息，就可以不断向前回溯。

      那么可以得到最终时刻的状态：只有计算到最终时刻 $T$ 的 $\\delta_T(i)$ ，才知道最优序列 $q_1^*,...,q_T^*$ 的概率（此前的概率不管多大，因为没有转移到最后一个状态，所以都是局部的）以及其在最终时刻的状态 $q_T^*$ ，才能进一步回溯求解此前每个时刻的状态

$$i=\\arg\\max_{1\\leq i\\leq N}\\delta_T(i)$$

$$q_T^*=S_i$$

      最后需要回溯，得到每个时刻的状态

$$q_{t}^*=\\psi_{t+1}(q_{t+1}^*),\\quad T-1\\geq t \\geq 1$$

      维特比算法的时间复杂度和前向算法、后向算法相同，为 $O(TN^2)$ 。

      如果我上面说的还是抽象、不够清楚，可以看看 [3] 的例题10.3，把整个过程跟着走一遍，很快就懂了。

      在具体实现过程中，为避免多个很小的数相乘导致浮点数下溢，所以可以取对数使相乘变为相加。

      四、学习问题

      此前两个问题，计算问题和解码问题，都是在已知模型参数 $\\lambda$ 和观测序列 $O$ 的情况下，去推断状态序列 $Q$ 。

      现在的问题是，已知若干个长度相同的观测序列和对应的状态序列 $\\{(Q_1,O_1),(Q_2,O_2),...\\}$（对应的状态序列也可能未知），如何训练模型参数。

      I. 监督学习

      在有标注数据（对应的状态序列已知）的情况下，可以使用极大似然估计。此时，给定一个观测序列 $O$ 和对应的状态序列 $Q$ ，模型参数有以下的频数估计的形式：

$$\\begin{aligned}\\overline\\pi_i&=frequency\\text{ in state }S_i\\text{ at time }1\\\\&=\\delta(q_1,S_i)\\end{aligned}$$

$$\\begin{aligned}\\overline a_{ij}&=\\frac{\\text{#}transitions\\text{ from state }S_i\\text{ to state }S_j}{\\text{#}transitions\\text{ from state }S_i}\\\\&=\\frac{\\sum_{t=1}^{T-1}\\delta(q_t,S_i)\\delta(q_{t+1},S_j)}{\\sum_{t=1}^{T-1}\\delta(q_t,S_i)}\\end{aligned}$$

$$\\begin{aligned}\\overline b_{j}(k)&=\\frac{frequency\\text{ in state }S_j\\text{ and observing symbol }v_k}{frequency\\text{ in state }S_j}\\\\&=\\frac{\\sum_{t=1}^{T}\\delta(q_t,S_j)\\delta(o_{t},v_k)}{\\sum_{t=1}^{T}\\delta(q_t,S_j)}\\end{aligned}$$

式中的 $\\delta(\\cdot,\\cdot)$ 是克罗内克函数（Kronecker），$\\delta(x,y)=1\\text{ if }x=y\\text{ else }0$ 。跟示性函数 $I(\\cdot)$ 有点像，示性函数是括号内的条件为真则1，为假则0。

      II. 无监督学习

      无监督学习HMM模型参数的motivation是状态序列的获取是有很大代价的，所以在这种情况下需要根据观测序列直接训练模型。

      状态序列 $Q$ 作为隐变量的情况下，可以用EM算法来训练HMM。基本思路是，首先将模型参数随机初始化为 $\\lambda^{(0)}=(\\pi^{(0)},A^{(0)},B^{(0)})$（需要满足各自的限制条件，就是三个求和式），然后在模型 $\\lambda_0$ 下得到该模型下的隐变量的期望值，将上面有监督学习的全部频数都替换为期望频数。

      用于HMM训练的EM算法被称为Baum-Welch算法（前向-后向算法），模型参数有以下的更新式：

$$\\overline\\pi_i^{(n+1)}=P(q_1=S_i|O,\\lambda)=\\gamma_1(i)$$

$$\\overline a_{ij}^{(n+1)}=\\frac{\\sum_{t=1}^{T-1}\\xi_t(i,j)}{\\sum_{t=1}^{T-1}\\gamma_t(i)}$$

$$\\overline b_{j}^{(n+1)}=\\frac{\\sum_{t=1}^{T}\\gamma_t(j)\\delta(o_t,v_k)}{\\sum_{t=1}^{T}\\gamma_t(j)}$$

这个式子是迭代更新的：因为等式右端的式子是在模型 $\\lambda^{(n)}=(\\pi^{(n)},A^{(n)},B^{(n)})$ 下计算出的，进而得到新一次迭代的参数值，如此不断迭代更新。

      推导并不复杂，[3] 写的很详细。需要注意的是， [3] 的式(10.33)写成 $Q(\\lambda,\\overline\\lambda)=\\sum_QP(O,Q|\\overline\\lambda)\\log P(O,Q|\\lambda)$ 比较合适，原来的写法有歧义。之前写过博客简单梳理了一下EM算法。

      关于何时停机：用下面的对数运算的方式来判断某个参数是否已经收敛

$$|\\log P(O|\\lambda^{(n+1)})-\\log P(O|\\lambda^{(n)})|<\\epsilon$$

由于EM算法中存在求和操作（Viterbi算法只有乘积操作），所以不能简单地使用取对数来避免浮点数下溢，采用的方式是设置一个比例系数，将概率值乘以它来放大；当每次迭代结束后，再把比例系数取消掉，继续下一次迭代。

 

 

 

 

参考：

[1] An Introduction to Conditional Random Fields for Relational Learning

[2] A Tutorial on Hidden Markov Models and Selected Applications in Speech Recognition

[3] 《统计学习方法》

[4] 《统计自然语言处理》

[5] 漫谈Hidden Markov Model 

[6] 52NLP的关于HMM的系列文章

[7] 知乎：基于CTC等端到端语音识别方法的出现是否标志着统治数年的HMM方法终结？