统计学中频数分布表怎么做

Posted 2023-05-15

演示机型：华为MateBookX系统版本：win10APP版本：SPSS20.0PC中文版

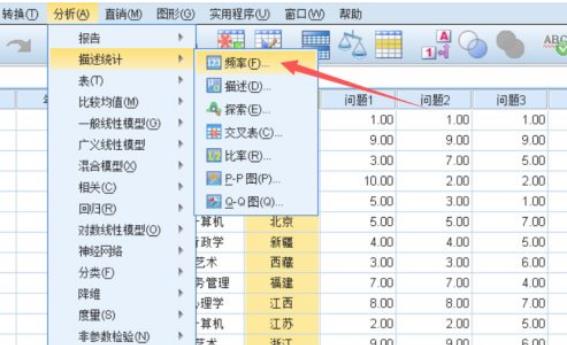
1、点击菜单栏分析——描述统计——频率，弹出对话框。

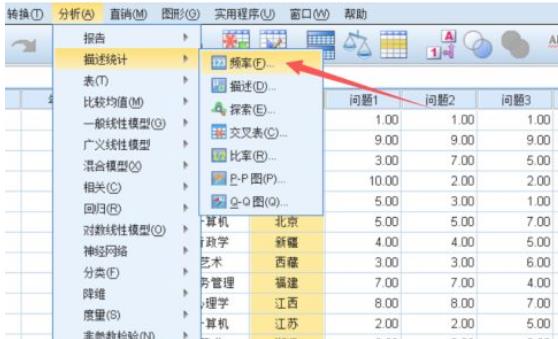
2、把左侧需要进行频数统计的变量移动右侧框中，还可以根据需要设置统计量、格式等，点击确定。

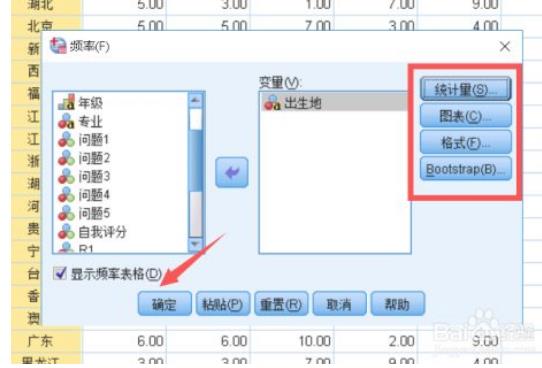
3、可以看到局限性，只适用于分组数据，而不适用于连续型数据。针对连续型数据，就需要用到分组频数分布表。

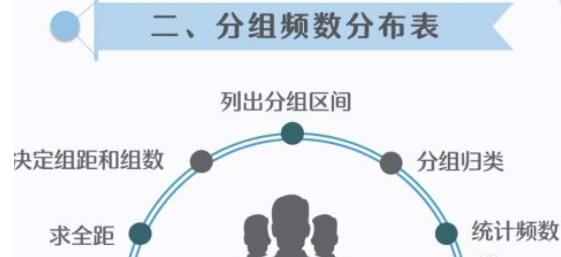
4、分组频数分布表的流程步骤：计算全距、决定组距和组数、列出区间、分组归类、频数统计。

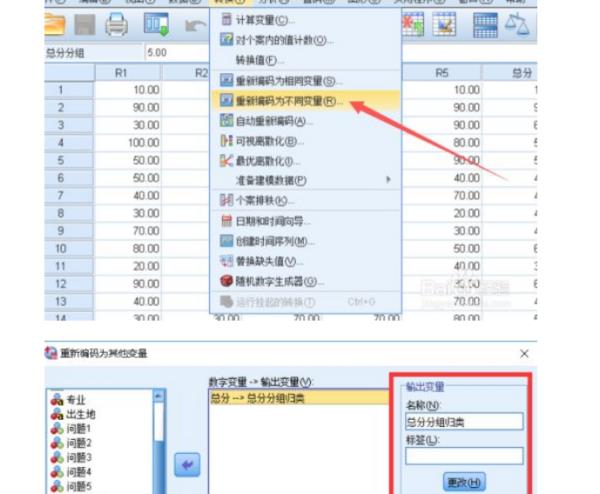
5、利用SPSS进行分组归类，点击转换--重新编码为不同变量，在输出变量处起个名字，点击旧值新值，按图中设置范围区间里的值对应新的值，并添加，后面全部点击确定即可生成一列新的变量。

6、利用SPSS统计分组后的频数，点击菜单分析--描述统计--频率，步骤和简单频数分析是一样的（只是多了一步将连续型数据进行分组的步骤）。

参考技术A

演示机型：华为MateBookX系统版本：win10APP版本：SPSS20.0PC中文版
1、点击菜单栏分析——描述统计——频率，弹出对话框。

2、把左侧需要进行频数统计的变量移动右侧框中，还可以根据需要设置统计量、格式等，点击确定。

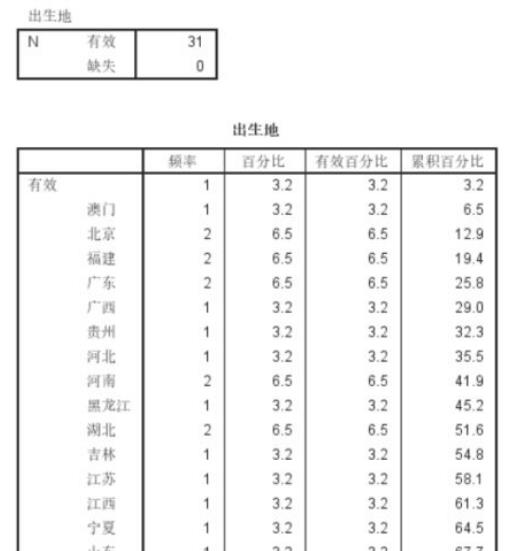
3、可以看到局限性，只适用于分组数据，而不适用于连续型数据。针对连续型数据，就需要用到分组频数分布表。

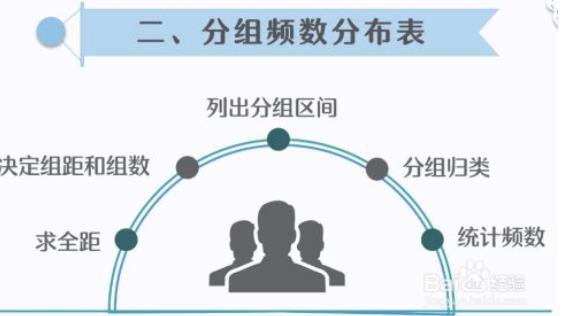
4、分组频数分布表的流程步骤：计算全距、决定组距和组数、列出区间、分组归类、频数统计。

5、利用SPSS进行分组归类，点击转换--重新编码为不同变量，在输出变量处起个名字，点击旧值新值，按图中设置范围区间里的值对应新的值，并添加，后面全部点击确定即可生成一列新的变量。

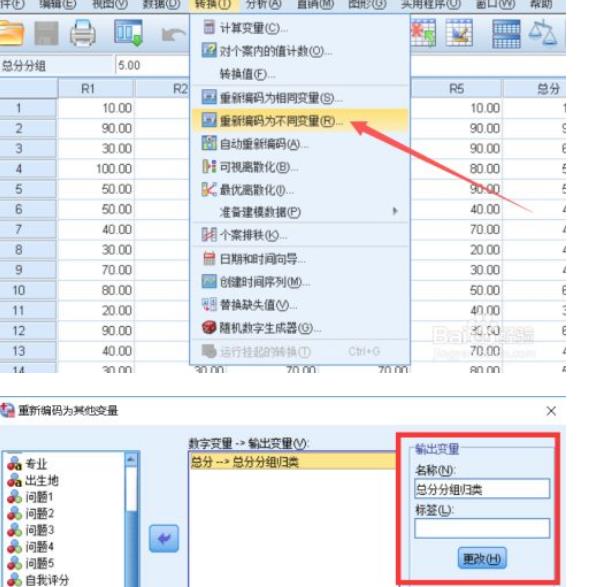
6、利用SPSS统计分组后的频数，点击菜单分析--描述统计--频率，步骤和简单频数分析是一样的（只是多了一步将连续型数据进行分组的步骤）。

数据的描述性统计

数据的集中趋势

众数

众数是样本观测值在频数分布表中频数最多的那一组的组中值，主要应用于大面积普查研究之中。

众数是在一组数据中,出现次数最多的数据，是一组数据中的原数据，而不是相应的次数。

一组数据中的众数不止一个，如数据2、3、-1、2、1、3中，2、3都出现了两次，它们都是这组数据中的众数。

一般来说，一组数据中，出现次数最多的数就叫这组数据的众数。

例如：

1，2，3，3，4的众数是3。
但是，如果有两个或两个以上个数出现次数都是最多的，那么这几个数都是这组数据的众数。

1，2，2，3，3，4的众数是2和3。
还有，如果所有数据出现的次数都一样，那么这组数据没有众数。

1，2，3，4，5没有众数。

计算方法：

 

分位数

分位数（Quantile），亦称分位点，是指将一个随机变量的概率分布范围分为几个等份的数值点，常用的有中位数（即二分位数）、四分位数、百分位数等。

?分位数指的就是连续分布函数中的一个点，这个点对应概率p。若概率0<p<1，随机变量X或它的概率分布的分位数Za，是指满足条件p(X≤Za)=α的实数

常见分类

二分位数

对于有限的数集，可以通过把所有观察值高低排序后找出正中间的一个作为中位数。如果观察值有偶数个，则中位数不唯一，通常取最中间的两个数值的平均数作为中位数，即二分位数。

一个数集中最多有一半的数值小于中位数，也最多有一半的数值大于中位数。如果大于和小于中位数的数值个数均少于一半，那么数集中必有若干值等同于中位数。

计算有限个数的数据的二分位数的方法是：把所有的同类数据按照大小的顺序排列。如果数据的个数是奇数，则中间那个数据就是这群数据的中位数；如果数据的个数是偶数，则中间那2个数据的算术平均值就是这群数据的中位数。

四分位数

第一四分位数(Q1)，又称“较小四分位数”，等于该样本中所有数值由小到大排列后第25%的数字；

第二四分位数(Q2)，又称“中位数”，等于该样本中所有数值由小到大排列后第50%的数字；

第三四分位数(Q3)，又称“较大四分位数”，等于该样本中所有数值由小到大排列后第75%的数字。

第三四分位数与第一四分位数的差距又称四分位距。

中位数

中位数（又称中值，英语：Median），统计学中的专有名词，代表一个样本、种群或概率分布中的一个数值，其可将数值集合划分为相等的上下两部分。 对于有限的数集，可以通过把所有观察值高低排序后找出正中间的一个作为中位数。如果观察值有偶数个，通常取最中间的两个数值的平均数作为中位数。

中位数，又称中点数，中值。中位数是按顺序排列的一组数据中居于中间位置的数，即在这组数据中，有一半的数据比他大，有一半的数据比他小，这里用 M0.5来表示中位数。（注意：中位数和众数不同，众数指最多的数，众数有时不止一个，而中位数只能有一个。）

 

对于一组有限个数的数据来说，它们的中位数是这样的一种数：这群数据里的一半的数据比它大，而另外一半数据比它小。 计算有限个数的数据的中位数的方法是：把所有的同类数据按照大小的顺序排列。如果数据的个数是奇数，则中间那个数据就是这群数据的中位数；如果数据的个数是偶数，则中间那2个数据的算术平均值就是这群数据的中位数。 中位数：也就是选取中间的数，是一种衡量集中趋势的方法。

计算示例：

 

平均数

平均数，统计学术语，是表示一组数据集中趋势的量数，是指在一组数据中所有数据之和再除以这组数据的个数。它是反映数据集中趋势的一项指标。解答平均数应用题的关键在于确定“总数量”以及和总数量对应的总份数。 在统计工作中，平均数（均值）和标准差是描述数据资料集中趋势和离散程度的两个最重要的测度值。

统计平均数是用于反映现象总体的一般水平，或分布的集中趋势。数值平均数是总体标志总量对比总体单位数而计算的。 平均数是统计中的一个重要概念。小学数学里所讲的平均数一般是指算术平均数，也就是一组数据的和除以这组数据的个数所得的商。在统计中算术平均数常用于表示统计对象的一般水平，它是描述数据集中位置的一个统计量。既可以用它来反映一组数据的一般情况、和平均水平，也可以用它进行不同组数据的比较，以看出组与组之间的差别。 用平均数表示一组数据的情况，有直观、简明的特点，所以在日常生活中经常用到，如平均速度、平均身高、平均产量、平均成绩等等。

算术平均数

加权平均数

几何平均数

例题如下：

3头牛和6只羊一天共吃草93千克，6头牛和5只羊一天共吃草130千克。3头牛一天共吃草多少千克？ 
正解：
45千克 直接求法：利用公式求出平均数，这是由“均分”思想产生的方法。 
总数量÷总份数=平均数 基数求法：利用公式求平均数。
这里是选设各数中最小者为基数，它是由“补差”思想产生的方法。 
基数+各数与基数的差÷总份数=平均数

李师傅前4天平均每天加工30个零件，改进技术后，第五天加工零件55个，李师傅5天中平均每天加工多少零件？ 
解答：
先算出5天的总零件数：30×4+55=175（个）
再求出5天中平均每天加零件的个数。 （30×4+55）÷5=35（个）

四（1）班有学生40人，数学期末考试时有三位同学困病缺考，平均成绩是80分。
后来这三位同学补考，成绩分别为88分、87分和85分，这时全班同学的平均成绩是多少分？ 
正解：
（40—3）×80=2960（分） （2960+88+87+85）÷40=80.5（分）

王师傅4天平均加工26个零件，第5天加工的零件数比5天平均数还多4.8个。王师傅第5天加工多少个零件？ 
解答：
设王师傅第5天加工，x个零件。
由5天平均数这个“量”可列方程。 
X－4.8=26×4+x）÷5 
5x－24=104+x 
4x=128 
X=32

一个学生前六次测验的平均分是93分，比七次测验的平均分高3分，他第七次测验得了多少分？ 
正解：
93×6=558（分） 
93—3=90（分） 
90×7=630（分） 
630—588=72（分）

小明前几次数学测验的平均成绩是84分，这一次要考100分才能把平均成绩提高到86分。这一次是第几次测验？ 
解答：
（100－84）÷（86－84）=8次

小松前几次考试的平均成绩是84分，这一次考了94分就把平均成绩提高到86分了。这一次是第几次考试？ 
正解：
（94—84） ÷（86—84）=10÷2=5（次）

张明前五次数学测验的平均成绩是88分。为了使平均成绩达到92.5分，张明要连续考多少次满分？（每次测验满分是100分。） 
解答：
（92.5－88）×5÷（100－92.5）=4.5×5÷7.5=3（次）

小王前5次数学考试的平均成绩是85.8分，为了使平均成绩尽快达到90分以上，小王至少还要参加几次考试？（每次满分为100分。） 
正解：
（90—85.8）×5÷(100-90)=4.2×5÷10=2.1

 

相对离散程度

离散系数

离散系数又称变异系数，是统计学当中的常用统计指标。离散系数是测度数据离散程度的相对统计 量，主要是用于比较不同样本数据的离散程度。离散系数大，说明数据的离散程度也大；离散系数小，说明数据的离散程度也小。

在概率论和统计学

 

离散系数（coefficient of variation）只在平均值不为零时有定义，而且一般适用于平均值大于零的情况。变异系数也被称为标准离差率或单位风险。

离散系数反映单位均值上的离散程度，常用在两个总体均值不等的离散程度的比较上。若两个总体的均值相等，则比较标准差系数与比较标准差是等价的。一组数据的标准差与其相应的均值之比，是测度数据离散程度的相对指标，其作用主要是用于比较不同组别数据的离散程度。 其计算公式为 

 

 ( σ：标准差，μ：平均值)。在对比情况下，离散系数较大的其分布情况差异也大。

数据的离中趋势

数值型数据

方差

 

方差是指一组数据中的各个数减这组数据的平均数的平方和的平均数。 如（1,2,3,4,5）这组数据的方差； 先求出这组数据的平均数（1+2+3+4+5）÷5＝3； 然后再求各个数与平均数的差的平方和，(1-3)2+(2-3)2+(3-3)2+(4-3)2+(5-3)2＝10; 再求平均数10÷5＝2，即这组数据的方差为2.

极差

极差又称范围误差或全距(Range)，以R表示，是用来表示统计资料中的变异量数(measures of variation)，其最大值与最小值之间的差距，即最大值减最小值后所得之数据。 它是标志值变动的最大范围，它是测定标志变动的最简单的指标。移动极差（Moving Range）是其中的一种。极差不能用作比较，单位不同 ，方差能用作比较， 因为都是个比率。

计算公式

计算示例：求下列数字集的极差 65、81、73、85、94、79、67、83、82 解：极差指的是这些数字分开得有多远，计算方法是：用其中最大的数减去最小的数。 首先找其中最大的数，65、81、73、85、94、79、67、83、82 最大数是94，94比其他数都大，所以它是这些数字中最大的。然后要减去这些数字中最小的。该数字集中最小的数字是65。 那么极差是： 94−65=29 这个数字越大，表示分得越开，最大数和最小数之间的差就越大，该数越小，数字间就越紧密，这就是极差的概念。

标准差?

标准差（Standard Deviation） ，中文环境中又常称均方差，是离均差平方的算术平均数的平方根，用σ表示。标准差是方差的算术平方根。标准差能反映一个数据集的离散程度。平均数相同的两组数据，标准差未必相同。

计算示例

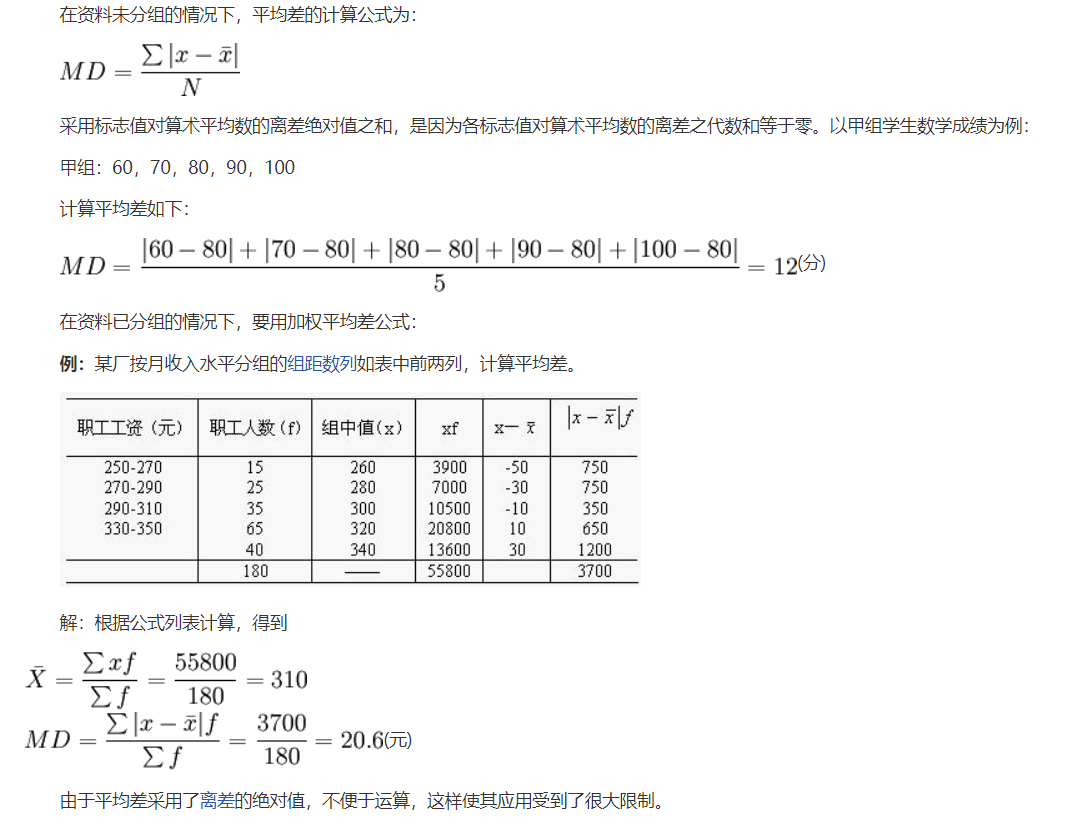
平均差

平均差是总体各单位标志对其算术平均数的离差绝对值的算术平均数。它综合反映了总体各单位标志值的变动程度。平均差越大，则表示标志变动度越大，反之则表示标志变动度越小。

平均差的计算

 

顺序数据

四分位差

四分位差又称内距、也称四分间距(inter-quartile range)，是指将各个变量值按大小顺序排列，然后将此数列分成四等份，所得第三个四分位上的值与第一个四分位上的值的差。

四分位差反映了中间50%数据的离散程度。其数值越小，说明中间的数据越集中；数值越大，说明中间的数据越分散。与极差(最大值与最小值之差)相比，四分位差不受极值的影响。此外，由于中位数处于数据的中间位置，因此四分位差的大小在一定程度上也说明了中位数对一组数据的代表程度。

计算示例

 

 

分类数据

异众比率

异众比率又称离异比率或变差比，是指的是非众数的次数与全部变量值总次数的比率，即众数不能代表的那一部分变量值在总体中的比重。

异众比率的作用是衡量众数对一组数据的代表程度。异众比率越大，说明非众数组的频数占总频数的比重越大，众数的代表性就越差；异众比率越小，说明非众数组的频数占总频数的比重越小，众数的代表性越好。

 

分布形状

偏态系数

偏度是统计数据分布偏斜方向和程度的度量，是统计数据分布非对称程度的数字特征。

计算公式

三种情况

 

峰态系数

是指次数分布曲线顶峰的尖平程度，是次数分布的又一重要特征。统计上，常以正态分布曲线为标准，来观察比较某一次数分布曲线的顶端正党风尖顶或平顶以及尖平程度的大小。

根据变量值的集中与分散程度，峰度一般可表现为三种形态：尖顶峰度、平顶峰度和标准峰度。当变量值的次数在众数周围分布比较集中，使次数分布曲线比正态分布曲线顶峰更为隆起尖峭，称为尖顶峰度；当变量值的次数在众数周围分布较为分散，使次数分布曲线较正态分布曲线更为平缓，称为平顶峰度。可见，尖顶峰度或平顶峰度都是相对正态分布曲线的标准峰度而言的。

峰态的测定，一般是采用统计动差方法，即以四阶中心动差V4为测定依据，将V4除以其标准差的四次方σ4，以消除单位量纲的影响，便于不同次数分布曲线的峰度比较，从而得到以无名数表示的相对数，即为峰度的测定值（β）。

计算公式为：

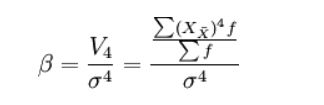
由统计计算分析可知，当次数分布为正态分布曲线时，β = 3，以此为标准就可比较分析各种次数分布曲线的峰度。当β > 3时，表示分布曲线呈尖顶峰度，为尖顶曲线，说明变量值的次数较为密集地分布在众数的周围，β值越大于3，分布曲线的顶端越尖峭。当β < 3时，表示分布曲线呈平顶峰度，为平顶曲线，说明变量值的次数分布比较均匀地分散在众数的两侧，β值越小于3，则分布曲线的顶峰就越平缓。一般当β值接近于1.8时，分布曲线呈水平矩形分布形态，说明各组变量值的次数相同。当β值小于1.8时，次数分布曲线趋向“U”型分布。实际统计分析中，通常将偏度和峰度结合起来运用，以判断变量分布是否接近于正态分布。