关于用matlab仿真一级倒立摆的LQY控制的程序，大伙谁有帮忙提供一下，多谢了

Posted 2023-05-12

模型已经建好了，PID和LQR的程序已经编好了，就差LQY的程序了，用到的参数有M 小车质量1.096Kg
m 摆杆质量 0.109Kg
b 小车摩擦系数 0.1N/m/sec
l 摆杆转动轴心到杆质心的长度 0.25m
如果谁能给我提供LRY的程序，我会把自己编写的PID和LQR的程序送给他，多谢了！

参考技术A 这是这个研究领域的高难度的问题,说不定还处于保密阶段
.你就想这么简单把人家的秘密拿走啊.
劝你还是自己写吧.

基于滑模变结构的倒立摆控制系统matlab仿真

目录

一、理论基础

二、核心程序

三、测试结果

---

一、理论基础

       随着关于倒立摆控制系统研究的不断推进，倒立摆在设计结构上有很多种类，其中最常见的有直线型倒立摆和环形倒立摆（如图1.1所示），从倒立摆的阶数方面看，可以分为3阶倒立摆，4阶倒立摆甚至更高阶倒立摆等。倒立摆在使用过程中，往往通过一个小车在水平方向上来回行驶，使得小车上方的倒立摆达到一个稳定的状态。而在为了达到这个动态平衡状态，研究者需要尝试不同的控制技术使得倒立摆达到一个严格的稳定状态。

     倒立摆在实际作业过程中，其动态平衡往往是一个非线性的变化过程，因为采用传统的控制方式将无法满足倒立摆达到动态平衡的需求。针对这个问题，有学者提出了一种基于滑膜变结构的控制算法。滑膜变结构控制系统是一种非线性的控制方法，其对于控制对象的系统参数以及外部的干扰影响因素具有较强的不变性，即无论设置不同控制系统参数还是设置不同环境干扰因素，其均可保证控制过程的稳定性。

       倒立摆控制系统总体的动能和势能分别可以表示为：

 

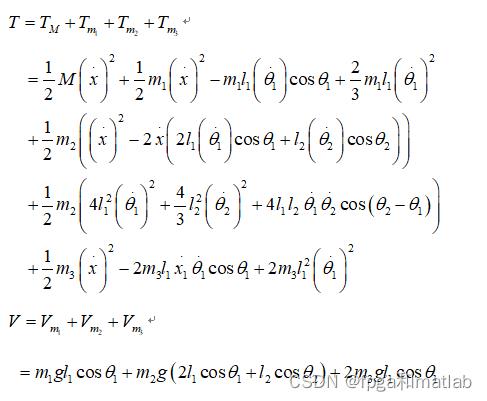
二、核心程序

...............................................
 

LEN= 10000;
%离散
ts = 0.01;
g=9.81;
m1=0.04;
m2=0.132;
m3=0.208;
l1=0.09;
l2=0.27;

K12 = 3*(-2*g*m1-4*g*m2-4*g*m3)/(2*(-4*m1-3*m2-12*m3)*l1);
K13 = 9*m2*g/(2*(-4*m1-3*m2-12*m3)*l1);

K17 = 3*(-2*m1-m2-4*m3)/(2*(-4*m1-3*m2-12*m3)*l1);

K22 = 2*g*(m1+2*(m2+m3))/(4*m2*l2-16/9*(m1+(3*m2+m3))*l2);
K23 = 4*g*(m1+3*(m2+m3))/3/(4*m2*l2-16/9*(m1+(3*m2+m3))*l2);
K27 = (2*(m1+2*(m2+m3))-4/3*(m1+3*(m2+m3)))/(4*m2*l2-16/9*(m1+(3*m2+m3))*l2);



A  = [0,0 ,0 ,1,0,0;
      0,0,0,0,1,0;
      0,0,0,0,0,1;
      0,0,0,0,0,0;
      0,K12,K13,0,0,0;
      0,K22,K23,0,0,0;];
  
B   = [0;
       0;
       0;
       1;
       K17;
       K27];  
 C  = [0.4495,4.1930,-8.8675,0.8035,0.0151,-1.5196]; 
[F,G]   = c2d(A,B,ts);
Q       = diag([1 0 1 1 0 1]);
R       = [1];
[K,p,e] = dlqr(F,G,Q,R);
F       = F-G*K;  

%初始条件
x1_0 = 1;
x2_0 = 0;
x3_0 = 0;
x4_0 = 1;
x5_0 = 0;
x6_0 = 0;
u_0  = 0;

for k=1:1:LEN
    k
    time(k) = k*ts;
    x1(k)   = F(1,1)*x1_0+F(1,2)*x2_0+F(1,3)*x3_0+F(1,4)*x4_0+F(1,5)*x5_0+F(1,6)*x6_0+G(1)*u_0;
    x2(k)   = F(2,1)*x1_0+F(2,2)*x2_0+F(2,3)*x3_0+F(2,4)*x4_0+F(2,5)*x5_0+F(2,6)*x6_0+G(2)*u_0;
    x3(k)   = F(3,1)*x1_0+F(3,2)*x2_0+F(3,3)*x3_0+F(3,4)*x4_0+F(3,5)*x5_0+F(3,6)*x6_0+G(3)*u_0;
    x4(k)   = F(4,1)*x1_0+F(4,2)*x2_0+F(4,3)*x3_0+F(4,4)*x4_0+F(4,5)*x5_0+F(4,6)*x6_0+G(4)*u_0;
    x5(k)   = F(5,1)*x1_0+F(5,2)*x2_0+F(5,3)*x3_0+F(5,4)*x4_0+F(5,5)*x5_0+F(5,6)*x6_0+G(5)*u_0;
    x6(k)   = F(6,1)*x1_0+F(6,2)*x2_0+F(6,3)*x3_0+F(6,4)*x4_0+F(6,5)*x5_0+F(6,6)*x6_0+G(6)*u_0;
    u       =-K(1)*x1(k)-K(2)*x2(k)-K(3)*x3(k)-K(4)*x4(k)-K(5)*x5(k)-K(6)*x6(k);
    %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
    X_back(k)= u+randn/50;
    c    = 1e-4;
    if k==1
       X_back2=0;
    else
       X_back2=X_back(k)-X_back(k-1);
    end
    s    = c*X_back2;
    y    =-inv(C*B)*(C*A*s+5*s+0.05*sign(s));
    %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
    X(k)    = min(y);
    u_0     = X(k);
    x1_0    = x1(k);
    x2_0    = x2(k);
    x3_0    = x3(k);
    x4_0    = x4(k);
    x5_0    = x5(k);    
    x6_0    = x6(k);    
end
x1a=x1;
x2a=x2;
x3a=x3;
x4a=x4;
x5a=x5;
x6a=x6;
A  = [0,0 ,0 ,1,0,0;
      0,0,0,0,1,0;
      0,0,0,0,0,1;
      0,0,0,0,0,0;
      0,K12,K13,0,0,0;
      0,K22,K23,0,0,0;];
  
B   = [0;
       0;
       0;
       1;
       K17;
       K27];  
 C  = [0.4495,4.1930,-8.8675,0.8035,0.0151,-1.5196]; 
[F,G]   = c2d(A,B,ts);
Q       = diag([1 0 1 1 0 1]);
R       = [1];
[K,p,e] = dlqr(F,G,Q,R);
F       = F-G*K;  

%初始条件
x1_0 = 1;
x2_0 = 0;
x3_0 = 0;
x4_0 = 1;
x5_0 = 0;
x6_0 = 0;
u_0  = 0;

for k=1:1:LEN
    k
    time(k) = k*ts;
    x1(k)   = F(1,1)*x1_0+F(1,2)*x2_0+F(1,3)*x3_0+F(1,4)*x4_0+F(1,5)*x5_0+F(1,6)*x6_0+G(1)*u_0;
    x2(k)   = F(2,1)*x1_0+F(2,2)*x2_0+F(2,3)*x3_0+F(2,4)*x4_0+F(2,5)*x5_0+F(2,6)*x6_0+G(2)*u_0;
    x3(k)   = F(3,1)*x1_0+F(3,2)*x2_0+F(3,3)*x3_0+F(3,4)*x4_0+F(3,5)*x5_0+F(3,6)*x6_0+G(3)*u_0;
    x4(k)   = F(4,1)*x1_0+F(4,2)*x2_0+F(4,3)*x3_0+F(4,4)*x4_0+F(4,5)*x5_0+F(4,6)*x6_0+G(4)*u_0;
    x5(k)   = F(5,1)*x1_0+F(5,2)*x2_0+F(5,3)*x3_0+F(5,4)*x4_0+F(5,5)*x5_0+F(5,6)*x6_0+G(5)*u_0;
    x6(k)   = F(6,1)*x1_0+F(6,2)*x2_0+F(6,3)*x3_0+F(6,4)*x4_0+F(6,5)*x5_0+F(6,6)*x6_0+G(6)*u_0;
    u       =-K(1)*x1(k)-K(2)*x2(k)-K(3)*x3(k)-K(4)*x4(k)-K(5)*x5(k)-K(6)*x6(k);
    %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
    X_back(k)= u+randn/50;
    c    = 1e-4;
    if k==1
       X_back2=0;
    else
       X_back2=X_back(k)-X_back(k-1);
    end
    s    = c*X_back2;
    y    =-inv(C*B)*(C*A*s+5*s+0.05*sats(s));
    %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
    X(k)    = min(y);
    u_0     = X(k);
    x1_0    = x1(k);
    x2_0    = x2(k);
    x3_0    = x3(k);
    x4_0    = x4(k);
    x5_0    = x5(k);    
    x6_0    = x6(k);    
end
x1b=x1;
x2b=x2;
x3b=x3;
x4b=x4;
x5b=x5;
x6b=x6;

.............................................

三、测试结果

	参数名称	参数数值与单位
1	重力加速度g	9.81m/s2
2	杆1的质量m1	0.04kg
3	杆2的质量m2	0.132kg
4	质量块的质量m3	0.208kg
5	摆杆1转动轴心到杆质心的长度l1	0.09m
6	摆杆2转动轴心到杆质心的长度l2	0.27m
7	采样时间T	0.02s

通过上述参数，得到如下的仿真结果：

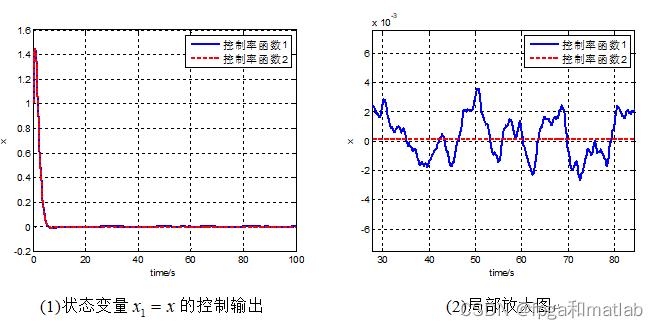
采用第二种控制律函数不仅可以达到相应的控制效果，而且可以有效降低控制系统的抖振。

 

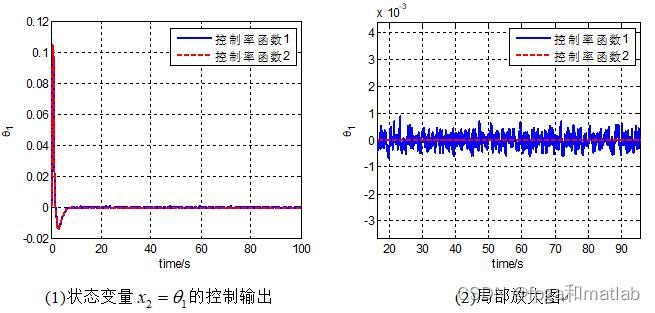
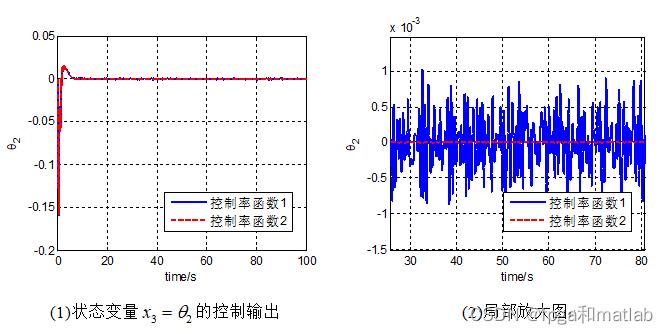
 A08-82