）

Posted 2023-01-31 最爱吃兽奶710

第十一章

11.1 确定执行的优先级

垃圾邮件分类器算法： 为了解决这样一个问题，我们首先要做的决定是如何选择并表达特征向量 $x$ 。我们可以选择一个由 $100$ 个最常出现在垃圾邮件中的词所构成的列表，根据这些词是否有在邮件中出现，来获得我们的特征向量（出现为 $1$，不出现为 $0$），尺寸为 $100\times 1$ 。

为了构建这个分类器算法，我们可以做很多事，例如：

• 收集更多的数据，让我们有更多的垃圾邮件和非垃圾邮件的样本
• 基于邮件的路由信息开发一系列复杂的特征
• 基于邮件的正文信息开发一系列复杂的特征，包括考虑截词的处理
• 为探测刻意的拼写错误（把watch写成w4tch）开发复杂的算法

在上面这些选项中，非常难决定应该在哪一项上花费时间和精力，作出明智的选择，比随着感觉走要更好。

11.2 误差分析

帮助解决在各种提升性能的方法中进行选择。

1. 推荐方法
   • 从一个简单的能快速实现的算法开始，实现该算法并用交叉验证集数据测试这个算法
   • 绘制学习曲线，决定是增加更多数据，或者添加更多特征，还是其他选择
   • 进行误差分析：人工检查交叉验证集中我们算法中产生预测误差的样本，看看这些样本是否有某种系统化的趋势
2. 用一个数字去直观的体现算法性能是重要的
3. 误差分析应该在验证集上进行

11.3 不对称性分类的误差评估

不对称性分类： 数据集中一种类别的数量比另一种多得多，如：癌症影像识别。

如果有一个偏斜类分类任务（癌症诊断），用分类精确度并不能很好地衡量算法性能，如癌症诊断任务中可能现有数据集中仅有 $5\%$ 的样本为阳性样本，因此即使我们用一个只会输出负类的分类器，也可以获得 $95\%$ 的准确率，但显然这是没有意义的。为解决上述问题，引入下述评价指标。

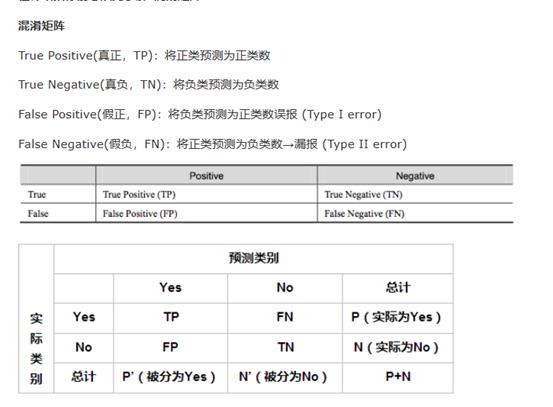
我们将算法预测的结果分为四种情况：

• 正确肯定（True Positive,TP）： 预测为真，实际为真
• 正确否定（True Negative,TN）： 预测为假，实际为假
• 错误肯定（False Positive,FP）： 预测为真，实际为假
• 错误否定（False Negative,FN）： 预测为假，实际为真

查准率： Precision = TP / (TP + FP)
例，在所有我们预测有恶性肿瘤的病人中，实际上有恶性肿瘤的病人的百分比，越高越好。

查全率： Recall = TP / (TP + FN)
例，在所有实际上有恶性肿瘤的病人中，成功预测有恶性肿瘤的病人的百分比，越高越好。

11.4 查准率和查全率的权衡

如果我们希望只在非常确信的情况下预测为真（肿瘤为恶性），即我们希望更高的查准率，我们可以使用比0.5更大的阀值，如0.7，0.9。这样做我们会减少错误预测病人为恶性肿瘤的情况，同时却会增加未能成功预测肿瘤为恶性的情况。

如果我们希望提高查全率，尽可能地让所有有可能是恶性肿瘤的病人都得到进一步地检查、诊断，我们可以使用比0.5更小的阀值，如0.3。

我们可以将不同阀值情况下，查全率与查准率的关系绘制成图表，曲线的形状根据数据的不同而不同：

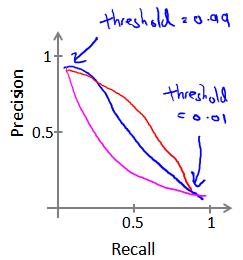
我们希望有一个帮助我们选择这个阀值的方法。一种方法是计算F1值（F1 Score），其计算公式为：$F1Score=\frac{2PR}{P+R}$

我们选择使得F1值最高的阀值。

11.5 机器学习数据

“不是谁有最好的算法就能获胜。而是谁拥有最多的数据”。

海量数据是合理的。

1. 假设特征 $x\in R^{n+1}$ 已经提供了足够的信息，可以去准确的预测出标签 $y$。判断这一点：给出这样的特征输入 $x$，人类专家是否可以给出正确的输出。
2. 学习算法可以使用更多的参数
3. 使用更多的训练数据，不易过拟合。

第十二章

12.1 优化目标

逻辑回归：

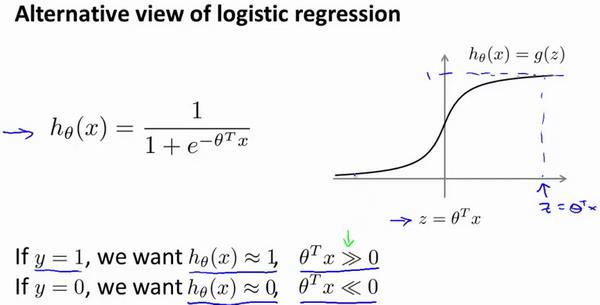
$Cost(h_{\theta }(x),y)=-y\log h_{\theta }(x)-(1-y)\log (1-h_{\theta }(x))$

令 $cos{t}_1({\theta }^{T}x)=-\log h_{\theta }(x)$，$cos{t}_0({\theta }^{T}x)=-\log (1-h_{\theta }(x))$

SVM hypothesis：

$\underset{\theta }{\min }C\sum _{i=1}^m[y^{(i)}cos{t}_1({\theta }^T{x}^{(i)})+(1-y^{(i)})cos{t}_0({\theta }^T{x}^{(i)})]+\frac{1}{2}\sum _{i=1}^n{\theta }_j^2$

Hypothesis：

$h_{\theta }(x)=\begin{array}{ll}1& if{\theta }^{T}x\ge 0\\ 0& otherwise\end{array}$

12.2 直观上对大间隔的理解

SVM：

决策边界：

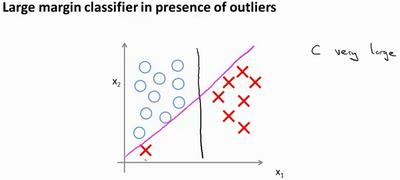
如果你将C设置的不要太大，则你最终会得到这条黑线；当不是非常非常大的时候，它可以忽略掉一些异常点的影响，得到更好的决策边界。

• $C$ 较大时，相当于 $\lambda$ 较小，可能会导致过拟合，高方差
• $C$ 较小时，相当于 $\lambda$ 较大，可能会导致欠拟合，高偏差

12.3 核函数1

使用高级数的多项式模型来解决无法用直线进行分隔的分类问题：

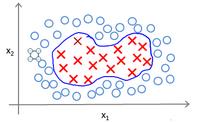
为了获得上图所示的判定边界，我们的模型可能是 ${\theta }_0+{\theta }_1{x}_1+{\theta }_2{x}_2+{\theta }_3{x}_1{x}_2+{\theta }_4{x}_1^2+{\theta }_5{x}_2^2+...$ 的形式。

我们可以用一系列的新的特征 $f$ 来替换模型中的每一项： $f_1=x_1,f_2=x_2,f_3=x_1{x}_2,f_4=x_1^2$