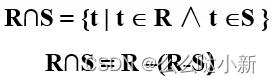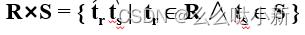关系数据库

Posted 2023-01-24 么么哒小新

文章目录

• 2.1关系数据结构及形式化定义
• • 2.1.1 关系
  • • 1.域：
    • 2.笛卡儿积：
    • 3.关系：
    • • 关系可以有三种类型：
      • 基本关系具有的性质
  • 2.1.2 关系模式
  • • 定义：
    • 关系模式与关系
• 2.2 关系操作
• • 2.2.1 基本的关系操作
  • • 关系操作的特点
  • 2.2.2 关系数据语言的种类
• 2.3 关系的完整性
• • 2.3.1 实体完整性
  • 2.3.2 参照完整性
  • 2.3.3 用户定义的完整性
• 2.4 关系代数
• • 2.4.1 传统的集合运算
  • 2.4.2 专门的关系运算
  • • 1.选择
    • 2.投影
    • 3.连接
    • • 等值连接
      • 自然连接
    • 4.除
    • 一些练习

2.1关系数据结构及形式化定义

2.1.1 关系

1.域：

是一组具有相同数据类型的值的集合。

2.笛卡儿积：

给定一组域D1、D2、…、Dn，这些域中可以有相同的。 D1、D2、…、Dn的笛卡尔积为：
​ D1×D2×…×Dn =（d1,d2,…,dn）|di∈Di, i=1,2,…,n其中每一个元素（ d1,d2,…,dn ）叫作一个n元组或简称元组元素中的每一个值di叫作一个分量。

• D1×D2×…×Dn基数M为：M=
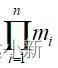
• 笛卡尔积可表示为一个二维表。表中的每行对应一个元组，表中的每列对应一个域。

3.关系：

D1×D2×…×Dn 的子集叫做在域 D1，D2，…，Dn上的关系(Relation) ，表示为：
​ R(D1, D2 …, Dn)
R是关系名，n为关系的目。

• 关系是笛卡尔积的有限子集，所以关系也是一个二维表。

• 若关系中的某一个或多个属性的集合能唯一地标识一个元组，则称该属性或属性组为超码。

• 如果构成超码属性组的任意真子集都不能成为超码，这样的最小超码称为候选码。

• 若一个关系有多个候选码，则选定其中一个为主码。候选码的诸属性称为主属性。

• 不包含在任何候选码中的属性称为非主属性或非码属性。

关系可以有三种类型：

• 基本关系（基本表或基表）
  • 实际存在的表，是实际存储数据的逻辑表示。
• 查询表
  • 查询结果对应的表。
• 视图表
  • 由基本表或其他视图表导出的表，是虚表，不对应实际存储的数据。

基本关系具有的性质

1. 列是同质的，每一列中的分量是同一类型的数据，来自同一个域。
2. 不同的列可出自同一个域，其中的每一列称为一个属性，不同的属性要给予不同的属性名。
3. 列的顺序无所谓，列的次序可以任意交换。
4. 任意两个元组的候选码不能相同。
5. 行的顺序无所谓，行的次序可以任意交换。
6. 分量必须取原子值，每一个分量都必须是不可分的数据项。

2.1.2 关系模式

• 关系模式是对关系的描述。
• 关系是元组的集合，因此关系模式必须指出这个元组集合的结构，即它由哪些属性构成，这些属性来自哪些域，以及属性与域之间的映象关系。
• 现实世界的许多已有事实限定了关系模式所有可能的关系必须满足一定的完整性约束。
• 这些约束或者通过对属性取值范围的限定，或者通过属性值间的相互关连反映出来。关系模式应当刻划出这些完整性约束条件。
• 因此一个关系模式应当是一个5元组。

定义：

关系的描述称为关系模式。它可以形式化地表示为：
R(U，D，dom，F)
其中R为关系名，U为组成该关系的属性名集合，D为属性组U中属性所来自的域，dom为属性向域的映象集合，F为属性间数据的依赖关系集合。

关系模式简记为
R(U) 或 R(A1，A2，…，An)
其中R为关系名， A1，A2，…，An为属性名。而域名及属向域的映象常常直接说明为属性的类型、长度。

关系模式与关系

• 关系模式是型，关系是值。
• 关系是关系模式在某一时刻的状态或内容。
• 关系模式是静态的、稳定的，关系是动态的、随时间变化的。

2.2 关系操作

2.2.1 基本的关系操作

查询

• 选择、投影、连接、除、并、交、差、笛卡尔积等

数据更新

• 插入、删除、修改

查询的表达能力是其中最主要的部分

关系操作的特点

• 集合操作方式，即操作的对象和结果都是集合，一次一集合。
• 相应地，非关系数据模型的数据操作方式：一次一记录。

2.2.2 关系数据语言的种类

• 关系代数语言
  • 用对关系的运算来表达查询要求
  • 典型代表：IBM-实验性系统ISBL
• 关系演算语言：用谓词来表达查询要求
  • 元组关系演算语言
    • 谓词变元的基本对象是元组变量
    • 典型代表：APLHA, QUEL
  • 域关系演算语言
    • 谓词变元的基本对象是域变量
    • 典型代表：QBE
• 具有关系代数和关系演算双重特点的语言
  • 典型代表：SQL

2.3 关系的完整性

• 数据库的完整性是指数据的正确性和有效性。是指数据是符合现实世界语义、反映当前实际状况的。
• 通过对关系（二维表）中取值的约束，可以保证数据库的完整性，保证数据的正确性。
• 关系模型中有三类完整性约束：
  • 实体完整性
  • 参照完整性
  • 用户定义的完整性

2.3.1 实体完整性

实体完整性规则：若属性A是基本关系R的主属性，则属性A不能取空值。

2.3.2 参照完整性

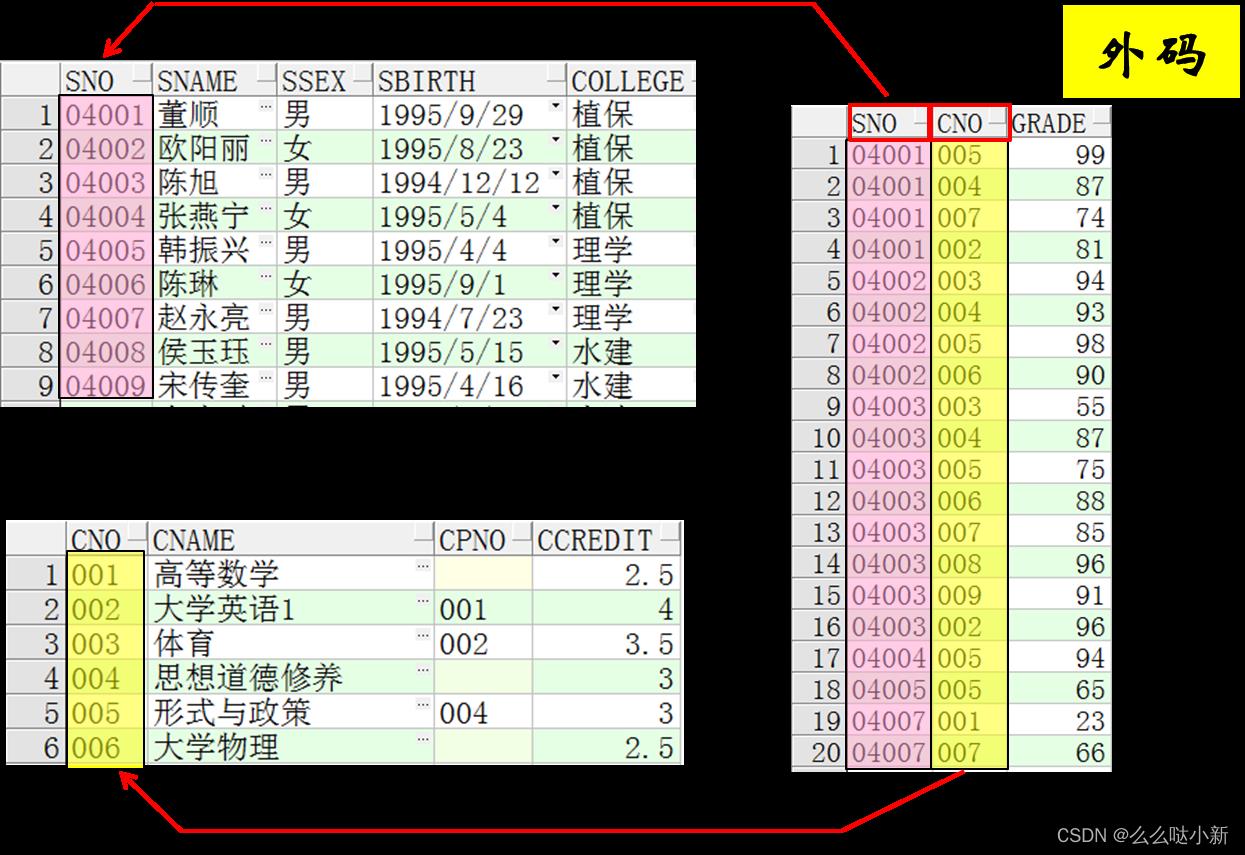
外码：设F是基本关系R的一个或一组属性，但不是关系R的主码。如果F与基本关系S的主码Ks相对应，则称F是基本关系R的外码。

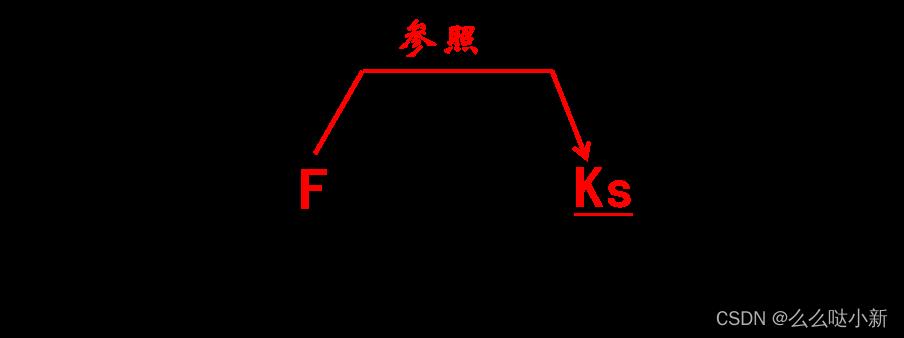
参照完整性规则：若属性F是基本关系R的外码，它与基本关系S的主码Ks相对应，则对于R中每个元组在F上的值必须为：

• 或者取空值；
• 或者等于S中某个元组的主码值。

2.3.3 用户定义的完整性

• 用户定义的完整性是针对某一具体关系数据库的约束条件，反映某一具体应用所涉及的数据必须满足的语义要求。
• 用户定义的完整性没有统一的规则，由数据库设计人员根据具体应用中数据的语义要求来创建。

2.4 关系代数

• 关系代数

  • 一种抽象的查询语言。
  • 用对关系的运算来表达查询。

• 关系代数运算的三个要素

  • 运算对象：关系
  • 运算结果：关系
  • 运算符：四类

• 关系运算符

  • 集合运算符(∩ － ∪ ×)
    • 将关系看成元组的集合；
    • 运算是从关系的“水平”方向即行的角度来进行。
  • 专门的关系运算符(σ π ÷ )
    • 不仅涉及行而且涉及列。

• 比较运算符(＜ ＞ ≥ ≤ ＝ ≠)

  • 辅助专门的关系运算符进行操作。

• 逻辑运算符(∧ ∨ ┓)

  • 辅助专门的关系运算符进行操作。

• 关系代数运算的分类

  • 传统的集合运算
    • 并、差、交、广义笛卡尔积
  • 专门的关系运算
    • 选择、投影、连接、除

2.4.1 传统的集合运算

并、差、交

• R和S满足的条件

  • 具有相同的目n（即两个关系都有n个属性）。
  • 相应的属性取自同一个域。

• R∪S

  • 仍为n目关系，由属于R或属于S的元组组成。
    • 

• R - S

  • 仍为n目关系，由属于R而不属于S的所有元组组成。
    • 

• R ∩ S

  • 仍为n目关系，由既属于R又属于S的元组组成。
    • 

并、交、差举例

• 广义笛卡尔积

  • R：n目关系，k1个元组。

  • S：m目关系，k2个元组。

  • R×S

    • 列：(n+m）列的元组的集合

      • 元组的前n列是关系R的一个元组。

      • 后m列是关系S的一个元组。

    • 行：k1×k2个元组

      • 

广义笛卡尔积举例

2.4.2 专门的关系运算

• 选择
• 投影
• 连接
• 除

1.选择

选择操作是在关系R中选择满足给定条件的诸元组，其表示形式为：

F：选择条件，是一个关系表达式，基本形式为：

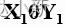
其中：

• θ：运算符（＞，≥，＜，≤，＝或<>）
• X1，Y1等：属性名、常量、简单函数；属性名也可以用它的序号来代替。
• 在基本的选择条件上可以进一步进行逻辑运算，即进行求与(∧)、或(∨) 、非( ┓)。

2.投影

• 投影操作主要是从列的角度进行运算。

• 投影之后不仅取消了原关系中的某些列，而且还可能取消某些元组（避免重复行）。

• 投影运算符的含义

  • 从R中选择出若干属性列组成新的关系。

  • 记作：

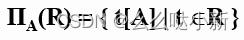
    • 其中A为R中的属性列。

3.连接

也称θ连接：从两个关系的笛卡尔积中选取属性间满足一定条件的元组。

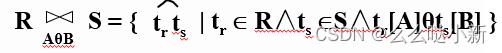
• A和B：分别为R和S上度数相等且可比的属性组。
• θ：比较运算符 。

连接运算从R和S的广义笛卡尔积R×S中选取（R关系）在A属性组上的值与（S关系）在B属性组上值满足比较关系θ的元组。

等值连接

• 什么是等值连接
  • θ为“＝”的连接运算称为等值连接 。
• 等值连接的含义
  • 从关系R与S的广义笛卡尔积中选取A、B属性值相等的那些元组，即等值连接为：.
  • 

自然连接

• 什么是自然连接

  • 自然连接是一种特殊的等值连接。

• 自然连接比等值连接的特殊之处

  • 首先，要求两个关系进行比较的分量必须是同名的属性组；
  • 最后，在等值连接的结果中去掉重复的属性列。

• 若R和S具有相同的属性组B，U为R和S的全体属性集合，则自然连接记作：

  • 

---

• 悬浮元组：在做自然连接时被舍弃的元组称为悬浮元组。
• 外连接：如果把悬浮元组也保存在结果关系中，而在其它属性上填空值，那么这种连接就叫做外连接（outer join）。
• 左外连：如果只保留左边关系R中的悬浮元组就叫做左外连（left outer join）。
• 右外连：如果只保留右边关系S中的悬浮元组就叫做右外连（right outer join）。

4.除

• 象集的概念

  • 给定一个关系R（X，Z），X和Z为属性组。当t[X]=x时，x在R中的象集（Images Set）为：

    • 

  • 它表示R中属性组X上值为x的诸元组在Z上分量的集合。

给定关系R (X，Y) 和S (Y，Z)，其中X，Y，Z为属性组。R中的Y与S中的Y可以有不同的属性名，但必须出自相同的域集。R与S的除运算得到一个新的关系P(X)，P是R中满足下列条件的元组在X属性列上的投影：元组在X上分量值x的象集Yx包含S在Y上投影的集合。

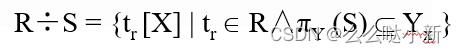
Yx：x在R中的象集，x = tr[X]

一些练习

有三个关系如下：

S(Sno, Sname, Ssex, Sage, Sdept)
学生关系（学号，姓名，性别，年龄，所在学院）
C(Cno, Cname, Cdept, Tname)
课程关系（课程号，课程名，课程开课学院，代课教师）
SC(Sno, Cno, Grade)
选修关系（学号，课程号，成绩）

写出下列查询的关系代数：

1．查询“赵春景”老师所授课程的课程号、课程名。
2．查询选修了课程号为“106” 的学生姓名。
3．查询学生“王小明”所学课程的课程名与任课教师名。
4．查询“理学院”所有学生“数据结构”课程的学号与成绩。
5．查询选修了课程号为“102”或“104”的学生学号。
6．查询至少选修了课程号为“105”和“109”的学生学号。
7．查询不学107课程的学生姓名与年龄。

注意第6题，容易出错

答案在这里

这是根据老师教学内容摘录的部分知识，如果有错误希望大佬可以指出。