Lesson 4.1 逻辑回归模型构建与多分类学习方法

Posted 2023-01-23 虚心求知的熊

文章目录

• 一、广义线性模型（Generalized liner model）的基本定义
• 二、对数几率模型与逻辑回归
• • 1. 对数几率模型（logit model）
  • 2. 逻辑回归与 Sigmoid 函数
  • 3. Sigmoid 函数性质
• 三、逻辑回归模型输出结果与模型可解释性
• 四、多分类学习与多分类逻辑回归
• • 1. OvO 策略
  • 2. OvR 策略
  • 3. MvM 策略

• 首先，我们来讨论关于逻辑回归的基本原理。
• 逻辑回归的基本原理，从整体上来划分可以分为两个部分，其一是关于模型方程的构建，也就是方程的基本形态，当然也包括模型的基本性质及其结果解读；其二则是模型参数求解，即在构建完模型之后如何利用数学工具求解最佳参数。基本划分情况如下：
• 模型构建部分：可以从广义线性回归（Generalized liner model）+ 对数几率函数（logit function）角度理解，也可以从随机变量的逻辑斯蒂分布（logistic distribution）角度出发进行理解。
• 参数求解部分：可以借助极大似然估计（Maximum Likelihood Estimate）方法求解，可以借助 KL 离散度基本理论构建二分类交叉熵损失函数求解。

# 科学计算模块
import numpy as np
import pandas as pd

# 绘图模块
import matplotlib as mpl
import matplotlib.pyplot as plt

# 自定义模块
from ML_basic_function import *

一、广义线性模型（Generalized liner model）的基本定义

• 在前文中我们了解到关于线性回归的局限性，这种局限性的根本由模型本身的简单线性结构（自变量加权求和预测因变量）导致的。
• 如果说线性回归是在一个相对严格的条件下建立的简单模型，那么在后续实践应用过程中，人们根据实际情况的不同，在线性回归的基础上又衍生出了种类繁多的线性类模型。
• 其中，有一类线性模型，是在线性回归基础上，在等号的左边或右边加上了一个函数，从而能够让模型更好的捕捉一般规律，此时该模型就被称为广义线性模型，该函数就被称为联系函数。
• 广义线性模型的提出初衷上还是为了解决非线性相关的预测问题，例如，现在有数据分布如下：

# 数据集特征
np.random.seed(24)
x = np.linspace(0, 4, 20).reshape(-1, 1)
x = np.concatenate((x, np.ones_like(x)), axis=1)
x
#array([[0.        , 1.        ],
#       [0.21052632, 1.        ],
#       [0.42105263, 1.        ],
#       [0.63157895, 1.        ],
#       [0.84210526, 1.        ],
#       [1.05263158, 1.        ],
#       [1.26315789, 1.        ],
#       [1.47368421, 1.        ],
#       [1.68421053, 1.        ],
#       [1.89473684, 1.        ],
#       [2.10526316, 1.        ],
#       [2.31578947, 1.        ],
#       [2.52631579, 1.        ],
#       [2.73684211, 1.        ],
#       [2.94736842, 1.        ],
#       [3.15789474, 1.        ],
#       [3.36842105, 1.        ],
#       [3.57894737, 1.        ],
#       [3.78947368, 1.        ],
#       [4.        , 1.        ]])

# 数据集标签
y = np.exp(x[:, 0] + 1).reshape(-1, 1)
y
#array([[  2.71828183],
#       [  3.35525011],
#       [  4.1414776 ],
#       [  5.11193983],
#       [  6.30980809],
#       [  7.78836987],
#       [  9.61339939],
#       [ 11.86608357],
#       [ 14.64663368],
#       [ 18.07874325],
#       [ 22.31509059],
#       [ 27.54413077],
#       [ 33.99847904],
#       [ 41.96525883],
#       [ 51.79887449],
#       [ 63.93677707],
#       [ 78.91892444],
#       [ 97.41180148],
#       [120.23806881],
#       [148.4131591 ]])

• 此时 x 和 y 的真实关系为 $$y=e^{(x+1)}$$
• 但如果以线性方程来进行预测，即：$$y=w^T\cdot x+b$$
• 当然，我们可以令 $\hat{w}=[w_1,w_2,...w_d,b{]}^T$，$\hat{x}=[x_1,x_2,...x_d,1{]}^T$，从而将上述方程改写为：$$y={\hat{w}}^T\cdot \hat{x}$$
• 则模型输出结果为：

np.linalg.lstsq(x, y, rcond=-1)[0]
#array([[ 30.44214742],
#       [-22.37576724]])

• 即$$y=30.44x-22.38$$
• 则模型预测结果为：

yhat = x[:, 0] * 30.44 - 22.38
yhat
#array([-22.38      , -15.97157895,  -9.56315789,  -3.15473684,
#         3.25368421,   9.66210526,  16.07052632,  22.47894737,
#        28.88736842,  35.29578947,  41.70421053,  48.11263158,
#        54.52105263,  60.92947368,  67.33789474,  73.74631579,
#        80.15473684,  86.56315789,  92.97157895,  99.38      ])

# 观察模型预测和真实结果
plt.plot(x[:, 0], y, 'o')
plt.plot(x[:, 0], yhat, 'r-')

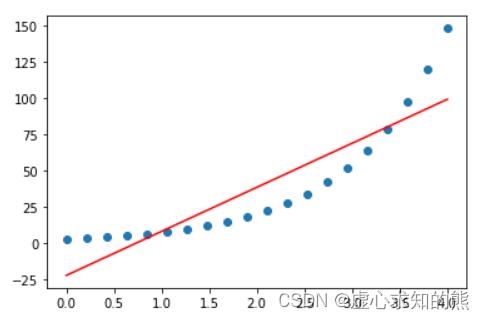
• 能够发现，线性模型预测结果和真实结果差距较大。
• 但此时如果我们在等号右边加上以 $e$ 为底的指数运算，也就是将线性方程输出结果进行以 $e$ 为底的指数运算转换之后去预测 y，即将方程改写为 $$y=e^{({\hat{w}}^T\cdot \hat{x})}$$
• 等价于$$lny={\hat{w}}^T\cdot \hat{x}$$
• 即相当于是线性方程输出结果去预测 $y$ 取以 $e$ 为底的对数运算之后的结果。此时我们可以带入 $lny$ 进行建模。

np.linalg.lstsq(x, np.log(y), rcond=-1)[0]
#array([[1.],
#       [1.]])

• 可得到方程 $$lny=x+1$$
• 等价于 $$y=e^{(x+1)}$$
• 即解出原方程。
• 通过上面的过程，我们不难发现，通过在模型左右两端加上某些函数，能够让线性模型也具备捕捉非线性规律的能力。而在上例中，这种捕捉非线性规律的本质，是在方程加入 ln 对数函数之后，能够使得模型的输入空间（特征所在空间）到输出空间（标签所在空间）进行了非线性的函数映射。
• 而这种连接线性方程左右两端、并且实际上能够拓展模型性能的函数，就被称为联系函数，而加入了联系函数的模型也被称为广义线性模型。广义线性模型的一般形式可表示如下：$$g(y)={\hat{w}}^T\cdot \hat{x}$$
• 等价于 $$y=g^{-1}({\hat{w}}^T\cdot \hat{x})$$
• 其中 $g(\cdot )$ 为联系函数（link function），$g^{-1}(\cdot )$ 为联系函数的反函数。而如上例中的情况，也就是当联系函数为自然底数的对数函数时，该模型也被称为对数线性模型（logit linear model）。
• 这里需要注意，一般来说广义线性模型要求联系函数必须是单调可微函数。
• 从广义线性模型的角度出发，当联系函数为 $g(x)=x$ 时，$g(y)=y={\hat{w}}^T\cdot \hat{x}$，此时就退化成了线性模型。而能够通过联系函数拓展模型捕捉规律的范围，这也就是广义的由来。

二、对数几率模型与逻辑回归

• 逻辑回归也被称为对数几率回归。接下来，我们从广义线性模型角度理解逻辑回归。

1. 对数几率模型（logit model）

• 几率（odd）与对数几率
• 几率不是概率，而是一个事件发生与不发生的概率的比值。
• 假设某事件发生的概率为 p，则该事件不发生的概率为 1-p，该事件的几率为：$$odd(p)=\frac{p}{1-p}$$
• 在几率的基础上取（自然底数的）对数，则构成该事件的对数几率（logit）：$$logit(p)=ln\frac{p}{1-p}$$
• 这里需要注意的是，logit 的是 log unit 对数单元的简写，和中文中的逻辑一词并没有关系。对数几率模型也被称为对数单位模型（log unit model）。
• 对数几率模型
• 如果我们将对数几率看成是一个函数，并将其作为联系函数，即 $g(y)=ln\frac{y}{1-y}$，则该广义线性模型为： g ( y ) = l n y 1 − y = w ^ T ⋅ x ^ g(y)=ln\\fracy1-y=\\hat w^T \\cdot \\hat x g(y)=ln1−yy​=w^以上是关于Lesson 4.1 逻辑回归模型构建与多分类学习方法的主要内容，如果未能解决你的问题，请参考以下文章

  机器学习系列7 基于Python的Scikit-learn库构建逻辑回归模型

  小白学习PyTorch教程七基于乳腺癌数据集​​构建Logistic 二分类模型

  TensorFlow逻辑回归原理与实现（超详细）

  R语言基于h2o包构建二分类模型：使用h2o.glm构建正则化的逻辑回归模型使用h2o.auc计算模型的AUC值

  机器学习6逻辑回归算法

  机器学习逻辑回归