TensorFlow逻辑回归原理与实现(超详细)
Posted ZSYL
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了TensorFlow逻辑回归原理与实现(超详细)相关的知识,希望对你有一定的参考价值。
逻辑回归原理与实现
学习目标
- 目标
- 知道逻辑回归的算法计算输出、损失函数
- 知道导数的计算图
- 知道逻辑回归的梯度下降算法
- 知道多样本的向量计算
- 应用
- 应用完成向量化运算
- 应用完成一个单神经元神经网络的结构
1. 神经网络基础
1.1 Logistic回归
逻辑回归是一个主要用于二分分类类的算法。那么逻辑回归是给定一个 x x x , 输出一个该样本属于1对应类别的预测概率 y ^ = P ( y = 1 ∣ x ) \\hat{y}=P(y=1|x) y^=P(y=1∣x)。
Logistic 回归中使用的参数如下:


e − z e^{-z} e−z 的函数如下:

例如:
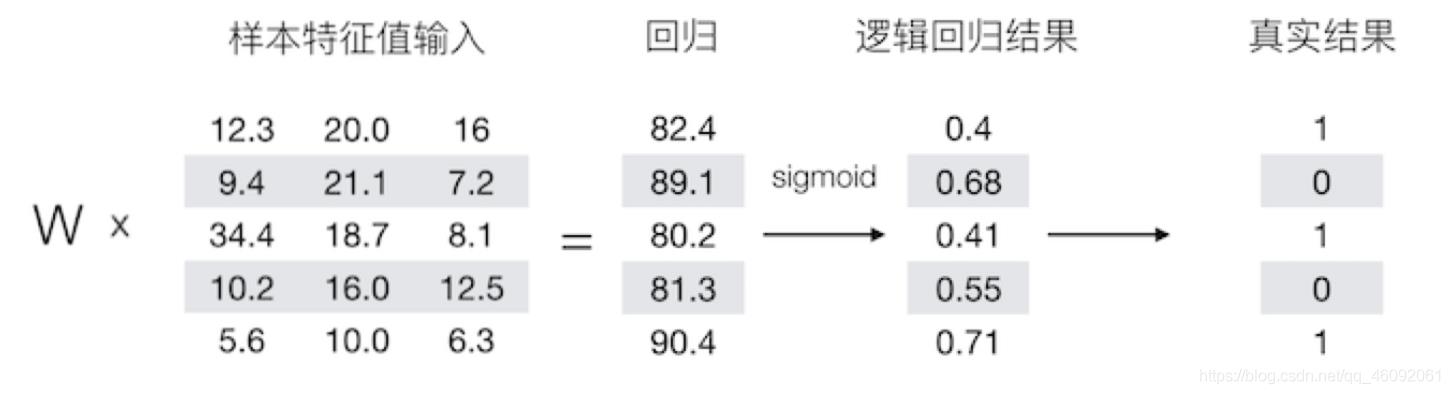
1.2 逻辑回归损失函数
损失函数(loss function) 用于衡量预测结果与真实值之间的误差。最简单的损失函数定义方式为平方差损失:
L ( y ^ , y ) = 1 2 ( y ^ − y ) 2 L(\\hat{y},y) = \\frac{1}{2}(\\hat{y}-y)^2 L(y^,y)=21(y^−y)2
逻辑回归一般使用 L ( y ^ , y ) = − ( y log y ^ ) − ( 1 − y ) log ( 1 − y ^ ) L(\\hat{y},y) = -(y\\log\\hat{y})-(1-y)\\log(1-\\hat{y}) L(y^,y)=−(ylogy^)−(1−y)log(1−y^)
该式子的理解:
- 如果y=1,损失为 − log y ^ - \\log\\hat{y} −logy^,那么要想损失越小, y ^ \\hat{y} y^的值必须越大,即越趋近于或者等于1
- 如果y=0,损失为 1 log ( 1 − y ^ ) 1\\log(1-\\hat{y}) 1log(1−y^),那么要想损失越小,那么 y ^ \\hat{y} y^ 的值越小,即趋近于或者等于0
损失函数是在单个训练样本中定义的,它衡量了在单个训练样本上的表现。代价函数(cost function)衡量的是在全体训练样本上的表现,即衡量参数 w 和 b 的效果,所有训练样本的损失平均值
J ( w , b ) = 1 m ∑ i = 1 m L ( y ^ ( i ) , y ( i ) ) J(w,b) = \\frac{1}{m}\\sum_{i=1}^mL(\\hat{y}^{(i)},y^{(i)}) J(w,b)=m1i=1∑mL(y^(i),y(i))
2. 梯度下降算法
目的:使损失函数的值找到最小值
方式:梯度下降
函数的**梯度(gradient)**指出了函数的最陡增长方向。梯度的方向走,函数增长得就越快。那么按梯度的负方向走,函数值自然就降低得最快了。模型的训练目标即是寻找合适的 w 与 b 以最小化代价函数值。假设 w 与 b 都是一维实数,那么可以得到如下的 J 关于 w 与 b 的图:

可以看到,成本函数 J 是一个凸函数,与非凸函数的区别在于其不含有多个局部最低。
参数w和b的更新公式为:
w : = w − α d J ( w , b ) d w w := w - \\alpha\\frac{dJ(w, b)}{dw} w:=w−αdwdJ(w,b), b : = b − α d J ( w , b ) d b b := b - \\alpha\\frac{dJ(w, b)}{db} b:=b−αdbdJ(w,b)
注:其中 α 表示学习速率,即每次更新的 w 的步伐长度。当 w 大于最优解 w′ 时,导数大于 0,那么 w 就会向更小的方向更新。反之当 w 小于最优解 w′ 时,导数小于 0,那么 w 就会向更大的方向更新。迭代直到收敛。
通过平面来理解梯度下降过程:

3. 导数
理解梯度下降的过程之后,我们通过例子来说明梯度下降在计算导数意义或者说这个导数的意义。
3.1 导数
导数也可以理解成某一点处的斜率。斜率这个词更直观一些。
- 各点处的导数值一样
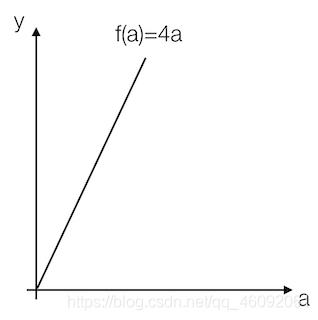
我们看到这里有一条直线,这条直线的斜率为4。我们来计算一个例子
例:取一点为a=2,那么y的值为8,我们稍微增加a的值为a=2.001,那么y的值为8.004,也就是当a增加了0.001,随后y增加了0.004,即4倍
那么我们的这个斜率可以理解为当一个点偏移一个不可估量的小的值,所增加的为4倍。
可以记做 f ( a ) d a \\frac{f(a)}{da} daf(a)或者 d d a f ( a ) \\frac{d}{da}f(a) dadf(a)
- 各点的导数值不全一致

例:取一点为a=2,那么y的值为4,我们稍微增加a的值为a=2.001,那么y的值约等于4.004(4.004001),也就是当a增加了0.001,随后y增加了4倍
取一点为a=5,那么y的值为25,我们稍微增加a的值为a=5.001,那么y的值约等于25.01(25.010001),也就是当a增加了0.001,随后y增加了10倍
可以得出该函数的导数2为2a。
- 更多函数的导数结果
| 函数 | 导数 |
|---|---|
| f ( a ) = a 2 f(a) = a^2 f(a)=a2 | 2 a 2a 2a |
| f ( a ) = a 3 f(a)=a^3 f(a)=a3 | 3 a 2 3a^2 3a2 |
| f ( a ) = l n ( a ) f(a)=ln(a) f(a)=ln(a) | 1 a \\frac{1}{a} a1 |
| f ( a ) = e a f(a) = e^a f(a)=ea | e a e^a ea |
| σ ( z ) = 1 1 + e − z \\sigma(z) = \\frac{1}{1+e^{-z}} σ(z)=1+e−z1 | σ ( z ) ( 1 − σ ( z ) ) \\sigma(z)(1-\\sigma(z)) σ(z)(1−σ(z)) |
| g ( z ) = t a n h ( z ) = e z − e − z e z + e − z g(z) = tanh(z) = \\frac{e^z - e^{-z}}{e^z + e^{-z}} g(z)=tanh(z)=ez+e−zez−e−z | 1 − ( t a n h ( z ) ) 2 = 1 − ( g ( z ) ) 2 1-(tanh(z))^2=1-(g(z))^2 1−(tanh(z))2=1−(g(z))2 |
3.2 导数计算图
那么接下来我们来看看含有多个变量的到导数流程图,假设
J
(
a
,
b
,
c
)
=
3
(
a
+
以上是关于TensorFlow逻辑回归原理与实现(超详细)的主要内容,如果未能解决你的问题,请参考以下文章 深度学习原理与框架-Tensorflow卷积神经网络-神经网络mnist分类