递推的递推算法

Posted 2023-04-23

参考技术A

【例1】
植树节那天，有五位同学参加了植树活动，他们完成植树的棵树都不相同。问第一位同学植了多少棵时，他指着旁边的第二位同学说比他多植了两棵；追问第二位同学，他又说比第三位同学多植了两棵；... 如此，都说比另一位同学多植两棵。最后问到第五位同学时，他说自己植了10棵。到底第一位同学植了多少棵树？
分析：设第一位同学植树的棵树为a1,欲求a1，需从第五位同学植树的棵数a5入手，根据“多两棵”这个规律，按照一定顺序逐步进行推算：
(1) a5=10;
(2) a4=a5+2=12;
(3) a3=a4+2=14;
(4) a2=a3+2=16;
(5) a1=a2+2=18;
Pascal程序：
Program Examl;
Var i,a:byte;
begin
a:=10;
for i:= 1 to 4 do
a:=a+2;
writeln('The Num is' ,a);
readln;
end.
本程序的递推运算可用下图示表示：
初始值a:=10 ----- i=1,a=a+2(12) ----- i=2,a=a+2(14) ------ i=3,a=a+2(16) ----- i=4,a=a+2(18) ---- 输出a值
例2：
十本不同的书放在书架上。现重新摆放，使每本书都不在原来放的位置。有几种摆法？
当n个编号元素放在n个编号位置,元素编号与位置编号各不对应的方法数用M(n)表示,那么M(n-1)就表示n-1个编号元素放在n-1个编号位置,各不对应的方法数,其它类推.
第一步,把第n个元素放在一个位置,比如位置k,一共有n-1种方法;
第二步,放编号为k的元素,这时有两种情况.1,把它放到位置n,那么,对于剩下的n-2个元素,就有M(n-2)种方法;2,不把它放到位置n,这时,对于这n-1个元素,有M(n-1)种方法;
综上得到
M(n)=(n-1)[M(n-2)+M(n-1)]
递推算法以初始（起点）值为基础，用相同的运算规律，逐次重复运算，直至运算结束。这种从“起点”重复相同的方法直至到达一定“边界”，犹如单向运动，用循环可以实现。递推的本质是按规律逐次推出（计算）先一步的结果。

JC2：递推，递归与分治

递推，递归与分治[待完成]

递推的定义

定义：已知初始值F1，通过递推关系式Fn=g(Fn-1)求出最终结果Fn的递推方式称为顺推法；同理，把已知最终结果为Fn，通过递推关系式Fn-1=g＇(Fn)求出初始值F1的递推方式称为倒推法。

 

模板：

f[0]=0; f[1]=1;

for(int i=1; i<=n; i++) f[i]=f[i-1]+f[i-2];

具体步骤

找到初始状态 找到递推公式 开始循环算

经典问题

抽屉原理 加法原理 乘法原理 容斥原理 卡特兰数

递归

递归算法

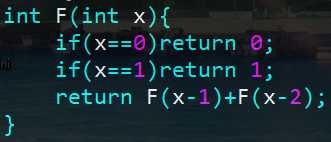
设一个未知函数f，用其自身构成的已知函数g来定义：

f(n)=g(n,f(n-1)) n>0

f(0)=a n=0

描述递归定义的函数或求解递归问题的过程称为递归算法