面试时如何完整精确的回答动量下降法(Momentum)和Adam下降法的原理

Posted 2023-04-20

参考技术A 在人工智能算法中，最终的目标都是找到一个最优的模型，而如何找到这个最优模型的参数一般有两种方法：第一就是等式求解，这个只对一部分简单的模型有效果，当模型的复杂度上升和参数变多时，求解将会变的极其困难，甚至不存在等式解。所以那么这里也就有第二种方法：梯度求解，这是一种利用梯度来一步步接近最优解。其中最有名和最普遍的有批量梯度下降法(BGD),随机梯度下降法(SGD),小批量梯度下降法。

上面三种梯度下降我就不再细讲，本质都是一样的，只不过每次更新利用的数据数量不一样，批量梯度下降每次优化时，使用的都是全部的数据集，所以计算量大，所以当数据量太大时，算法收敛的速度会很慢，但是他可以保证每次都朝着最优点的方向下降，不易受噪声的干扰。随机梯度下降则是每一次都使用一个数据来进行下降，所以他的下降过程震荡会很明显，但是收敛速度会很快，而且经实验证明他会朝着最优点收敛。小批量随机梯度下降则是结合了前两个算法的优点，收敛速度快且受噪声的影响较小。

这里重点介绍一下动量下降法，他的更新公式：

ut = γut−1 + ηgt

wt+1 =wt −ut.

上面的两个公式，如果γ=0，那么这就是一个SGD，当γ>0,那么他就是动量下降法，他有以下的优点：

他的更新公式为：

上面的1式，就是动量下降法的第一个式子，优点那就是跟前面的一样，那么这里Adam的优点就是，这里的3式和4式了，这里用到了梯度的平方，然后根据第5式，这个是对学习率的一个更新，根据3式可知，在学习过程中，随着梯度的累加，vt 将会增加，那么学习率也将逐渐的变小，从而减轻在最优点附近震荡。这和我们的直觉也是一致的，当离得最优点较远的时候，学习率应当大一些从而加快学习，而当离最优点较近时，则学习率应当更小一些，从而更好的找到最优点。

---------------------

原文：https://blog.csdn.net/tang_1994/article/details/87692843

深度学习优化算法之动量法[公式推导]（MXNet）

我们在前面的文章中熟悉了梯度下降的各种形态，深度学习优化算法之(小批量)随机梯度下降（MXNet），也了解了梯度下降的原理，由每次的迭代，梯度下降都根据自变量的当前位置来更新自变量，做自我迭代。但是如果说自变量的迭代方向只是取决于自变量的当前位置的话，这可能会带来一些问题。比如我们来看下函数 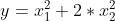 的走势，现在我们来看下这个函数其系数为0.1的情况 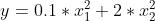在学习率变化时，将会发生什么变化。

从eta=0.4一个比较合适的学习率开始：

import d2lzh as d2l
from mxnet import nd

eta=0.4

def f_2d(x1,x2):
    return 0.1*x1**2 + 2*x2**2

def gd_2d(x1,x2,s1,s2):
    return (x1-eta*0.2*x1,x2-eta*4*x2,0,0)

d2l.show_trace_2d(f_2d,d2l.train_2d(gd_2d))
    
#epoch 20, x1 -0.943467, x2 -0.000073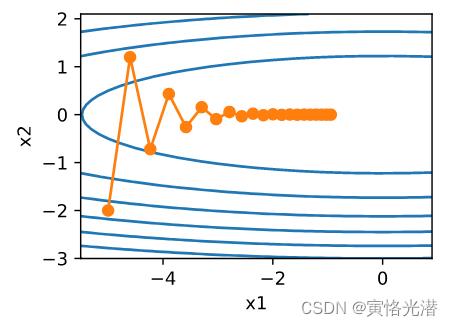

 

图中可以看出，同一个位置上，目标函数在竖直方向(x2轴方向)比在水平方向(x1轴方向)的斜率的绝对值更大，换句话说就是自变量的更新会使自变量在竖直方向比在水平方向移动幅度更大。
我们将学习率调大一点：eta=0.6

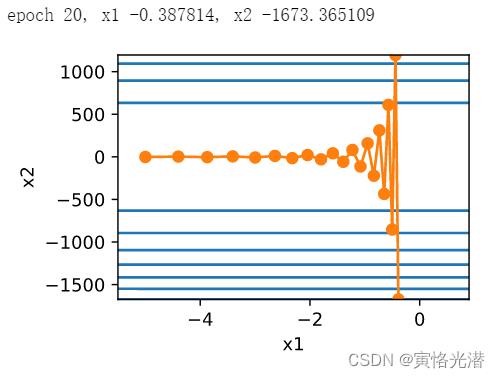
我们发现自变量在竖直方向不断越过最优解并逐渐发散了。

动量法

那上面这个问题，我们通过动量法来处理，在前面的文章也有介绍，这里算是一种新的学习与巩固，更重要的是了解为什么动量法能够处理这种上下方向的偏幅。
那很明显上面存在的问题就是自变量在竖直方向的更新不一致，时正时负，找到问题所在之后，那我们就只需要解决这个方向一致的问题就好办了。

对于动量法的推导，我们从指数加权移动平均(Exponentially Weighted  Moving Average)来理解它，还是画图来直观看下其推导过程：

 

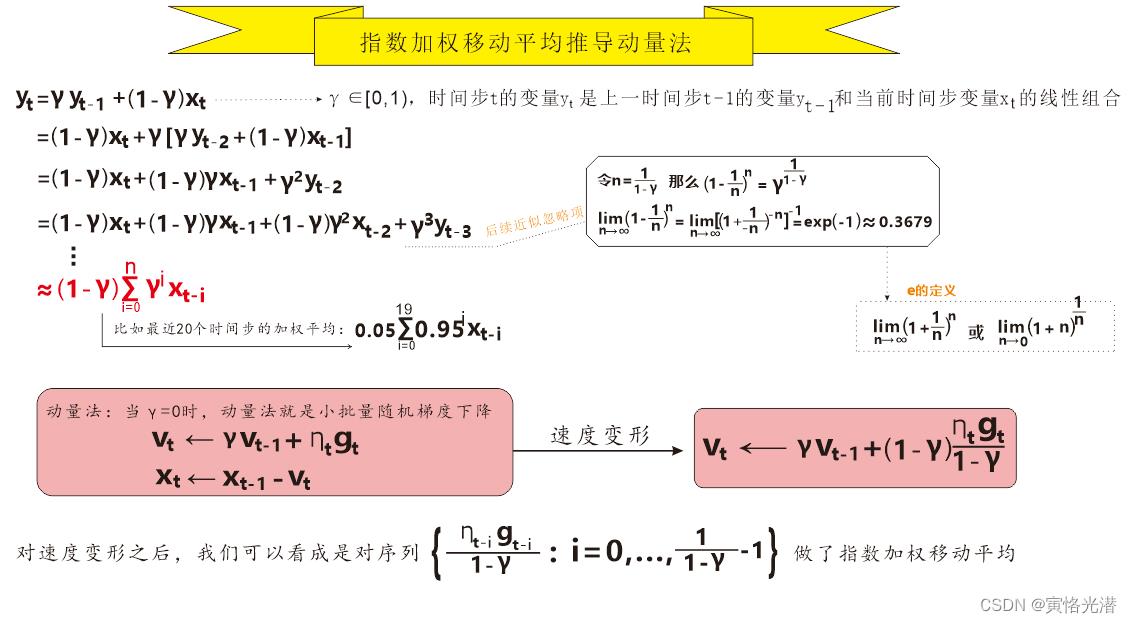
然后我们通过代码来看下实际情况：

eta,gamma=0.4,0.5

def f_2d(x1,x2):
    return 0.1*x1**2 + 2*x2**2

#当gamma=0时，就是小批量随机梯度下降
def momentum_gd_2d(x1,x2,v1,v2):
    v1=gamma*v1 + eta*0.2*x1
    v2=gamma*v2 + eta*4*x2
    return x1-v1,x2-v2,v1,v2

d2l.show_trace_2d(f_2d,d2l.train_2d(momentum_gd_2d))

#epoch 20, x1 -0.062843, x2 0.001202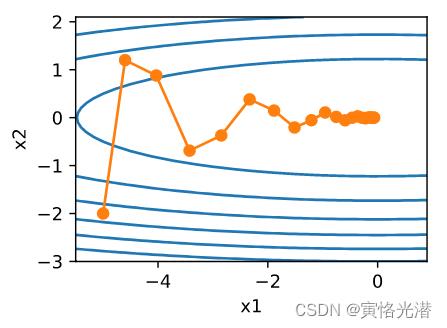

 

图中可以看出使用动量法之后在竖直方向上的移动更加平滑了，而且在水平方向也更快逼近最优解。
然后将学习率调大到0.6，也没有出现发散的情况。

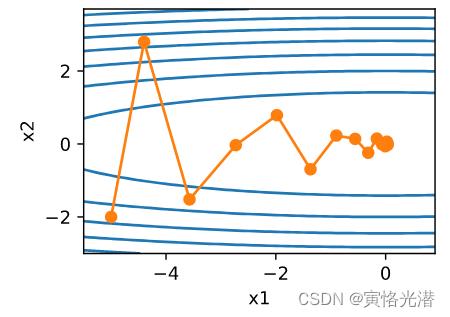
飞机机翼噪音测试

import d2lzh as d2l
from mxnet import nd

#使用飞机噪音数据集来测试
#https://download.csdn.net/download/weixin_41896770/86513479
features,labels=d2l.get_data_ch7()#1503x5,1503

#速度变量用更广义的状态变量states表示
def init_momentum_states():
    v_w=nd.zeros((features.shape[1],1))
    v_b=nd.zeros(1)
    return (v_w,v_b)

def sgd_momentum(params,states,hyperparams):
    for p,v in zip(params,states):
        v[:]=hyperparams['momentum']*v +hyperparams['lr']*p.grad
        p[:]-=v

d2l.train_ch7(sgd_momentum,init_momentum_states(),'lr':0.02,'momentum':0.5,features,labels)
#loss: 0.249161, 0.171031 sec per epoch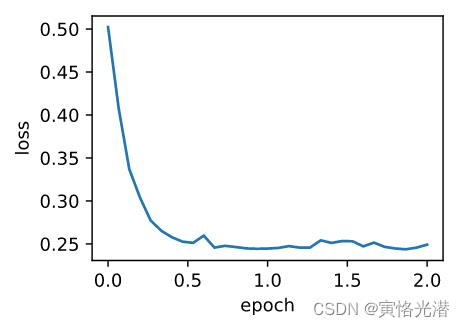

#看做特殊的小批量随机梯度下降
#最近2个时间步的2倍小批量梯度的加权平均
#d2l.train_ch7(sgd_momentum,init_momentum_states(),'lr':0.02,'momentum':0.5,features,labels)
#最近10个时间步的10倍小批量梯度的加权平均,1/(1-0.9)
d2l.train_ch7(sgd_momentum,init_momentum_states(),'lr':0.02,'momentum':0.9,features,labels)
loss: 0.259894, 0.177999 sec per epoch

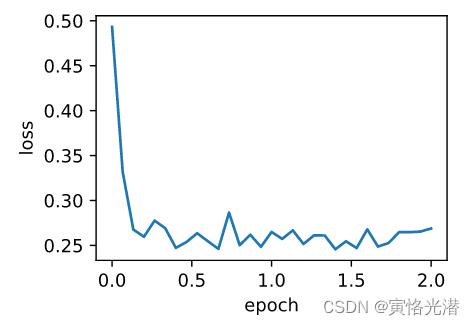
图中可以看出后期的迭代不够平滑，因为10倍小批量梯度比2倍小批量梯度大了5倍，我们将学习率调小5倍试下：

#学习率调下5倍，从0.02到0.004
d2l.train_ch7(sgd_momentum,init_momentum_states(),'lr':0.004,'momentum':0.9,features,labels)
#loss: 0.243785, 0.181000 sec per epoch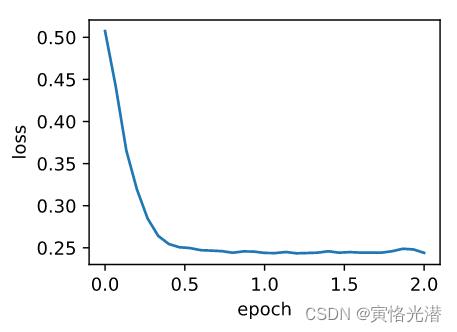

#简洁实现
d2l.train_gluon_ch7('sgd','learning_rate':0.004,'momentum':0.9,features,labels)

动量法的出现主要是解决相邻时间步的自变量的在更新方向上的问题，使得它们更加趋向一致，因为它将过去时间步的梯度做了加权平均，而不仅仅是关注当前变量梯度的位置。