指数加权平均动量梯度下降法RMSpropAdam优化算法
Posted 劳埃德·福杰
tags:
篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了指数加权平均动量梯度下降法RMSpropAdam优化算法相关的知识，希望对你有一定的参考价值。
1.指数加权平均(exponentially weighted averages)
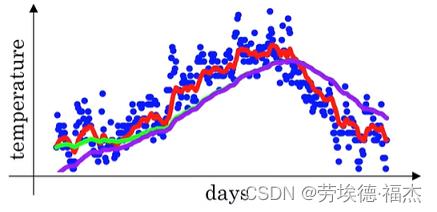
这里有一年的温度数据。
如果想计算温度的趋势，也就是局部平均值(local average)，或者说移动平均值(moving average)，怎么做？
：当天的温度，
：从当天开始计算前
天的平均温度，
：从昨天开始计算前天的平均温度。
比如，β=0.9，计算的就是前10天的平均温度，如下图红线所示。β=0.98，计算的就是前50天的平均温度，如下图绿线所示。
为什么是天？
，
，
...
...
这些项的系数呈指数级减少
0.37，
当β->1，选定为分界线，从
开始，以后的项都可忽略不计，(1-β)=
。
例：β=0.9，10为分界线，
(1-0.9)
0.9
0.
...+0.
...
。
β=0.98，50为分界线，(1-0.98)0.
0.
...+0.
...
。
偏差修正(Bias correction)
β=0.98，如果没有进行偏差修正，得到的其实是下图的紫线。
，
0.02
，
=0.98x0.02+0.02
=5，
，算局部平均值的时候，不太合理，偏小。
所以，在估测初期要进行一个修正，公式：
例：t=2，要修正为
，β=0.98
当t越来越大的时候，就近似等于，上图的紫线就和绿线重合了，修正偏差的作用也就不大了。
所以，如果你关心初始时期的偏差，偏差修正能让你在早期获得更好的估测。不在乎早期的偏差，不做修正也问题不大。
指数加权平均优点是只会占很少的内存，计算的时候只需要一行代码，需要知道的信息很少。计算精度肯定不如直接计算前n天的均值，但是后者要保存前n天的数据，更占内存。
2.动量梯度下降法(Gradient descent with momentum)
动量梯度下降法(红线)要快于标准的梯度下降法(蓝线)。
每次迭代，在现有的mini-batch上计算dW，db，更新参数。等式右边的
其实是上一状态的值。
两个超参数(hyperparameter)：α(学习率)、β(控制着指数加权平均)，β常见值等于0.9
3.RMSprop
RMSprop算法同样能加速梯度下降。
每次迭代，在现有的mini-batch上计算dW，db，更新参数。
，
w:=
，b:=
RMS：Root Mean Square，均方根
4.Adam优化算法(optimization algorithm)
该算法实际上是将momentum和RMSprop这两种算法结合起来，也是为了加速梯度下降，应用广泛。
每次迭代，在现有的mini-batch上计算dW，db，更新参数。
，
，
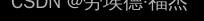偏差修正：
，
，
，
w:=
，b:=
超参数：学习率α：需要调整、
常用值为0.9、
常用值为0.999、ε常用值为
以上是关于指数加权平均动量梯度下降法RMSpropAdam优化算法的主要内容，如果未能解决你的问题，请参考以下文章