高分求2007高教社杯数学建模竞赛B题论文

Posted 2023-04-11

希望各位大虾提供论文下载链接，谢谢。

2007高教社杯全国大学生数学建模竞赛B题论文

公共交通网络模型

摘 要：

明年8月第29届奥运会将在北京举行，届时有大量观众到现场观看奥运比赛，这将对北京的交通带来巨大的影响。本文以给出的北京地区公交路线为参考资料，根据公交网络换乘问题构建了公共交通网络模型。对三个问题的解决方案如下：

（1）针对问题1，本文首先利用MATLAB编程将公交线路读出，求出各站点间的邻接矩阵。再根据所求的邻接矩阵。对求得的邻接矩阵进行处理；判断起点和终点之间有没有直达的线路，如有就确定为最优线路，没有就在通过程序寻找一个合适的数值（记为M）作为限制（即找出邻接点最多的那部分站点），找出通过次数超过这个数值的站点。

下一步则寻找换乘站点。通过把求得的站点与要求的起点和终点，建立循环逐个修改开始站点与最终站点的值可求出通过各站点的路线，再将经过所求得的站点的路线与经过起点和终点的路线进行比较，寻找相同的路线，若存在，则这个站点可以作为所给的这对起点与终点的中转站（但根据人们乘车的习惯，假设中转的次数不超过2次）。如果的站点中无法找到中转站，则调整M的值，直到可以找到可行的乘车路线为止。

根据得到的可行乘车线路，利用路过分别与费用和时间的函数关系，计算出按照吸收较小转车次数的原则，比较用钱少、费时少的线路，最终得到最优的乘车方案。

（2）针对问题2，将换乘地铁站和公汽站视为对等的，与问题1相似，利用相同的方法求出最优线路，但是情况比问题1更复杂，特别是地铁与地铁之间还可以换乘，这需要单独进行考虑。此时，站点数、费用和时间的函数发生了变化，因此，利用新的函数表达式求解再比较得到最优线路。

（3）针对问题3，考虑步行时，可先利用图论中的Floyd算法求出任意两站点间的最短道路，并在此基础上求出这段路步行所需要的时间。再在第二问的基础上，对时间加一个阈值T。当计算出的两点间最短路的步行时间<阈值T时，就选择步行，否则，选择问题2中求得的最优线路。

本文所考虑的算法，可以查询任意两个站点间的乘车最优路径。

关键词：MATLAB程序、公交换乘、限制求解、Floyd算法、最优线路

一、问题重述

北京申奥的成功，对北京市的交通系统提出了更高的要求。依据国外举办奥运会的经验教训来看，奥运期间交通状况是否良好，交通管理是否高效，是关系奥运盛会能否圆满成功举办的举足轻重的条件之一。因此，必须在全面调研基础上，制定切实可行的交通规划及管理策略，为奥运会的成功保驾护航。

在观众的交通行为中，轨道站点、外围停车场和专用巴士的换乘，是整个交通链的重要环节，一旦出现交通瓶颈，其向上游反馈形成的阻塞波(或者称为交通扰动)会溯源而上并且影响加剧，最终造成主会场人员疏散的延误和交通设施服务水平的降低以及一定程度上的混乱和连带的不可估量的经济损失、负面的社会影响。因此应从系统全局考虑进行换乘系统规划，保证观众出行全过程的流畅。

二、模型假设

1、乘客到起始站可以直接选择公汽或地铁班次上车，即不记在起始站的等待时间。

2、在实际过程中，对于公交（包括公汽与地铁）可能要换车2次以上，用户已无法容忍，视为无法到达。（因为如果他们之间换乘就使得费用增大了很多，这是人们不愿意看到的，且一般只坐地铁是无法到达终点站的，所以还要再换乘其他的工具，换乘次数太大我们也不再将其纳入考虑的范围）。

3、相邻地铁站平均行驶时间(包括停站时间)： 2.5分钟。

4、相邻公汽站平均行驶时间(包括停站时间)： 3分钟。

5、公汽换乘公汽平均耗时： 5分钟(其中步行时间2分钟)。

6、地铁换乘地铁平均耗时： 4分钟(其中步行时间2分钟)。

7、地铁换乘公汽平均耗时： 7分钟(其中步行时间4分钟)。

8、公汽换乘地铁平均耗时： 6分钟(其中步行时间4分钟)。

9、公汽票价：分为单一票价与分段计价两种，标记于线路后；其中分段计价票价为：0～20站：1元；21～40站：2元；40站以上：3元。

10、地铁票价：3元（无论地铁线路间是否换乘）。

11、已知所有站点之间的步行时间。

12、同一地铁站对应的任意两个公汽站之间可以通过地铁站换乘(无需支付地铁费)。

13、郊县和繁华地区公交车站的间隔大概一致。

三、符号说明

1、 表示第一问中从起点站到终点站所用的总时间。

2、 表示表示第一问中从起点站到终点站经过的总站点数。

3、M表示求取局部最优解的限制值。

4、T表示判断是坐车还是步行的阈值，但这个值因人而易。

四、问题的分析

文献[2]对公交乘客的出行心理进行了研究，其结果表明，“换乘次数”是大部分公交乘客在选择出行路线时首先考虑的因素，其次是出行耗时和距离长短。而出行耗费的时间与换乘的次数，及等车的时间以及距离的长短密切相关。因此，对于出行耗时和距离长短，转化为换乘次数最少的基础上出行距离最短的问题。对公交换乘的问题进行

研究，首先就是要解决公共交通网络模型如何合理地表述；其次是公交换乘问题的解决思想。

公共交通网络不同于一般的道路交通网络，在许多书籍文献中都对公共交通网络的特点进行了阐述，如网络的连通性不同于普通道路网，结点有其空间位置特性和一对多的属性等，并分析了弧段的特性及有向线的性质。对于公交网络的特点不再赘述。

在GIS网络分析中，公共交通网络可以映射为一个有向图。根据公共交通网络的特点，把公交网络模型映射为，其中，G为有向赋权图；V表示网络上所有结点即公交站点的集合，一个公交站点可能是多条公交线路的上下客站点；表示网络边(连接公交线路上两个公交站点之间的弧段)的集合，若A站点与B站点是n条线路的相邻上下客站点，那么A与B之间至多有2n条连接边：R表示网络上连接起始点和目标点间所有结点的公交线路的集合； 是结点的非负权值；是边的非负权值[4]。最优出行路径就是指乘客从起始点到目标点所选择的一系列连通结点组成的距离最短的路段及最少换乘的公交线路的集合。[3] 参考技术A 可看看下面两个网站：
http://mcm.edu.cn/mcm07/format2007.doc
http://blog.sina.com.cn/s/blog_4d34f48401000abr.html
另外你可以尝试通过百度搜索一下，应该有你需要的，希望能帮上你！本回答被提问者采纳 参考技术B 帮不上啊~！ 参考技术C 百度一下

2022数学建模国赛高教社杯C题思路

2022年高教社杯数学建模竞赛已经开赛，今天9.15号作为比赛的第一天，大家不要急于选题。首先大家应该根据自己队伍以往的训练决定择题。再根据题目的具体情况进行选题。我将为大家进行分析C题的赛题赛题浅评，帮助大家更好的选题。这里将为大家进行分析每个题目的难度，涉及到的模型以及具体的难点等。以及后续更新各个题目的选择比例。本次主要分析C题，预计C题也将是选择人数最多的一道题目。稍后应该也会发布C题的半成品论文希望对大家有所帮助。C题论文指导已经发布

C 题 古代玻璃制品的成分分析与鉴别

C题作为国赛中最简单的一道题目，今年依旧持续发力，C题为成分分析类型题目，该问题与2021年国赛B题相似，C题以古代玻璃制品为背景，需要我们根据给出的数据分析。我们可以看作为数据处理类型+数据预测类型题目。

问题 1 对这些玻璃文物的表面风化与其玻璃类型、纹饰和颜色的关系进行分析；结合玻璃的类型，分析文物样品表面有无风化化学成分含量的统计规律，并根据风化点检测数据，预测其风化前的化学成分含量。

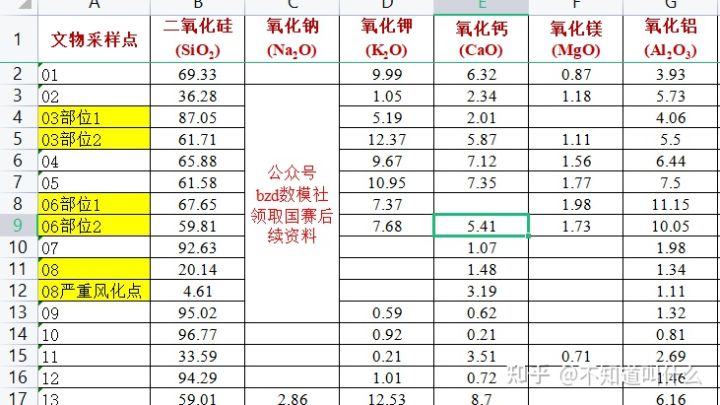
对于问题一，题目要求我们根据这表1中的表面风化与其玻璃类型、纹饰和颜色的关系进行分析，如下图1所示。对于后半问的问题就会涉及到表单2，需要我们分析表面有无风化化学成分含量的统计规律，根据给出的表单2中的数据预测其风化前的化学成分含量。首先对于前半问的关系分析，这里我认为可以直接使用相关性分析，person检验等方式，这里稍后会为大家补充相应的代码。根据得到的结果即可进行关系分析。对于后半问，预测化学含量。我们可以使用很多种预测方式进行，这里我比较倾向于2021年国赛B的通用方式，建立多元线性回归模型利用不同指标的关系对风化前的化学成分利用构建的函数表达式进行求解。

问题一遗留问题，这里稍后会大家解说， 数据处理的各项细节，例如如何用序号表示同一文物不同部位等数据处理细节。后半问预测化学含量的其他使用方式。

问题 2 依据附件数据分析高钾玻璃、铅钡玻璃的分类规律；对于每个类别选择合适的化学成分对其进行亚类划分，给出具体的划分方法及划分结果，并对分类结果的合理性和敏感性进行分析。

对于问题二，就需要我们整理表单1表单2的数据对高钾玻璃、铅钡玻璃相关的数据进行分析。这里依旧可以使用问题一中我们已经使用的相关性检验，对结果进行分类。再对于不用的玻璃类型内，利用相关性分析的结果再次进行分析。这是我认为C题问题二最简单的做法，但是这样做虽然合情合理，但是再得分上可能会有所低。因为这应该是大多数人都能考虑到的方法。因此，我认为也可以使用其他分类方式例如聚类分析等，这一部分稍后我会为大家进行补充。大家可以私信或者留言，在评论区讨论一下。

问题 3 对附件表单 3 中未知类别玻璃文物的化学成分进行分析，鉴别其所属类型，并对分类结果的敏感性进行分析。

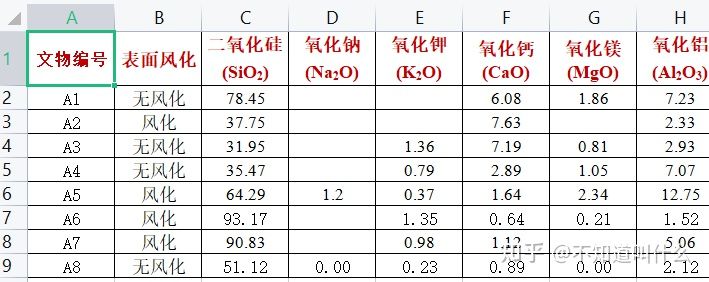
问题三就是这几年建模国赛尤为重视的一点，灵敏度分析，近几年的评分细则中加入了以往所有没有灵敏度分析。因此，这一次也是近年来国赛的新点、热点。对于问题三，需要我们用到表单3，如下图所示。对于问题三我们可以沿用问题一中所建立的多元线性方程，对玻璃类型进行计算，从而实现整个问题的模型完整性。也可以使用其他的方式进行判断玻璃类型。这里我个人还是比较建议使用一个能贯穿始终的模型，这样的模型整体性会显得特别好，在思维导图中能够有更好的展示。

问题 4 针对不同类别的玻璃文物样品，分析其化学成分之间的关联关系，并比较不同类别之间的化学成分关联关系的差异性。

对于问题四，我们可以使用贯穿问题一三的多元线性回归模型进行分析化学成分相关性，如果大家感觉这一个模型过于单一，大家也可以直接使用一些较为高级的关联性分析，比如我在作品中给大家分享的灰色关联分析等。也可以直接使用的。

稍后会为大家，一一解答疑问，预计明天上午会发布半成品论文，以及我的部分计算结果。

表单 1 玻璃文物的基本信息

表单 2 已分类玻璃文物的化学成分比例，其中

(1) 文物采样点为该编号文物表面某部位的随机采样，其风化属性与附件表单 1 中相应文物一致。

(2) 部位 1 和部位 2 是文物造型上不同的两个部位，其成分与含量可能存在差异。

(3) 未风化点是风化文物表面未风化区域内的点。

(4) 严重风化点取自风化层。

表单 3 未分类玻璃文物的化学成分比例

最后预祝大家比赛顺利，我们顶峰相见