蓝桥杯 --- 数学与简单DP

Posted 2023-04-09 在人间负债^

蓝桥杯 --- 数学与简单DP

• 数学
• • 1205. 买不到的数目
  • 1211. 蚂蚁感冒
  • 1216. 饮料换购
• 简单DP
• • 2. 01背包问题
  • 1015. 摘花生
  • 895. 最长上升子序列

数学

1205. 买不到的数目

小明开了一家糖果店。

他别出心裁：把水果糖包成4颗一包和7颗一包的两种。

糖果不能拆包卖。

小朋友来买糖的时候，他就用这两种包装来组合。

当然有些糖果数目是无法组合出来的，比如要买 10 颗糖。

你可以用计算机测试一下，在这种包装情况下，最大不能买到的数量是17。

大于17的任何数字都可以用4和7组合出来。

本题的要求就是在已知两个包装的数量时，求最大不能组合出的数字。

输入格式
两个正整数 n,m，表示每种包装中糖的颗数。

输出格式
一个正整数，表示最大不能买到的糖数。

数据范围

2≤n,m≤1000， 保证数据一定有解。

输入样例：

4 7

输出样例：

17

解题思路
裴蜀定理

#include<iostream>

using namespace std;

int main() 
	
	int n, m;
	cin >> n >> m;
	cout << (n - 1) * (m - 1) - 1 << endl;
	
 

1211. 蚂蚁感冒

长 100 厘米的细长直杆子上有 n 只蚂蚁。

它们的头有的朝左，有的朝右。

每只蚂蚁都只能沿着杆子向前爬，速度是 1 厘米/秒。

当两只蚂蚁碰面时，它们会同时掉头往相反的方向爬行。

这些蚂蚁中，有 1 只蚂蚁感冒了。

并且在和其它蚂蚁碰面时，会把感冒传染给碰到的蚂蚁。

请你计算，当所有蚂蚁都爬离杆子时，有多少只蚂蚁患上了感冒。

输入格式
第一行输入一个整数 n, 表示蚂蚁的总数。

接着的一行是 n 个用空格分开的整数 Xi, Xi 的绝对值表示蚂蚁离开杆子左边端点的距离。

正值表示头朝右，负值表示头朝左，数据中不会出现 0 值，也不会出现两只蚂蚁占用同一位置。

其中，第一个数据代表的蚂蚁感冒了。

输出格式
输出1个整数，表示最后感冒蚂蚁的数目。

数据范围

1<n<50 , 0<|Xi|<100

输入样例1：

3
5 -2 8

输出样例1：

1

输入样例2：

5
-10 8 -20 12 25

输出样例2：

3

解题思路
首先我们必须要明白两只蚂蚁相撞掉头可以看作时一只蚂蚁穿过了另一只蚂蚁，因为相撞之后两只蚂蚁都感冒了，掉不掉头其实无所谓，毕竟都感冒了，这样的话这题就简单多了。我们先不考虑特殊情况，先来看看一般情况：

第一只蚂蚁不管方向朝哪里，只要它右边的蚂蚁向左走就可能碰撞感染，同样，第一只蚂蚁左边的蚂蚁只要朝右边走也可能被感染，这样就很容易得到ans=right+left+1。这里left表示左边蚂蚁向右走的数量，right表示右边蚂蚁向左走的数量，1是指第一只蚂蚁本身。

还有一种特殊情况，就是当第一只蚂蚁向左走的时候，如果第一只蚂蚁左边没有向右爬行的蚂蚁，由于爬行速度相同，所以不管第一只蚂蚁右边有多少向左爬行的，其右边的蚂蚁永远不可能被感染。同理，当第一只蚂蚁向右走的时候，如果第一只蚂蚁右边没有向左爬行的蚂蚁，其左边也永远不可能感染。

#include<iostream>
#include<algorithm>

using namespace std;

int n;
int f[55];

int main() 
	
	cin >> n;
	int l = 0, r = 0;
	for(int i = 0; i <= n; i ++ ) cin >> f[i];
	for(int i = 0; i <= n; i ++ ) 
		if(abs(f[i]) < abs(f[0]) && f[i] > 0) l ++ ;
		if(abs(f[i]) > abs(f[0]) && f[i] < 0) r ++ ;
	
	if(f[0] > 0) 
		if(r > 0) cout << l + r + 1 << endl;
		else cout << 1 << endl;
	
	else 
		if(l > 0) cout << l + r + 1 << endl;
		else cout << 1 << endl;
	
	
	return 0;
	

1216. 饮料换购

乐羊羊饮料厂正在举办一次促销优惠活动。乐羊羊C型饮料，凭3个瓶盖可以再换一瓶C型饮料，并且可以一直循环下去(但不允许暂借或赊账)。

请你计算一下，如果小明不浪费瓶盖，尽量地参加活动，那么，对于他初始买入的 n 瓶饮料，最后他一共能喝到多少瓶饮料。

输入格式
输入一个整数 n,表示初始买入的饮料数量。

输出格式
输出一个整数，表示一共能够喝到的饮料数量。

数据范围

0<n<10000

输入样例：

100

输出样例：

149

解题思路
纯模拟…

#include<iostream>

using namespace std;

int n;

int main() 
	
	cin >> n;
	
	int pre = n / 3 + n % 3;
	int ans = n / 3;
	while(pre >= 3) 
		ans += pre / 3;
		pre = pre / 3 + pre % 3;
	
	
	cout << n + ans << endl;
	
	return 0;
	

简单DP

2. 01背包问题

有 N 件物品和一个容量是 V 的背包。每件物品只能使用一次。

第 i 件物品的体积是 vi，价值是 wi。

求解将哪些物品装入背包，可使这些物品的总体积不超过背包容量，且总价值最大。
输出最大价值。

输入格式
第一行两个整数，N，V，用空格隔开，分别表示物品数量和背包容积。

接下来有 N 行，每行两个整数 vi,wi，用空格隔开，分别表示第 i 件物品的体积和价值。

输出格式
输出一个整数，表示最大价值。

数据范围

0<N,V≤1000

0<vi,wi≤1000

输入样例

4 5
1 2
2 4
3 4
4 5

输出样例：

8

解题思路

//f[i][j]表示只选前i个物品（并不是前i个都选），总体积是j，总价值最大是多少（注意是最大，每次迭代的时候都是取的最大值） 
//对于第i件物品有两种选择：1.选第i件物品，2.不选第i件物品
//选第i件：f[i][j] = f[i - 1][j - v[i]]
//不选第i件：f[i][j] = f[i - 1][j]
//最后f[i][j] = max(1, 2) 
//result=max(f[n][0-j]) 


#include<iostream>

using namespace std;

const int N = 1010;

int n, m;
int v[N], w[N];
int f[N][N];

int main() 
	
	cin >> n >> m;
	for(int i = 1; i <= n; i ++ ) cin >> v[i] >> w[i];
	for(int i = 1; i <= n; i ++ ) 
		for(int j = 0; j <= m; j ++ ) 
			f[i][j] = f[i - 1][j];
			if(j >= v[i]) f[i][j] = max(f[i - 1][j], f[i - 1][j - v[i]] + w[i]);
		
	
	
	int ans = 0;
	for(int i = 0; i <= m; i ++ ) 
		ans = max(ans, f[n][i]);
	
	cout << ans << endl;
	
	return 0;

优化成一维

#include<iostream>

using namespace std;

const int N = 1010;

int n, m;
int v[N], w[N];
int f[N];

int main() 
	
	cin >> n >> m;
	for(int i = 1; i <= n; i ++ ) cin >> v[i] >> w[i];
	for(int i = 1; i <= n; i ++ ) 
		for(int j = m; j >= v[i]; j -- ) 
			f[j] = max(f[j], f[j - v[i]] + w[i]);
		
	
	
	int ans = 0;
	for(int i = 0; i <= m; i ++ ) 
		ans = max(ans, f[i]);
	
	cout << ans << endl;
	
	return 0;

1015. 摘花生

Hello Kitty想摘点花生送给她喜欢的米老鼠。

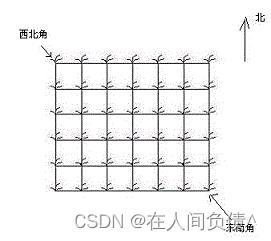
她来到一片有网格状道路的矩形花生地(如下图)，从西北角进去，东南角出来。

地里每个道路的交叉点上都有种着一株花生苗，上面有若干颗花生，经过一株花生苗就能摘走该它上面所有的花生。

Hello Kitty只能向东或向南走，不能向西或向北走。

问Hello Kitty最多能够摘到多少颗花生。

输入格式
第一行是一个整数T，代表一共有多少组数据。

接下来是T组数据。

每组数据的第一行是两个整数，分别代表花生苗的行数R和列数 C。

每组数据的接下来R行数据，从北向南依次描述每行花生苗的情况。每行数据有C个整数，按从西向东的顺序描述了该行每株花生苗上的花生数目M。

输出格式
对每组输入数据，输出一行，内容为Hello Kitty能摘到得最多的花生颗数。

数据范围

1≤T≤100,
1≤R,C≤100,
0≤M≤1000

输入样例：

2
2 2
1 1
3 4
2 3
2 3 4
1 6 5

输出样例：

8
16

解题代码

1. 状态表示
   集合：定义 f[i][j] 为从 ( 1 , 1 ) 到 ( i , j ) 的所有方案的集合
   属性：最大值
2. 状态转移
   ( i , j ) 从 ( i - 1 , j ) 转移过来
   ( i , j ) 从 ( i , j - 1 ) 转移过来
3. 空间压缩
   f[i][j] 主需要用到这一层和上一层的 f 元素，所以可以压缩成滚动数组。再次之上，还可以直接压缩成一维数组。

#include<iostream>
#include<algorithm>
#include<cstring>
#include<cmath>
#include<vector>
#include<stack>
#include<queue>
#include<sstream>
#include<set>
#include<map>

#define x first
#define y second

using namespace std;
typedef long long ll;
typedef pair<int, int> PII;
const int N = 110;
const int MOD = 1000000007;
const int INF = 0x3f3f3f3f;

int gcd(int a, int b)return b ? gcd(b, a % b) : a;

int g[N][N];
int f[N][N];

int main()

	int t;
	cin >> t;
	while(t -- ) 
		int r, c;
		cin >> r >> c;
		for(int i = 1; i <= r; i ++ ) 
			for(int j = 1; j <= c; j ++ ) 
				cin >> g[i][j];
			
		
		for(int i = 1; i <= r; i ++ ) 
			for(int j = 1; j <= c; j ++ ) 
				f[i][j] = max(f[i - 1][j] + g[i][j], f[i][j - 1] + g[i][j]);
			
		
		int ans = 0;
		for(int i = 1; i <= r; i ++ ) 
			for(int j = 1; j <= c; j ++ ) 
				ans = max(ans, f[i][j])
			
		
		cout << ans << endl;
	

	return 0;

895. 最长上升子序列

给定一个长度为 N 的数列，求数值严格单调递增的子序列的长度最长是多少。

输入格式
第一行包含整数 N。

第二行包含 N 个整数，表示完整序列。

输出格式
输出一个整数，表示最大长度。

数据范围

1≤N≤1000，
−10⁹≤数列中的数≤10⁹

输入样例：

7
3 1 2 1 8 5 6

输出样例：

4

解题思路

1. 状态表示
   f[i] 表示从第一个数字开始，以 a[i] 结尾的最大上升的序列
2. 状态计算
   f[i] = max( f[i] , f[j] + 1 )
   有一个边界，若前面没有比 a[i] 小的，f[i] 为 1（自己开头，自己结尾）
3. 结果
   在 f[i] 中找出最大值

#include<iostream>
#include<algorithm>
#include<cstring>
#include<cmath>
#include<vector>
#include<stack>
#include<queue>
#include<sstream>
#include<set>
#include<map>

#define x first
#define y second

using namespace std;
typedef long long ll;
typedef pair<int, int> PII;
const int N = 1010;
const int MOD = 1000000007;
const int INF = 0x3f3f3f3f;

int gcd(int a, int b)return b ? gcd(b, a % b) : a;

int a[N];
int f[N];

int main()

	int n;
	cin >> n;
	for(int i = 1; i <= n; i ++ ) cin >> a[i];
	int ans = 0;
	for(int i = 1; i <= n; i ++ ) 
		f[i] = 1;
		for(int j = 1; j < i; j ++ ) 
			if(a[i] > a[j]) 
				f[i] = max(f[i], f[j] + 1);
			
		
	
	for(int i = 1; i <= n; i ++ ) 
	    ans = max(ans, f[i]);
	
	cout << ans << endl;

	return 0;

蓝桥杯国赛 对局匹配（DP）

蓝桥杯国赛 对局匹配（DP）

题目描述

小明喜欢在一个围棋网站上找别人在线对弈。这个网站上所有注册用户都有一个积分，代表他的围棋水平。

小明发现网站的自动对局系统在匹配对手时，只会将积分差恰好是 K 的两名用户匹配在一起。如果两人分差小于或大于 KK，系统都不会将他们匹配。

现在小明知道这个网站总共有 N名用户，以及他们的积分分别是 $A_1,A_2,\cdots A_N$

小明想了解最多可能有多少名用户同时在线寻找对手，但是系统却一场对局都匹配不起来(任意两名用户积分差不等于 K)？

输入描述

输入描述

第一行包含两个个整数 N,K。

第二行包含 NN 个整数$A_1,A_2,\cdots A_N$

其中，$1\le N\le 10^5,0\le Ai\le 10^5,0\le K\le 10^5$

输出描述

输出一个整数，代表答案。

输入输出样例

示例

输入

10 0
1 4 2 8 5 7 1 4 2 8

输出

6

思路

这道题有点难，我也是参考了众多博客终于大概搞明白了，这道题简单来说就是一个动态规划的问题，这里是差值只要是k就不能同时选，所以会将差值为k的划分为一组，然后每一组进行动态规划就可以了
$$dp[i]=max(dp[i-k],dp[i-2k]+a[i])$$
首先最简单的就是k=0的情况，对于k=0的情况来说，我们只需要得到不同积分的数就可以了

而对于k不为0的情况，需要详细分析

• 首先把n个元素按照分数相差为k1的用户分为一组，例如第一组就是0,k,2k,3k…，第二组就是1,k+1,2k+1…等，这样每个组的用户不可能和其他组的用户匹配成功，因为他们之间的差不可能为k

• 其二目标就是在每一个分组里面选取尽量多的用户，这一部分我们就可以用动态规划来求解，选取尽可能多的人数。dp[i]表示前i个积分能获得的最大用户数（不能匹配的）

  • 如果 j 不上线，则 j-k 是会上线，所以人数就是j-k的人数
  • 如果 j 上线， 则不影响 j-2*k，所以j-2k可以上线，所以最后是j的人数j-2k的人数

• 最后就可以得到我们的动态规划的方程，最后进行求解
  $$dp[i]=max(dp[i-k],dp[i-2k]+a[i])$$

代码

n,k = map(int,input().split())

a = list(map(int,input().split()))
maxa = max(a)
from collections import Counter

c = Counter(a)
if k == 0:
    print(len(c))
else:
    # dp[i]表示前i个积分能获得的最大用户数（不能匹配的）
    dp = [0]*(maxa+1)
    ans = 0
    for i in range(0,k):
        maxindex = 0
        # 这里相当于分组，分为k,2k,3k....
        # 希望在每一分组中选择尽可能多的客户
        for j in range(i,maxa+1,k):
            if j - 2*k >= 0:
                # 如果 j 不上线，则j-k上线
                # 如果 j 上线， 则不影响j-2*k，所以j-2k可以上线
                dp[j] = max(dp[j-2*k]+c[j],dp[j-k])
            elif j - k >= 0:
                dp[j] = max(dp[j-k],c[j])
            else:
                dp[j] = c[j]
            maxindex = j
        ans += dp[maxindex]
    print(ans)