数据加密标准DES详细过程总结代码（自运行可实现）

Posted 2023-04-08 陈如初

1、公开征集密码算法标准的主要要求

• 算法必须是安全的：具有加密保护信息安全的能力
• 算法必须是公开的：有完整的算法说明、容易理解、能为所有用户使用
• 能够经济、有效的硬件实现：性能好
• 能够得到批准：合法
• 可出口：大众化

2、DES概述

• 分组加密算法：明文和密文为64位分组长度
• 对称算法：加密和解密除密钥编排不同之外，使用的是同一算法
• 密钥长度：56位，但存在弱密钥，容易避开
• 混乱（S盒）和扩散（P盒）组合，每个组合先代换后置换，共16轮
• 只使用标准的算数和逻辑运算，易于实现。
• 商业密码、现代密码学的标志。

3、DES的实现

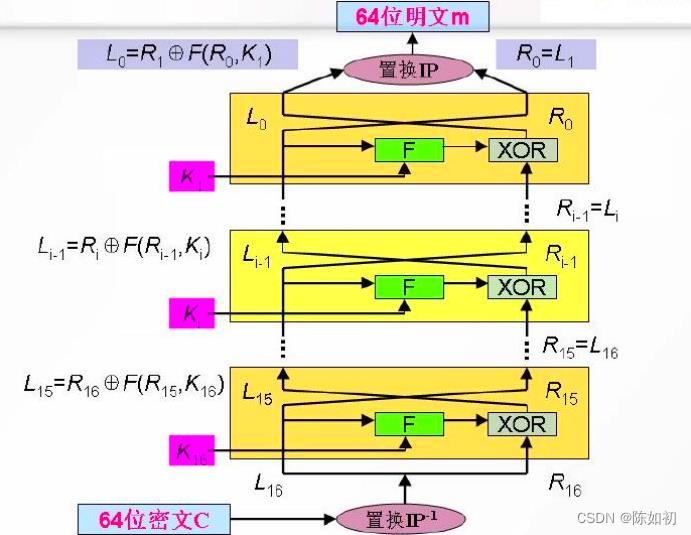
（1）、DES算法的整体结构----Feistel结构

*细节流程图

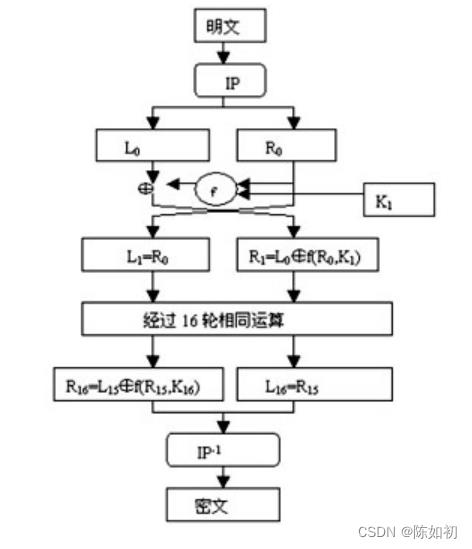
• Feistel提出利用乘积密码可获得简单的代换密码
• Feistel还提出了实现代换和置换的方法
• 很多分组密码的结构从本质上说都是基于一个称
  为Feistel网络的结构

（2）、第一步：密钥的编排 （为加密做准备）

1. 密钥生成：

• 从用户处取得一个64位(本文均指二进制位))长的密码口令key ，key=k1k2k3…k63k64。
• 去除64位密码中作为奇偶校验位的第8、16、24、32、40、48、56、64位，剩下的56位作为有效输入密钥。

2. 等分密钥：

3. 输入密钥位序/ A位序对照表
   
   输入密钥位序/ B位序对照表
   
   这样 key=k1k2k3…k55k56 形成了A、B两部分：
   A = k57k49k41…k44k36
   B=k65k55k47…k12k4

4. 密钥移位
   DES算法的密钥是经过16次迭代（循环左移）得到一组密钥的
   
   Ps：生成的A、B视为迭代的起始密钥，上表显示每一次迭代时密钥循环左移的位数。 比如在第1次迭代时密钥循环左移1位，第3次迭代时密钥循环左移2位…第9次迭代时密钥循环左移1位，第14次迭代时密钥循环左移2位。

5. 迭代并乘积合并得到密钥C

• 第一次迭代：
  A(1) =(1) A

• 第i次迭代：
  A(i) =(i) A(i-1)
  B(i) =(i) B(i-1)

• 第i次迭代生成的两个28位长的密钥并乘积得到56位密钥C(i)=A（i）B(i)=A(i)1…A(i)28B(i)1…B(i)28

6. 对密钥C进行加密，故产生加密密钥K

• 56位密钥C的位序与加密密钥K的位序对照表
  
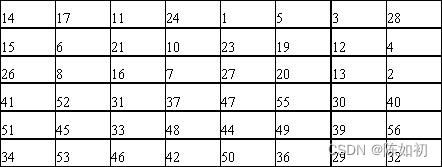
  Ps：k的第一位为56位密钥的第14位，k的第2位为56位密钥的第17位，依此类推，k的最后一位第48位是56位密钥的第32位。 这样，就生成了一个48位使用密钥：K=k(i)1k(i)2…k(i)48

7. DES算法密钥生成需要进行16次迭代，在完成16次迭代前，循环执行上述第4步和第5步，最终形成16套加密密钥：key[0]，key[1]，key[2]，…。key[14]，key[15]。即以下第二步

（3）、第二步：16轮迭代

按下述规则进行16次迭代：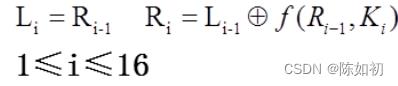
Ps1：这里的 “＋” 是对应比特的模加2，f 是一个函数（轮函数）。
Ps2：16个长度为48比特的子密钥ki(1≤i≤16)是由密钥k经密钥编排函数计算出来的。
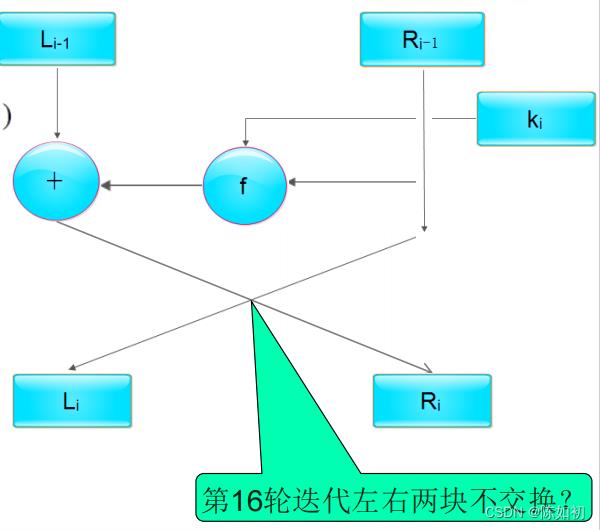Ps3：第16轮迭代左右数值不做交换

（4）、第三步：IP置换（加密）

给定明文，通过一个固定的初始置换IP来重排输入明文块P中的比特，得到比特串P0=IP（P）=L0R0，这 里L0和R0分别是P0的前32比特和后32比特
Ps：利用乘积密码可获得简单的代换密码

（5）、第四步：IP逆置（解密）

对比特串R16L16使用逆置换IP-1得到密文C，即
C=IP-1 (R16L16)。

***以上为含图简介，为了更好理解这个过程，避免看很多头疼的流程图，我们用文字叙述的方式来简述加密解密的详细过程，即以上（4）、（5）为数据加密解密的简介，以下为具体过程：

1.总体过程
DES对64位明文分组进行操作。通过一个初始置换，将明文分组分成左半部分和右半部分，各32位长。
然后进行16轮完全相同的运算，这些运算被称为函数 f，在运算过程中数据与密钥结合。经过16轮
后，左、右半部分合在一起经过一个末置换（初始置换的逆置换），算法就完成了。
在每一轮中，密钥位移位，然后再从密钥的56位中选出48位。通过一个扩展置换将数据的右半部分
扩展成48位，并通过一个异或操作与48位密钥结合，通过 8个S盒将这48位替代成新的32位数据，再
将其置换一次。这四步运算构成了函数f。然后，通过另一个异或运算，函数f的输出与左半部分结合，
其结果即成 为新的左半部分。将该操作重复16次，便实现了DES的16轮运算。
假设Bi是第i次迭代的结果，Li和Ri是Bi的左半部分和右半部分，Ki是第i轮的48位密钥，且f是实现
代替、置换及密钥异或等运算的函数，那么每一轮就是：
 Li=Ri-1
 Ri=Li-1⊕f(Ri-1,Ki)

2、初始置换
初始置换在第一轮运算之前进行，对输入分组实施如下表所示的变换。初始置换把明文的第58位换到第1位的位置，把第50位换到第2位的位置，把第42位换到第3位的位置，以此类推。
58, 50, 42, 34, 26, 18, 10, 2, 60, 52, 44, 36, 28, 20, 12, 4
62, 54, 46, 38, 30, 22, 14, 6, 64, 56, 48, 40, 32, 24, 16, 8
57, 49, 41, 33, 25, 17, 9, 1, 59, 51, 43, 35, 27, 19, 11, 3
61, 53, 45, 37, 29, 21, 13, 5, 63, 55, 47, 39, 31, 23, 15, 7
初始置换和对应的末置换并不影响DES的安全性，它们的主要目的是为了更容易地将明文和密文数据以字节大小放入DES芯片中。

3、密钥置换
由于不考虑每个字节的第8位，DES的密钥由64位减至56位，每个字节第8位作为奇偶校验以确保密钥不发生错误。如下表所示：
57, 49, 41, 33, 25, 17, 9, 1, 58, 50, 42, 34, 26, 18
10, 2, 59, 51, 43, 35, 27, 19, 11, 3, 60, 52, 44, 36
63, 55, 47, 39, 31, 23, 15, 7, 62, 54, 46, 38, 30, 22
14, 6, 61, 53, 45, 37, 29, 21, 13, 5, 28, 20, 12, 4
在DES的每一轮中，从56位密钥产生出不同的48位子密钥(subkey)，这些子密钥是这样确定的：
首先，56位密钥被分成两部分，每部分28位。
然后，根据轮数，这两部分分别循环左移1位或2位。每轮移动的位数如下表：
轮 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
位数 1 1 2 2 2 2 2 2 1 2 2 2 2 2 2 1
移动后，就从56位中选出48位。这个运算既置换了每位的顺序，也选择了子密钥，被称为压缩置换(compression permutation)。下表即定义了压缩置换：
14, 17, 11, 24, 1, 5, 3, 28, 15, 6, 21, 10
23, 19, 12, 4, 26, 8, 16, 7, 27, 20, 13, 2
41, 52, 31, 37, 47, 55, 30, 40, 51, 45, 33, 48
44, 49, 39, 56, 34, 53, 46, 42, 50, 36, 29, 32
可以看出，第33位的那一位在输出时移到了第35位，而处于第18位的那一位被忽略了。

4、扩展置换 （轮函数f的一部分）
这个运算将数据的右半部分从32位扩展到48位。这个操作两方面的目的：它产生了与密钥同长度的数据以进行异或运算；它提供了更长的结果，使得在替代运算中能进行压缩。
对每个4位输入分组，第1位和第4位分别表示输出分组中的两位，而第2位和第3位分别表示输出分组中的一位，下表给出了哪一输出位对应哪一输入位：
32, 1, 2, 3, 4, 5, 4, 5, 6, 7, 8, 9
8, 9, 10, 11, 12, 13, 12, 13, 14, 15, 16, 17
16, 17, 18, 19, 20, 21, 20, 21, 22, 23, 24, 25
24, 25, 26, 27, 28, 29, 28, 29, 30, 31, 32, 1
处于输入分组中第3位的位置移到了输出分组中的第4位，而输入分组的第21位则移到了输出分组的第30位和第32位。尽管输出分组大于输入分组，但每一个输入分组产生唯一的输出分组。

5、S盒代替 （轮函数f的一部分）
压 缩后的密钥与扩展分组异或以后，将48位的结果送入，进行代替运算。替代由8个S盒完成，每一个S盒都由6位输入，4位输出，且这8个S盒是不同的。48 位的输入被分为8个6位的分组，每一个分组对应一个S盒代替操作：分组1由S盒1操作，分组2由S盒2操作，等等。如下图所示：
每一个S盒是一个4行、16列的表。盒中的每一项都是一个4位的数。S盒的6个位输入确定了其对应的输出在哪一行哪一列。下表列出所有8个S盒：
S盒1:
14, 4, 13, 1, 2, 15, 11, 8, 3, 10, 6, 12, 5, 9, 0, 7
0, 15, 7, 4, 14, 2, 13, 1, 10, 6, 12, 11, 9, 5, 3, 8
4, 1, 14, 8, 13, 6, 2, 11, 15, 12, 9, 7, 3, 10, 5, 0
15, 12, 8, 2, 4, 9, 1, 7, 5, 11, 3, 14, 10, 0, 6, 13
S盒2:
15, 1, 8, 14, 6, 11, 3, 4, 9, 7, 2, 13, 12, 0, 5, 10
3, 13, 4, 7, 15, 2, 8, 14, 12, 0, 1, 10, 6, 9, 11, 5
0, 14, 7, 11, 10, 4, 13, 1, 5, 8, 12, 6, 9, 3, 2, 15
13, 8, 10, 1, 3, 15, 4, 2, 11, 6, 7, 12, 0, 5, 14, 9
S盒3:
10, 0, 9, 14, 6, 3, 15, 5, 1, 13, 12, 7, 11, 4, 2, 8
13, 7, 0, 9, 3, 4, 6, 10, 2, 8, 5, 14, 12, 11, 15, 1
13, 6, 4, 9, 8, 15, 3, 0, 11, 1, 2, 12, 5, 10, 14, 7
1, 10, 13, 0, 6, 9, 8, 7, 4, 15, 14, 3, 11, 5, 2, 12
S盒4:
7, 13, 14, 3, 0, 6, 9, 10, 1, 2, 8, 5 ,11, 12, 4, 15
13, 8, 11, 5, 6, 15, 0, 3, 4, 7, 2, 12, 1, 10, 14, 9
10, 6, 9, 0, 12, 11, 7, 13, 15, 1, 3, 14, 5, 2, 8, 4
3, 15, 0, 6, 10, 1, 13, 8, 9, 4, 5, 11, 12, 7, 2, 14
S盒5:
2, 12, 4, 1, 7, 10, 11, 6, 8, 5, 3, 15, 13, 0, 14, 9
14, 11, 2, 12, 4, 7, 13, 1, 5, 0, 15, 10, 3, 9, 8, 6
4, 2, 1, 11, 10, 13, 7, 8, 15, 9, 12, 5, 6, 3, 0, 14
11, 8, 12, 7, 1, 14, 2, 13, 6, 15, 0, 9, 10, 4, 5, 3
S盒6:
12, 1, 10, 15, 9, 2, 6, 8, 0, 13, 3, 4, 14, 7, 5, 11
10, 15, 4, 2, 7, 12, 9, 5, 6, 1, 13, 14, 0, 11, 3, 8
9, 14, 15, 5, 2, 8, 12, 3, 7, 0, 4, 10, 1, 13, 11, 6
4, 3, 2, 12, 9, 5, 15, 10, 11, 14, 1, 7, 6, 0, 8, 13
S盒7:
4, 11, 2, 14, 15, 0, 8, 13, 3, 12, 9, 7, 5, 10, 6, 1
13, 0, 11, 7, 4, 9, 1, 10, 14, 3, 5, 12, 2, 15, 8, 6
1, 4, 11, 13, 12, 3, 7, 14, 10, 15, 6, 8, 0, 5, 9, 2
6, 11, 13, 8, 1, 4, 10, 7, 9, 5, 0, 15, 14, 2, 3, 12
S盒8:
13, 2, 8, 4, 6, 15, 11, 1, 10, 9, 3, 14, 5, 0, 12, 7
1, 15, 13, 8, 10, 3, 7, 4, 12, 5, 6, 11, 0, 14, 9, 2
7, 11, 4, 1, 9, 12, 14, 2, 0, 6, 10, 13, 15, 3, 5, 8
2, 1, 14, 7, 4, 10, 8, 13, 15, 12, 9, 0, 3, 5, 6, 11
假定将S盒的6位的输入标记位b1、b2、b3、b4、b5、b6。则b1和b6组合构成了一个2位数，从0到3，它对应着表的一行。从b2到b5构成了一个4位数，从0到15，对应着表中的一列。
例如，假设第6个S盒的输入为110011，第1位和第6位组合形成了11，对应着第6个S盒的第三行，中间4位组合形成了1001，它对应着同一个S盒的第9列，S盒6在第三行第9列的数是14，则用值1110来代替110011。
这是DES算法的关键步骤，所有其他的运算都是线性的，易于分析，而S盒是非线性的，它比DES的其他任何一步提供了更好的安全性。
这个代替过程的结果是8个4位的分组，他们重新合在一起形成了一个32位的分组。

6、P盒置换 （轮函数f的一部分）
S盒代替运算的32位输出依照P盒进行置换。该置换把每输入位映射到输出位，任一位不能被映射两次，也不能被略去，下表给出了每位移至的位置：
16, 7, 20, 21, 29, 12, 28, 17, 1, 15, 23, 26, 5, 18, 31, 10
2, 8, 24, 14, 32, 27, 3, 9, 19, 13, 30, 6, 22, 11, 4, 25
第21位移到了第4位，同时第4位移到了第31位。
最后，将P盒置换的结果与最初的64位分组的左半部分异或，然后左、右半部分交换，接着开始另一轮。

7、末置换 （轮函数f的一部分）
末置换是初始置换的逆过程。DES在最后一轮后，左半部分和右半部分并未交换，而是将两部分并在一起形成一个分组作为末置换的输入，该置换如下表如示：
40, 8, 48, 16, 56, 24, 64, 32, 39, 7, 47, 15, 55, 23, 63, 31
38, 6, 46, 14, 54, 22, 62, 30, 37, 5, 45, 13, 53, 21, 61, 29
36, 4, 44, 12, 52, 20, 60, 28, 35, 3, 43, 11, 51, 19, 59, 27
34, 2, 42, 10, 50, 18, 58, 26, 33, 1, 41, 9, 49, 17, 57, 25

8、DES的解密
DES使得用相同的函数来加密或解密每个分组成为可能，二者唯一的不同就是密钥的次序相反。

4、S盒设计的重要性

& DES的核心是S盒，除此之外的计算是线性的
& S盒作为该密码体制的非线性组件对安全性至
关重要
& S盒的设计准则：
1、 具有良好的非线性（输出的每一个比特与全部
输入比特有关）
2、每一行包括所有16种4位二进制
3、两个输入相差1bit时，输出相差2bit
4、 如果两个输入刚好在中间两个比特上不同，则
输出至少有两个比特不同
5、 如果两个输入前两位不同而最后两位相同，则
输出一定不同
6、 相差6bit的输入共有32对，在这32对中有不超
过8对的输出相同

5、DES缺陷

 密钥分配问题：通信双方要进行加密通信，
需要通过秘密的安全信道协商加密密钥，而
这种安全信道可能很难实现

 密钥管理问题：在有多个用户的网络中，任
何两个用户之间都需要有共享的秘密钥，当
网络中的用户n很大时，需要管理的密钥数目
非常大n(n-1)/2

 互补性，是由算法中的两次异或运算的配置所决定的。两次异或运算一次在S盒之前，一次在P盒置换之后。

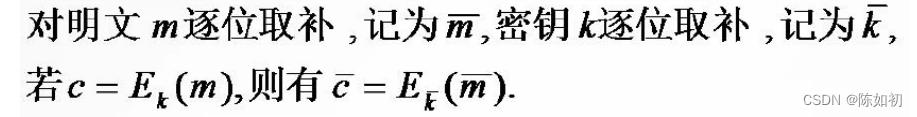
若对DES输入的明文和密钥同时取补，则选择扩展运算E的输出和子密钥产生器的输出也都取补，因
而经异或运算后的输出和明文及密钥未取补时的输出一样，这使得到达S盒的输入数据未变，其输出自然也不会变，但经第二个异或运算时，由于左边的数据已取补，因而输出也就取补了

互补性会使DES在选择明文攻击下所需的工作量减半

 弱密钥和半弱密钥

1、弱密钥

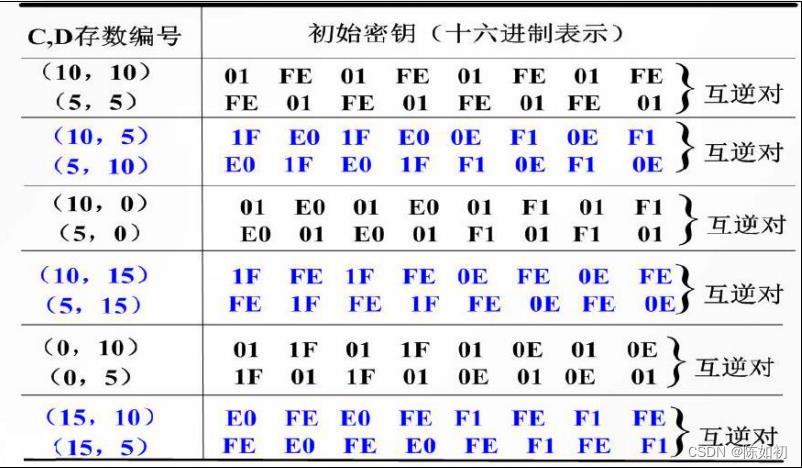
• 如果给定初始密钥k，经子密钥产生器产生的各个子密钥都相同，即有kl=k2=…=k16，则称给定的初始密钥k为弱密钥。
• 若 k 为
  弱 密 钥 ， 则 对 任 意 的 64bit 信 息 有 ：Ek(Ek(m))=m和Dk(Dk(m))=m
• 弱密钥的构造由子密钥产生器中寄存器C和D中的存 数在循环移位下出现重复图样决定的（C和D中的存 数为全0或全1）共有4个（十六进制）：
  

2、半弱密钥

• 若给定初始密钥k，产生的16个子密钥只有两种，且每种都出现8次，则称k为半弱密钥。

• 半弱密钥的特点是成对出现， 且具有下述性质：
  若k1和k2为一对弱密钥，m为明文组，则有：Ek2(Ek1(m))=Ek1(Ek2(m))=m此外，还有四分之一弱密钥等。

• DES的密钥中，弱密钥的比例非常小，而且极易避开，因此，弱密钥的存在对DES的安全性威胁不大。
  

 密钥搜索

DES的强度：56比特的密钥长度：

• 如果每秒搜索106个密钥，大约需要100年。
• 采用并行技术，97年10万美金的机器(5760个搜索5xl07芯片) 1.5天用穷举法找到DES密钥。
• 密钥分割的方法：利用Internet的分布式计算能力， 组织志愿者连接了100000台计算机系统，在22小时15分钟完成DES算法的攻击。

 差分分析和线性分析

• 差分分析是一种攻击迭代密码体制的选择明文攻击 方法
• 与一般统计分析法的不同之处是，它不是直接分析密文或密钥和明文的统计相关性，而是分析一对给定明文的异或（称为差分）与对应密文对的 异或之间的统计相关性。
• 差分分析的基本思想是在要攻击的迭代密码系统中找出某些高概率的明文差分和密文差分对来推算密钥。 利用此法攻击DES，需要用247个选择明文和247次加密运算，比穷举搜索的工作量大大减少。

 线性分析（实际上不可行）

• 基本思想是：以最佳的线性函数逼近DES的非线 性变换S盒，这是一种已知明文攻击方法，可以在 有243个已知明文的情况下破译DES。
• 虽然获得已知明文比选择明文更容易，但线性分析作为一种攻击 手段在实际上仍然不可行

6、多重DES

1. 为了提高DES的安全性能，并充分利用有关DES的现有软件和硬件资源，可以使用多重DES。
2. 多重DES就是使用多个密钥利用DES对明文进行多次加密。
3. 使用多重DES可以增加密钥量，从而大大提高抵抗密钥的穷举搜索攻击的能力。
4. 已经证明多重DES并不等价于多次使用一个56位密钥的单重DES。
5. 二重DES/三重DES
6. 多重DES的四种模式：
   

7、代码

#include <stdio.h> 
#include <stdlib.h> 
#include <string.h> 
#include <openssl/des.h> 
#pragma comment(lib,"libssl.lib")
#pragma comment(lib,"libcrypto.lib")
using namespace std;
/************************************************************************
** 本例采用：
** 3des-ecb加密方式；
** 24位密钥，不足24位的右补0x00；
** 加密内容8位补齐，补齐方式为：少1位补一个0x01,少2位补两个0x02,...
** 本身已8位对齐的，后面补八个0x08。
************************************************************************/
int main(void)

    int docontinue = 1;
    char data[20] = "hello world!"; /* 明文 */
    int data_len;
    int data_rest;
    unsigned char ch;
    unsigned char* src = NULL; /* 补齐后的明文 */
    unsigned char* dst = NULL; /* 解密后的明文 */
    int len;
    unsigned char tmp[8];
    unsigned char in[8];
    unsigned char out[8];
    char k[100] = "01234567899876543210"; /* 原始密钥 */
    int key_len;
#define LEN_OF_KEY 24 
    unsigned char key[LEN_OF_KEY]; /* 补齐后的密钥 */
    unsigned char block_key[9];
    DES_key_schedule ks, ks2, ks3;
    /* 构造补齐后的密钥 */
    key_len = strlen(k);
    memcpy(key, k, key_len);
    memset(key + key_len, 0x00, LEN_OF_KEY - key_len);
    /* 分析补齐明文所需空间及补齐填充数据 */
    data_len = strlen(data);
    data_rest = data_len % 8;
    len = data_len + (8 - data_rest);
    ch = 8 - data_rest;
    src = (unsigned char*)malloc(len);
    dst = (unsigned char*)malloc(len);
    if (NULL == src || NULL == dst)
    
        docontinue = 0;
    
    if (docontinue)
    
        int count;
        int i;
        /* 构造补齐后的加密内容 */
        memset(src, 0, len);
        memcpy(src, data, data_len);
        memset(src + data_len, ch, 8 - data_rest);
        /* 密钥置换 */
        memset(block_key, 0, sizeof(block_key));
        memcpy(block_key, key + 0, 8);
        DES_set_key_unchecked((const_DES_cblock*)block_key, &ks);
        memcpy(block_key, key + 8, 8);
        DES_set_key_unchecked((const_DES_cblock*)block_key, &ks2);
        memcpy(block_key, key + 16, 8);
        DES_set_key_unchecked((const_DES_cblock*)block_key, &ks3);
        printf("before encrypt:\\n");
        for (i = 0; i < len; i++)
        
            printf("0x%.2X ", *(src + i));
        
        printf("\\n");
        /* 循环加密/解密，每8字节一次 */
        count = len / 8;
        for (i = 0; i < count; i++)
        
            memset(tmp, 0, 8);
            memset(in, 0, 8);
            memset(out, 0, 8);
            memcpy(tmp, src + 8 * i, 8);
            /* 加密 */
            DES_ecb3_encrypt((const_DES_cblock*)tmp, (DES_cblock*)in, &ks, &ks2, &ks3, DES_ENCRYPT);
            /* 解密 */
            DES_ecb3_encrypt((const_DES_cblock*)in, (DES_cblock*)out, &ks, &ks2, &ks3, DES_DECRYPT);
            /* 将解密的内容拷贝到解密后的明文 */
            memcpy(dst + 8 * i, out, 8);
        
        printf("after decrypt :\\n");
        for (i = 0; i < len; i++)
        
            printf("0x%.2X ", *(dst + i));
        
        printf("\\n");
    
    if (NULL != src)
    
        free(src);
        src = NULL;
    
    if (NULL != dst)
    
        free(dst);
        dst = NULL;
    
    return 0;

加密技术06-加密总结

参考技术A

对称密码是一种用相同的密钥进行加密和解密的技术，用于确保消息的机密性。在对称密码的算法方面，目前主要使用的是 AES。尽管对称密码能够确保消息的机密性，但需要解决将解密密钥配送给接受者的密钥配送问题。

主要算法

DES

数据加密标准（英语：Data Encryption Standard，缩写为 DES）是一种对称密钥加密块密码算法，1976年被美国联邦政府的国家标准局确定为联邦资料处理标准（FIPS），随后在国际上广泛流传开来。它基于使用56位密钥的对称算法。

DES现在已经不是一种安全的加密方法，主要因为它使用的56位密钥过短。

原理请参考： 加密技术01-对称加密-DES原理

3DES

三重数据加密算法（英语：Triple Data Encryption Algorithm，缩写为TDEA，Triple DEA），或称3DES（Triple DES），是一种对称密钥加密块密码，相当于是对每个数据块应用三次DES算法。由于计算机运算能力的增强，原版DES由于密钥长度过低容易被暴力破解；3DES即是设计用来提供一种相对简单的方法，即通过增加DES的密钥长度来避免类似的攻击，而不是设计一种全新的块密码算法。

注意：有3个独立密钥的3DES的密钥安全性为168位，但由于中途相遇攻击（知道明文和密文），它的有效安全性仅为112位。

3DES使用“密钥包”，其包含3个DES密钥，K1，K2和K3，均为56位（除去奇偶校验位）。

密文 = E k3 (D k2 (E k1 (明文)))

而解密则为其反过程：

明文 = D k3 (E k2 (D k1 (密文)))

AES

AES 全称 Advanced Encryption Standard（高级加密标准）。它的出现主要是为了取代 DES 加密算法的，因为 DES 算法的密钥长度是 56 位，因此算法的理论安全强度是 56 位。于是 1997 年 1 月 2 号，美国国家标准技术研究所宣布希望征集高级加密标准，用以取代 DES。AES 也得到了全世界很多密码工作者的响应，先后有很多人提交了自己设计的算法。最终有5个候选算法进入最后一轮：Rijndael，Serpent，Twofish，RC6 和 MARS。最终经过安全性分析、软硬件性能评估等严格的步骤，Rijndael 算法获胜。

AES 密码与分组密码 Rijndael 基本上完全一致，Rijndael 分组大小和密钥大小都可以为 128 位、192 位和 256 位。然而 AES 只要求分组大小为 128 位，因此只有分组长度为 128 位的 Rijndael 才称为 AES 算法。

本文 AES 默认是分组长度为 128 位的 Rijndael 算法

原理请参考： 加密技术02-对称加密-AES原理

算法对比

公钥密码是一种用不同的密钥进行加密和解密的技术，和对称密码一样用于确保消息的机密性。使用最广泛的一种公钥密码算法是 RAS。和对称密码相比，公钥密码的速度非常慢，因此一般都会和对称密码一起组成混合密码系统来使用。公钥密码能够解决对称密码中的密钥交换问题，但存在通过中间人攻击被伪装的风险，因此需要对带有数字签名的公钥进行认证。

公钥密码学的概念是为了解决对称密码学中最困难的两个问题而提出

应用场景

几个误解

主要算法

Diffie–Hellman 密钥交换

迪菲-赫尔曼密钥交换（英语：Diffie–Hellman key exchange，缩写为D-H） 是一种安全协议。它可以让双方在完全没有对方任何预先信息的条件下通过不安全信道创建起一个密钥。这个密钥可以在后续的通讯中作为对称密钥来加密通讯内容。公钥交换的概念最早由瑞夫·墨克（Ralph C. Merkle）提出，而这个密钥交换方法，由惠特菲尔德·迪菲（Bailey Whitfield Diffie）和马丁·赫尔曼（Martin Edward Hellman）在1976年发表，也是在公开文献中发布的第一个非对称方案。

Diffie–Hellman 算法的有效性是建立在计算离散对数很困难的基础上。简单地说，我们可如下定义离散对数。首先定义素数 p 的本原跟。素数 p 的本原根是一个整数，且其幂可以产生 1 到 p-1 之间所有整数，也就是说若 a 是素数 p 的本原根，则

a mod p, a 2 mod p,..., a p-1 mod p 各不相同，它是整数 1 到 p-1 的一个置换。

对任意整数 b 和素数 p 的本原跟 a，我们可以找到唯一的指数 i 使得

b ≡ a i (mod p) 其中 0 <= i <= p-1

其中 a, b, p 这些是公开的，i 是私有的，破解难度就是计算 i 的难度。

Elgamal

1985年，T.Elgamal 提出了一种基于离散对数的公开密钥体制，一种与 Diffie-Hellman 密钥分配体制密切相关。Elgamal 密码体系应用于一些技术标准中，如数字签名标准(DSS) 和 S/MIME 电子邮件标准。

基本原理就是利用 Diffie–Hellman 进行密钥交换，假设交换的密钥为 K，然后用 K 对要发送的消息 M，进行加密处理。

所以 Elgamal 的安全系数取决于 Diffie–Hellman 密钥交换。

另外 Elgamal 加密后消息发送的长度会增加一倍。

RSA

MIT 的罗纳德·李维斯特（Ron Rivest）、阿迪·萨莫尔（Adi Shamir）和伦纳德·阿德曼（Leonard Adleman）在 1977 年提出并于 1978 年首次发表的算法。RSA 是最早满足要求的公钥算法之一，自诞生日起就成为被广泛接受且被实现的通用的公钥加密方法。

RSA 算法的有效性主要依据是大数因式分解是很困难的。

原理请参考： 加密技术03-非对称加密-RSA原理

ECC

大多数使用公钥密码学进行加密和数字签名的产品和标准都使用 RSA 算法。我们知道，为了保证 RSA 使用的安全性，最近这些年来密钥的位数一直在增加，这对使用 RSA 的应用是很重的负担，对进行大量安全交易的电子商务更是如此。近来，出现的一种具有强大竞争力的椭圆曲线密码学（ECC）对 RSA 提出了挑战。在标准化过程中，如关于公钥密码学的 IEEE P1363 标准中，人们也已考虑了 ECC。

与 RSA 相比，ECC 的主要诱人之处在于，它可以使用比 RSA 短得多的密钥得到相同安全性，因此可以减少处理负荷。

ECC 比 RSA 或 Diffie-Hellman 原理复杂很多，本文就不多阐述了。

算法对比

公钥密码体制的应用

密码分析所需计算量（ NIST SP-800-57 ）

注：L=公钥的大小，N=私钥的大小

散列函数是一种将长消息转换为短散列值的技术，用于确保消息的完整性。在散列算法方面，SHA-1 曾被广泛使用，但由于人们已经发现了一些针对该算法理论上可行的攻击方式，因此该算法不应再被用于新的用途。今后我们应该主要使用的算法包括目前已经在广泛使用的 SHA-2，以及具有全新结构的 SHA-3 算法。散列函数可以单独使用，也可以作为消息认证、数字签名以及伪随机数生成器等技术的组成元素来使用。

主要应用

主要算法

MD5

MD5消息摘要算法（英语：MD5 Message-Digest Algorithm），一种被广泛使用的密码散列函数，可以产生出一个 128 位（ 16 字节，被表示为 32 位十六进制数字）的散列值（hash value），用于确保信息传输完整一致。MD5 由美国密码学家罗纳德·李维斯特（Ronald Linn Rivest）设计，于 1992 年公开，用以取代 MD4 算法。这套算法的程序在 RFC 1321 中被加以规范。

2009年，中国科学院的谢涛和冯登国仅用了 2 20.96 的碰撞算法复杂度，破解了MD5的碰撞抵抗，该攻击在普通计算机上运行只需要数秒钟。2011年，RFC 6151 禁止MD5用作密钥散列消息认证码。

原理请参考： 加密技术04-哈希算法-MD5原理

SHA-1

SHA-1（英语：Secure Hash Algorithm 1，中文名：安全散列算法1）是一种密码散列函数，美国国家安全局设计，并由美国国家标准技术研究所（NIST）发布为联邦资料处理标准（FIPS）。SHA-1可以生成一个被称为消息摘要的160位（20字节）散列值，散列值通常的呈现形式为40个十六进制数。

2005年，密码分析人员发现了对SHA-1的有效攻击方法，这表明该算法可能不够安全，不能继续使用，自2010年以来，许多组织建议用SHA-2或SHA-3来替换SHA-1。Microsoft、Google以及Mozilla都宣布，它们旗下的浏览器将在2017年停止接受使用SHA-1算法签名的SSL证书。

2017年2月23日，CWI Amsterdam与Google宣布了一个成功的SHA-1碰撞攻击，发布了两份内容不同但SHA-1散列值相同的PDF文件作为概念证明。

2020年，针对SHA-1的选择前缀冲突攻击已经实际可行。建议尽可能用SHA-2或SHA-3取代SHA-1。

原理请参考： 加密技术05-哈希算法-SHA系列原理

SHA-2

SHA-2，名称来自于安全散列算法2（英语：Secure Hash Algorithm 2）的缩写，一种密码散列函数算法标准，由美国国家安全局研发，由美国国家标准与技术研究院（NIST）在2001年发布。属于SHA算法之一，是SHA-1的后继者。其下又可再分为六个不同的算法标准，包括了：SHA-224、SHA-256、SHA-384、SHA-512、SHA-512/224、SHA-512/256。

SHA-2 系列的算法主要思路和 SHA-1 基本一致

原理请参考： 加密技术05-哈希算法-SHA系列原理

SHA-3

SHA-3 第三代安全散列算法(Secure Hash Algorithm 3)，之前名为 Keccak 算法。

Keccak 是一个加密散列算法，由 Guido Bertoni，Joan Daemen，Michaël Peeters，以及 Gilles Van Assche 在 RadioGatún 上设计。

2012年10月2日，Keccak 被选为 NIST 散列函数竞赛的胜利者。SHA-2 目前没有出现明显的弱点。由于对 MD5、SHA-0 和 SHA-1 出现成功的破解，NIST 感觉需要一个与之前算法不同的，可替换的加密散列算法，也就是现在的 SHA-3。

SHA-3 在2015年8月5日由 NIST 通过 FIPS 202 正式发表。

原理请参考： 加密技术05-哈希算法-SHA系列原理

算法对比