语音增强之谱减法
Posted qq_37215867
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了语音增强之谱减法相关的知识,希望对你有一定的参考价值。
语音增强之谱减法
原理介绍
谱减法 (Spectral Subtraction) 是最早出现的语音增强算法之一,由于实现简单且实时性较好,获得了广泛的应用。它假设语音和噪声是加性混合,且噪声是缓慢变化的,通过在静音段估计和更新噪声频谱,从带噪语音谱中减去噪声来增强语音。
设
y
(
n
)
y(n)
y(n) 为带噪语音信号,由纯净语音信号
x
(
n
)
x(n)
x(n) 和 噪声信号
d
(
n
)
d(n)
d(n) 混合形成
y
(
n
)
=
x
(
n
)
+
d
(
n
)
y(n)=x(n)+d(n)
y(n)=x(n)+d(n)
对等式两边做傅里叶变换转换到频域
Y
(
ω
)
=
X
(
ω
)
+
D
(
ω
)
Y(\\omega)=X(\\omega)+D(\\omega)
Y(ω)=X(ω)+D(ω)
Y
(
ω
)
Y(\\omega)
Y(ω)也可以表示成极坐标形式
Y
(
ω
)
=
∣
Y
(
ω
)
∣
e
j
ϕ
y
(
ω
)
Y(\\omega)=|Y(\\omega)|e^j\\phi_y(\\omega)
Y(ω)=∣Y(ω)∣ejϕy(ω)
其中
∣
Y
(
ω
)
∣
|Y(\\omega)|
∣Y(ω)∣为幅度谱,
ϕ
y
(
ω
)
\\phi_y(\\omega)
ϕy(ω)为相位谱,
D
(
ω
)
D(\\omega)
D(ω)也可以表示成
D
(
ω
)
=
∣
D
(
ω
)
∣
e
j
ϕ
d
(
ω
)
D(\\omega)=|D(\\omega)|e^j\\phi_d(\\omega)
D(ω)=∣D(ω)∣ejϕd(ω),谱减法是在幅度谱上进行的,
∣
D
(
ω
)
∣
|D(\\omega)|
∣D(ω)∣无法获得,但是可以用静音段(无语音活动的片段)的平均频谱进行估计和更新,由于相位对于语音的可懂度和质量影响较小,所以用带噪相位
ϕ
y
(
ω
)
\\phi_y(\\omega)
ϕy(ω)来代替,纯净语音谱的估计为
X
^
(
ω
)
=
(
∣
Y
(
ω
)
∣
−
∣
D
^
(
ω
)
∣
)
e
j
ϕ
y
(
ω
)
\\hatX(\\omega)=(|Y(\\omega)|-|\\hatD(\\omega)|)e^j\\phi_y(\\omega)
X^(ω)=(∣Y(ω)∣−∣D^(ω)∣)ejϕy(ω)
对估计结果做傅里叶逆变换即可得到增强后的语音。上述的
∣
Y
(
ω
)
∣
−
∣
D
^
(
ω
)
∣
|Y(\\omega)|-|\\hatD(\\omega)|
∣Y(ω)∣−∣D^(ω)∣过程可能会产生负的幅度值,这显然是有问题的,早期的做法是通过半波整流将负值直接置零
∣
X
^
(
ω
)
∣
=
∣
Y
(
ω
)
∣
−
∣
D
^
(
ω
)
∣
if
∣
Y
(
ω
)
∣
>
∣
D
^
(
ω
)
∣
0
else
|\\hatX(\\omega)|=\\begincases |Y(\\omega)|-|\\hatD(\\omega)| & \\text if |Y(\\omega)|>|\\hatD(\\omega)| \\\\ 0 & \\text else \\endcases
∣X^(ω)∣=∣Y(ω)∣−∣D^(ω)∣0 if ∣Y(ω)∣>∣D^(ω)∣ else
谱减法可以拓展到功率谱,假定
d
(
n
)
d(n)
d(n)为零均值,且
d
(
n
)
d(n)
d(n)和
x
(
n
)
x(n)
x(n)不相关,由幅度谱减公式两边平方,去掉交叉项后得到
∣
X
^
(
ω
)
∣
2
=
∣
Y
(
ω
)
∣
2
−
∣
D
^
(
ω
)
∣
2
|\\hatX(\\omega)|^2=|Y(\\omega)|^2-|\\hatD(\\omega)|^2
∣X^(ω)∣2=∣Y(ω)∣2−∣D^(ω)∣2
∣
X
^
(
ω
)
∣
2
|\\hatX(\\omega)|^2
∣X^(ω)∣2也可能出现负值,可用前述的半波整流方法处理,上式也可以写成:
∣
X
^
(
ω
)
∣
2
=
H
2
(
ω
)
∣
Y
(
ω
)
∣
2
|\\hatX(\\omega)|^2=H^2(\\omega)|Y(\\omega)|^2
∣X^(ω)∣2=H2(ω)∣Y(ω)∣2
其中
H
(
ω
)
=
1
−
∣
D
^
(
ω
)
∣
2
∣
Y
(
ω
)
∣
2
H(\\omega)=\\sqrt1-\\frac|\\hatD(\\omega)|^2|Y(\\omega)|^2
H(ω)=1−∣Y(ω)∣2∣D^(ω)∣2
H
(
ω
)
H(\\omega)
H(ω)为增益函数或抑制函数,取值范围为
0
≤
H
(
ω
)
≤
1
0\\le H(\\omega) \\le 1
0≤H(ω)≤1。
综上,谱减法更通用的形式可定义为
∣
X
^
(
ω
)
∣
p
=
∣
Y
(
ω
)
∣
p
−
∣
D
^
(
ω
)
∣
p
|\\hatX(\\omega)|^p=|Y(\\omega)|^p-|\\hatD(\\omega)|^p
∣X^(ω)∣p=∣Y(ω)∣p−∣D^(ω)∣p
缺点和改进
谱减法最显著的缺点是会引入“音乐噪声”,由于谱减过程中可能出现负的幅度值,半波整流是一种直接的解决办法,但是这种非线性处理会导致频谱随机频率位置上出现小的、独立的峰值,在时域中表现为明显的多频颤音,也称为“音乐噪声”。如果处理不当,在某些语音段,“音乐噪声”的影响甚至比干扰噪声更为明显。造成“音乐噪声”的常见原因有:
- 对谱减过程中负值的非线性处理。
- 噪声谱估计不匹配。静音段的平均噪声谱可能与实际语音段的噪声分量有着较大差别,相减后会有残留的孤立噪声段。
- 谱估计方法的误差。例如周期图等有偏功率谱估计方法带来的偏差。
- 抑制函数有较大的可变性。
为了减小音乐噪声,学者们提出了一系列的改进方法,感兴趣的读者可以自行了解。这里介绍Boll使用的方法,相比直接置零,该方法设置了一个谱值下限。在噪声估计阶段,计算一个最大噪声帧,如果谱减后某时频点的值小于最大噪声帧的对应频点值,则将其替换为相邻帧的最小值。具体可表示为:
∣
X
i
^
(
ω
)
∣
=
∣
Y
i
(
ω
)
∣
−
∣
D
^
(
ω
)
∣
if
∣
Y
i
(
ω
)
∣
−
∣
D
^
(
ω
)
∣
>
m
a
x
∣
D
^
(
ω
)
∣
min
j
=
i
−
1
,
i
,
i
+
1
∣
X
i
^
(
ω
)
∣
else
|\\hatX_i(\\omega)|=\\begincases |Y_i(\\omega)|-|\\hatD(\\omega)| & \\text if |Y_i(\\omega)|-|\\hatD(\\omega)| > max|\\hatD(\\omega)| \\\\ \\undersetj=i-1,i,i+1\\min |\\hatX_i(\\omega)| & \\text else \\endcases
∣Xi^(ω)∣=∣Yi(ω)∣信号去噪基于谱减法去噪matlab源码
一、简介
在语音去噪中最常用的方法是谱减法,谱减法是一种发展较早且应用较为成熟的语音去噪算法,该算法利用加性噪声与语音不相关的特点,在假设噪声是统计平稳的前提下,用无语音间隙测算到的噪声频谱估计值取代有语音期间噪声的频谱,与含噪语音频谱相减,从而获得语音频谱的估计值。谱减法具有算法简单、运算量小的特点,便于实现快速处理,往往能够获得较高的输出信噪比,所以被广泛采用。该算法经典形式的不足之处是处理后会产生具有一定节奏性起伏、听上去类似音乐的“音乐噪声”。
转换到频域后,这些峰值听起来就像帧与帧之间频率随机变化的多频音,这种情况在清音段尤其明显,这种由于半波整流引起的“噪声”被称为“音乐噪声”。从根本上,通常导致音乐噪声的原因主要有:
(1)对谱减算法中的负数部分进行了非线性处理
(2)对噪声谱的估计不准
(3)抑制函数(增益函数)具有较大的可变性
1 原理


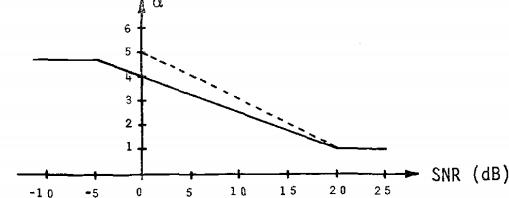

二、源代码
三、运行结果
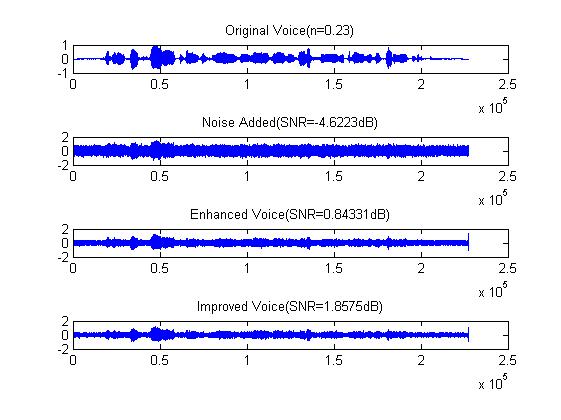
四、备注
完整代码或者仿真咨询添加QQ1575304183
以上是关于语音增强之谱减法的主要内容,如果未能解决你的问题,请参考以下文章