基于 attention 机制的 LSTM 神经网络 超短期负荷预测方法学习记录

Posted 2022-09-14 彭祥.

LSTM（long short-term memory)长短期记忆

基础介绍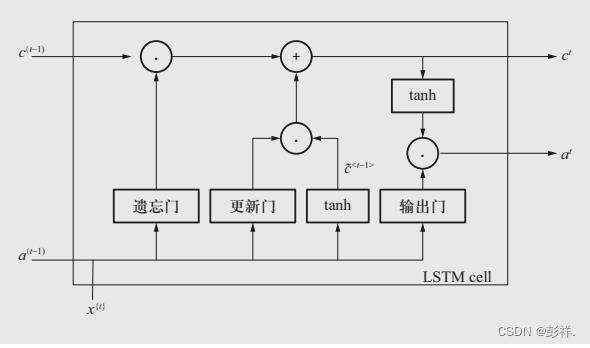

在标准LSTM体系结构中，有1个记忆单元状态和3个门，即更新门Γu、遗忘门Γf和输出门Γo，标准LSTM的体系结构如图2所示。采用x 1, x 2, …, x T
表示LSTM网络中的典型输入序列，则其中x t表示时间t时的输入特征。为了实现重要信息长时间存储，在LSTM的整个周期内设立并维护一个记忆单元c。根据前一时间的激活单元a <t–1>和当前时间的输入x ，通过3个门确定更新、维护或遗忘内部状态向量的具体元素。

标准LSTM网络采用编码器—解码器（encodedecode）结构，将输入序列编码成固定长度的向量表示。当输入序列长度较短时，有较好的学习效果，但当输入序列长度较长时，容易造成信息丢失，难以学到输入序列合理的向量表示。

优势

相较于传统的RNN,其克服了存在的梯度消失和梯度爆炸问题。

不足

LSTM网络的预测效果远优于RNN。然而LSTM网络是将所有输入特征编码成固定长度的向量表示，忽视了其与待预测负荷之间的关联性大小，因而无法有侧重地对历史数据加以利用。

实验过程

模型概述

attention机制模拟人脑注意力模型，其主要思想是针对输入序列中影响输出结果的关键部分分配较多的注意力，以更好地学习输入序列中的信息。本文将attention机制作为2个LSTM网络的接口，首先通过一个LSTM网络处理输入序列，实现高层次的特征学习；随后通过合理分配注意力权重，实现记忆单元求解；最后通过再运行一个LSTM网络实现超短期负荷预测。

模型展示

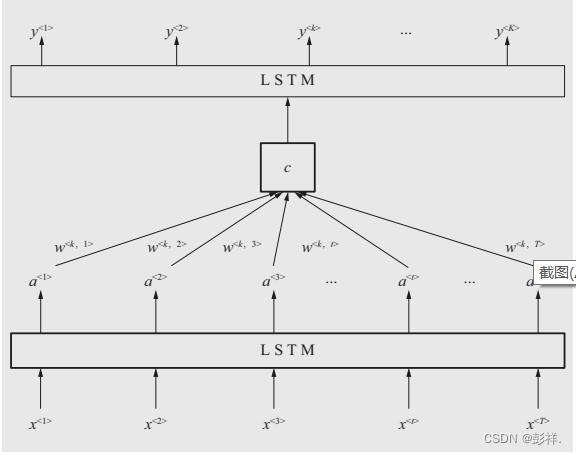
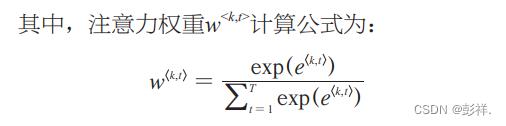
模型训练方法

损失函数

均方误差（mean squared error，MSE）用于反映估计量与被估计量之间的差异程度，将其作为本网络的目标损失函数，其计算公式为：

优化器

选用Adam算法替代传统随机梯度下降过程，基于训练数据和损失函数计算各参数的一阶矩估计及二阶矩估计，并针对计算结果动态调整每个参数的学习速率，实现网络权重的迭代更新。训练过程采用学习速度（learning rate，Ir）呈指数规律下降的方式，实现训练后期最优解的确定。经多次训练后，选取最佳优化结果。

关于Adam

Adam 是一种可以替代传统随机梯度下降（SGD）过程的一阶优化算法，它能基于训练数据迭代地更新神经网络权重。
Adam介绍

网络评价指标

平均绝对百分误差（mean absolute percentage error，MAPE）是一种常用于衡量预测准确性的指标。本文通过该指标对网络的负荷预测结果做出评判，其计算公式为：

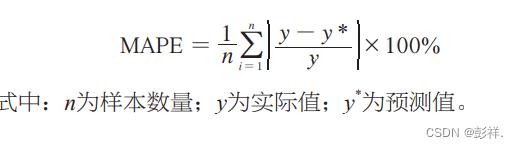
之后，该模型与标准BP网络相对比，在性能上有了明显提升。