锂离子电池健康状态估计基于粒子滤波算法的锂电池剩余使用寿命预测，python+Matlab

Posted 2023-04-04 絮沫

相关源码和数据文件已经更新在github：https://github.com/Wuito/Estimation-of-residual-life-of-particle-filter-lithium-ion-battery

粒子滤波采样

粒子滤波算法的完整建立在Gordon，Salmond和Smith提出的重采样技术上，并且一种新的采样算法（采样-重要性重采样）的发现和不断改良也对粒子滤波算法进行了丰富。

粒子滤波重采样

常用的重采样方法可以分为四类：最临近值重采样法，双线性重采样法，双立方重采样法，插值重采样法。
1）最邻近值重采样法:指的是比较目标图像与原图像的宽或者高，并且以此将原图像相对位置的像素点作为目标图像像素点的值。
2）双线性重采样法:指的是参考原图像对应像素周围四个点的值，并且由相对位置为每个点取权值来获得目标图像。
3）双立方重采样法:参考原像素点周围4*4个像素的值，并且根据这来获得目标图像。
4）插值重采样法:相比上述算法，这种方法参考更多原图像数据信息，可被用于求解对称矩阵方程组的求解以及特征值问题，重采样效果一般更好。
重采样算法是按概率进行复制和淘汰步骤，权重高的可能会被多次复制，这就保证了整体粒子数基本不变，然后进行归一化，将所有的粒子的权重都变为 1/n，继续进行下一步的预测更新步骤。虽然重采样的应用不会彻底根除粒子退化问题，但也会大大改善了粒子退化问题。
虽然重采样方法能够一定程度上减弱粒子退化问题，但是也必然会导致例子多样性的丧失，即N=1/(∑▒W_K^i )，N越小粒子退化问题也就越严重，就更加需要重采样，这样多次的重采样当然也会减慢粒子滤波的速度。

电池容量衰减模型

根据电池容量计算公式：Q=∫_tc^td▒〖I(t)dt〗,其中tc表示的是充电时间，td表示的是电池放电时间，I(t)表示的是电流，Q为锂离子电池的实时容量，而经过时间t则是记录了电池从循环开始到实验结束的时间。经过Matlab曲线拟合工具箱对四种电池容量数据进行指数拟合，能够得到比较准确的指数衰退模型。

根据电池衰减模型，我们选用双指数经验模型。

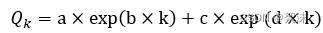
Q表示的是k时刻的电池容量，其中，k为循环次数，a,b,c,d均与锂离子电池本身有关，所以当a,b,c,d估算越准确，那么对于电池本身的模拟也就越真实，也就越能准确预测电池寿命。

算法流程

总结粒子滤波算法方法，有流程图：

使用Python3.8、Numpy1.23、matplotlib3.6软件环境对上述算法进行设计。运行Python程序可以得到CS2电池的容量预测图，在实验中以CS2_36为样本集，对样本的前600个数据进行10:1随机抽样后使用Matlab拟合工具箱对双指数模型进行拟合。

曲线拟合

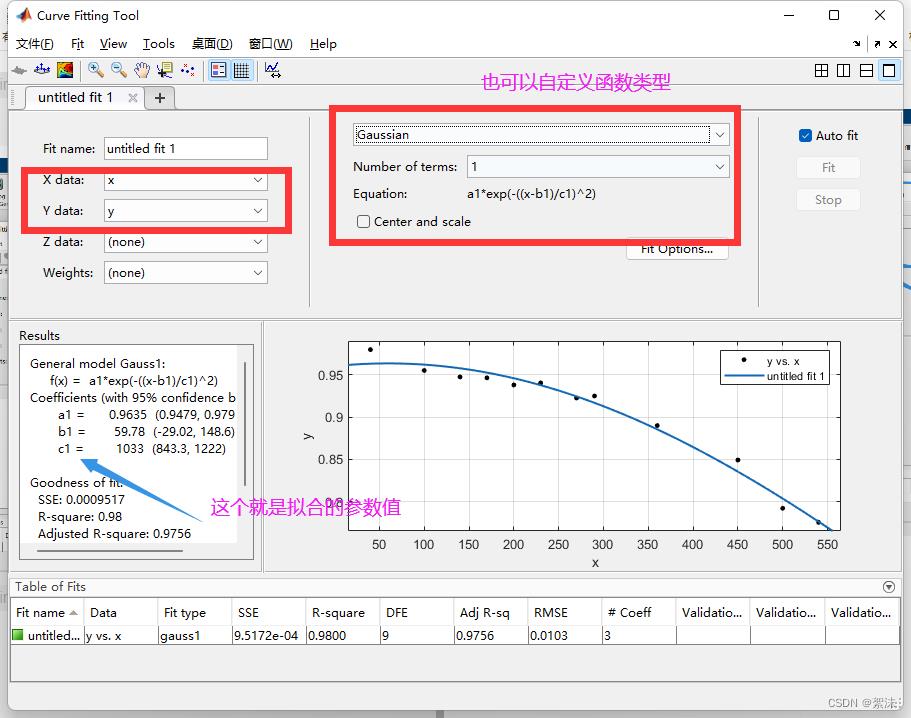
有了拟合的参数和算法方程，那就开始滤波了：
注意这里python加载的数据先前就已经计算好保存下来的数据

这是我工程的文件结构。你需要在上一篇博客里下载好马里兰大学的数据，处理好数据后保存为npy格式的文件，然后在这里应用。

先上粒子滤波的效果图：

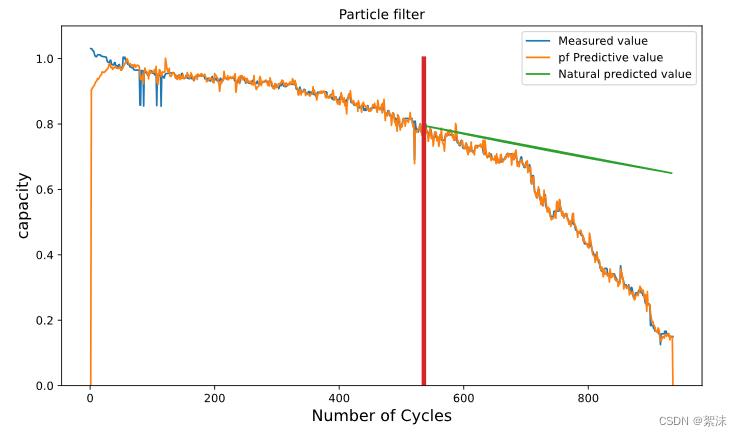
蓝色是观测值，黄色是滤波计算值，从红色线开始，绿色是没有滤波的自然观测计算值。

# 基于粒子滤波的锂离子电池RUL预测
# From: SWUST IPC14 Dai
import numpy as np
import matplotlib.pyplot as plt
from scipy.linalg import sqrtm
# Python3.8、Numpy1.23、matplotlib3.6
# 除去数据异常的较大值和较小值点
def drop_outlier(array, count, bins):
    index = []
    range_ = np.arange(1, count, bins)
    for i in range_[:-1]:
        array_lim = array[i:i + bins]
        sigma = np.std(array_lim)
        mean = np.mean(array_lim)
        th_max, th_min = mean + sigma * 2, mean - sigma * 2
        idx = np.where((array_lim < th_max) & (array_lim > th_min))
        idx = idx[0] + i
        index.extend(list(idx))
    return np.array(index)

# 剩余容量双指数方程，状态方程
def hfun(X, k):
    Q = X[0] * np.exp(X[1] * k) + X[2] * np.exp(X[3] * k)
    return Q

# 重采样步骤：
# 预测：抽取新粒子
# 更新：更新粒子权值
# 状态估计
# 多项式重采样

# 重采样
def randomR(inIndex, q):
    outIndex = np.zeros(np.shape(inIndex))
    num = np.shape(q)
    u = np.random.rand(num[0], 1)
    u = np.sort(u, axis = 0)
    u = np.array(u)
    l = np.cumsum(q, axis=0)
    i = 0
    for j in np.arange(0, num[0]):
        while (i <= (num[0]-1)) and (u[i] <= l[j]):
            outIndex[i] = j
            i = i + 1
    return outIndex

# capacity：阶段放电容量
# resistance：放电阶段电池的的内阻平均值
# CCCT：恒定电流充电时间
# CVCT: 恒定电压充电时间
if __name__ == "__main__":

    # ========================================
    #                加载数据
    # ========================================
    Battery_name = 'CS2_38'
    Battery = np.load('dataset/' + Battery_name + '.npy', allow_pickle=True)
    Battery = Battery.item()
    battery = Battery[Battery_name]

    names = ['capacity', 'resistance', 'CCCT', 'CVCT']
    # battery[1] = battery[1] /(battery[1] + 1.1)

	# 粒子滤波步骤
    # 初始化
    # 更新粒子状态
    # 权值计算和归一化
    # 重采样
    # 判断程序是否结束，迭代

    # ========================================
    #           预估数据为电池容量
    # ========================================
    N = len(battery['cycle'])
    pf_Number = 200                # 粒子数
    Prediction_Interval = 300      # 未来趋势值,预测区间的大小
    cita = 1e-4
    wa = 0.000001                  # 设定状态初始值
    wb = 0.01
    wc = 0.1
    wd = 0.0001
    Q = cita * np.diag([wa, wb, wc, wd])  # Q为过程噪声方差矩阵，diag()创建指定对角矩阵

    F = np.eye(4)   # F为驱动计算矩阵，eye()单位对角矩阵
    R = 0.001       # 观测噪声的协方差
    # ========= 状态方程赋初值 ==============
    a = -0.0000083499
    b = 0.055237
    c = 0.90097
    d = -0.00088543
    X0 = np.mat([a, b, c, d]).T  # 矩阵转置

    # ========= 滤波器状态初始化 ==============
    Xpf = np.zeros([4, N])
    Xpf[:, 0:1] = X0  # 对齐数组

    # ========= 粒子集初始化 ==============
    Xm = np.zeros([4, pf_Number, N])
    for i in np.arange(0, pf_Number - 1):
        sqr1 = np.array(sqrtm(Q))
        sqr2 = sqr1.dot(np.random.randn(4, 1))  # 矩阵乘法，直接用*是矩阵点乘
        Xm[:, i:i + 1, 0] = X0 + sqr2  # 对齐数组,需要将矩阵对齐后才能相加

    # ========= 从数据集读取观测量 =============
    capacity = battery[names[0]]
    Z = np.array(capacity)
    # ========= Zm为滤波器预测观测值，Zm与Xm对应 =============
    Zm = np.zeros([1, pf_Number, N])
    # ========= Zpf与Xpf对应 =============
    Zpf = np.zeros([1, N])         # 计算中得到的Zpf为滤波器更新得到的容量值
    # ========= 权值初始化 =============
    Weight = np.zeros([N, pf_Number])    # 计算中得到的W为更新的粒子权重

    # 粒子滤波算法
    for k in np.arange(1, N - 1):
        # 重要性采样
        for i in np.arange(0, pf_Number - 1):
            sqr1 = np.array(sqrtm(Q))       # 观测噪声
            sqr2 = sqr1.dot(np.random.randn(4, 1))  # 矩阵乘法，直接用*是矩阵点乘
            Xm[:, i:i + 1, k] = F.dot(Xm[:, i:i + 1, k - 1]) + sqr2
        # 权值重要性计算
        for i in np.arange(0, pf_Number - 1):
            Zm[0, i:i + 1, k] = hfun(Xm[:, i:i + 1, k], k)      # 观测预测
            Weight[k, i] = np.exp(-(Z[k] - Zm[0, i:i + 1, k:k + 1]) ** 2 / 2 / R) + 1e-99  # 重要性权值计算，乘方用 **
        Weight[k, :] = Weight[k, :] / sum(Weight[k, :])    # 权值归一化
        # 重采样
        # 这里的重采样以权值为传入值，返回值为采样后的索引
        outlndex = randomR(np.arange(0, pf_Number), Weight[k, :])
        # 得到新的样本
        for i in np.arange(0, len(outlndex)):
            Xm[:, i, k] = Xm[:, int(outlndex[i]), k]
        # 滤波后的状态更新，更新参数[a,b,c,d]
        Xpf[:, k] = [np.mean(Xm[0, :, k]),
                     np.mean(Xm[1, :, k]),
                     np.mean(Xm[2, :, k]),
                     np.mean(Xm[3, :, k])]
        # 更新后的状态计算预测的容量值
        Zpf[0, k] = hfun(Xpf[:, k], k)

    # ========================================
    #         计算自然条件下的预测值
    # ========================================
    start = N - Prediction_Interval    # 预测的区间
    Zf = np.zeros(Prediction_Interval)  # 自然预测值
    Xf = np.zeros(Prediction_Interval)
    for k in np.arange(start-1, N-1):
        Zf[k-start] = hfun(Xpf[:, start], k)
        Xf[k-start] = k

    # 画线
    nax = [start, start]
    nay = [0, 1]
    plt.figure(figsize=(12, 9))
    plt.title('Particle filter  '+ Battery_name)  # 折线图标题
    plt.xlabel('Number of Cycles', fontsize=14)
    plt.ylim((0, 1.1))
    plt.ylabel(names[0], fontsize=14)
    plt.plot(battery['cycle'],  Z,          markersize=3)
    plt.plot(battery['cycle'],  Zpf[0, :],  markersize=3)
    plt.plot(Xf,                Zf,         markersize=3)
    plt.plot(nax,               nay,        linewidth=4)
    plt.legend(['Measured value', 'pf Predictive value', 'Natural predicted value'])
    plt.show()

Matlab的粒子滤波

main.m

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% 版权声明：
%     本程序的详细中文注释请参考
%     黄小平，王岩，缪鹏程.粒子滤波原理及应用[M].电子工业出版社，2017.4
%     书中有原理介绍+例子+程序+中文注释
%     如果此程序有错误，请对提示修改
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%  函数功能：粒子滤波用于电源寿命预测
% function main
 

load Battery_Capacity
%%load Battery_Capacity
N=length(A5Cycle);
% error('下面的参数M请参考书中的值设置，然后删除本行代码')
M=200;   %%粒子数
Future_Cycle=100;  % 未来趋势
if N>260
    N=260;   % 过滤大于260的数字
end
 %过程噪声协方差Q
cita=1e-4;
wa=0.000001;wb=0.01;wc=0.1;wd=0.0001;
Q=cita*diag([wa,wb,wc,wd]);
 %驱动矩阵
F=eye(4);
 %观测噪声协方差
R=0.001;
 
a=-0.0000083499;b=0.055237;c=0.90097;d=-0.00088543;
X0=[a,b,c,d]';
 %滤波器状态初始化
Xpf=zeros(4,N);
Xpf(:,1)=X0;
 
% 粒子集初始化
Xm=zeros(4,M,N);
for i=1:M
    Xm(:,i,1)=X0+sqrtm(Q)*randn(4,1);
end
 
% 观测量
Z(1,1:N)=A12Capacity(1:N,:)';
 
Zm=zeros(1,M,N);
 
Zpf=zeros(1,N);
 
W=zeros(N,M);
 %粒子滤波算法
for k=2:N
    %  采样
    for i=1:M
        Xm(:,i,k)=F*Xm(:,i,k-1)+sqrtm(Q)*randn(4,1);
    end
        
    % 权值重要性计算
    for i=1:M
   
        Zm(1,i,k)=feval('hfun',Xm(:,i,k),k);
       
        W(k,i)=exp(-(Z(1,k)-Zm(1,i,k))^2/2/R)+1e-99;
    end,
 
    W(k,:)=W(k,:)./sum(W(k,:));
  
    % 重采样
    outIndex = randomR(1:M,W(k,:)');      % 调用外部函数
     % 得到新样本
    Xm( :,  :,  k)=Xm(  :,  outIndex,  k);
    % 滤波后的状态更新
    Xpf(:,k)=[mean(Xm(1,:,k));mean(Xm(2,:,k));mean(Xm(3,:,k));mean(Xm(4,:,k))];
    % 更新后的状态计算
    Zpf(1,k)=feval('hfun',Xpf(:,k),k);
end
 %预测未来电容的趋势
start=N-Future_Cycle;
for k=start:N
    Zf(1,k-start+1)=feval('hfun',Xpf(:,start),k);
    Xf(1,k-start+1)=k;
end

Xreal=[a*ones(1,M);b*ones(1,M);c*ones(1,M);d*ones(1,M)];
figure
subplot(2,2,1);
hold on;box on;
plot(Xpf(1,:),'-r.');plot(Xreal(1,:),'-b.')
legend('粒子滤波后的a','平均值a')
subplot(2,2,2);
hold on;box on;
plot(Xpf(2,:),'-r.');plot(Xreal(2,:),'-b.')
legend('粒子滤波后的b','平均值b')
subplot(2,2,3);
hold on;box on;
plot(Xpf(3,:),'-r.');plot(Xreal(3,:),'-b.')
legend('粒子滤波后的c','平均值c')
subplot(2,2,4);
hold on;box on;
plot(Xpf(4,:),'-r.');plot(Xreal(4,:),'-b.')
legend('粒子滤波后的d','平均值d')

figure
hold on;box on;
plot(Z,'-b.') 
plot(Zpf,'-r.')
plot(Xf,Zf,'-g.') 
bar(start,1,'y')
legend('实验测量数据','滤波估计数据','自然预测数据')
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

hfun.m

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% 版权声明：
%     本程序的详细中文注释请参考
%     黄小平，王岩，缪鹏程.粒子滤波原理及应用[M].电子工业出版社，2017.4
%     书中有原理介绍+例子+程序+中文注释
%     如果此程序有错误，请对提示修改
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% 函数名称：电容的观测函数
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
function Q=hfun(X,k)
Q=X(1)*exp(X(2)*k)+X(3)*exp(X(4)*k);
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

randomR.m

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% 版权声明：
%     本程序的详细中文注释请参考
%     黄小平，王岩，缪鹏程.粒子滤波原理及应用[M].电子工业出版社，2017.4
%     书中有原理介绍+例子+程序+中文注释
%     如果此程序有错误，请对提示修改 
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
function outIndex = randomR(inIndex,q);
if nargin < 2
    error('Not enough input arguments.'); 
end
outIndex=zeros(size(inIndex));
[num,col]=size(q);
u=rand(num,1);
u=sort(u);
l=cumsum(q);
i=1;
for j=1:num
    while (i<=num)&(u(i)<=l(j))
        outIndex(i)=j;
        i=i+1;
    end
end

滤波估计基于matlab双卡尔曼滤波SOC和SOH联合估计含Matlab源码 2335期

⛄一、双卡尔曼滤波SOC和SOH联合估计

1 引言
为实现节能降耗，降低污染，发展节能环保、不依赖化石燃料的电动汽车取代传统燃油车，已成为当今世界汽车行业的重点发展方向。锂离子动力电池准确可靠的状态估计是电动汽车安全运行的基础[1]，其主要包括荷电状态（SOC）和健康状态（SOH）。SOC直接反映了电池剩余电量的大小，其准确估计直接关系到电动汽车的能量动力分配。

SOH是电池老化程度的一项重要指标，通常表现为电池的能量密度、功率密度、容量的衰减和内部电阻增大[2]，电池状态的准确估计可以使电池得到充分合理的利用，避免电池突发故障造成的危害，对于电动汽车的安全运行具有重要意义[3]。

目前国内应用最多的电池SOC测量方法是安时积分法，它计算简单，但受初始SOC误差的影响较大，且会随时间增长出现较大的累计误差[4]。另外，电池SOC测量方法还有开路电压法、卡尔曼滤波法、神经网络法。开路电压法容易实现但需要通过静置校准OCV值，不利于实际运用[5]。

神经网络法通过训练大量的样本数据进行估算，准确性受训练的方法及训练量大小影响较大，计算量太大。卡尔曼滤波法使用递推迭代的方法对SOC进行估算[6]。最常用的为扩展卡尔曼滤波（EKF）和无迹卡尔曼滤波（UKF):EKF估算过程中容易由于线性化过程中方差矩阵的非正定性导致估计值不收敛；UKF利用无迹变换处理均值和协方差，可以有效提高对非线性分布统计量的估算精度，但是系统噪声的预定变量设置不当通常会导致系统误差和发散[6]。

国内外常用的SOH估计方法有定义法、电化学阻抗谱分析法、容量衰减法等。定义法是以电池的定义为基础，应用电池内部特征量变化前后的比值关系来对电池的进行估计ÿ