配电网重构SOE随机配电网重构中的开关开换方法研究（Matlab代码实现）

Posted 2023-04-03 数学建模与科研

💥 💥 💞 💞 欢迎来到本博客 ❤️ ❤️ 💥 💥


🏆 博主优势： 🌞 🌞 🌞博客内容尽量做到思维缜密，逻辑清晰，为了方便读者。


⛳ 座右铭：行百里者，半于九十。

📋 📋 📋 本文目录如下： 🎁 🎁 🎁
目录
💥1 概述
📚2 运行结果
2.1 算例结果
2.2 仿真结果
2.3 结论
🎉3 参考文献
🌈4 Matlab代码、数据、文章讲解

💥1 概述

摘要：配电网重构(DNR)的目的是确定配电网的最优拓扑结构，是降低电网功率损耗的有效措施。电力负荷需求和光伏(PV)输出是不确定的，并随时间变化，将影响最佳网络拓扑结构。单小时确定性DNR无法处理这种不确定性和可变性。为此，本文提出了求解多小时随机DNR (SDNR)的方法。现有的DNR求解方法要么不准确，要么过于耗时，因此无法求解大型配电网的多小时sdnr。为此，提出了一种开关开交换(SOE)方法。从所有开关关闭的环路网络开始，SOE由三个步骤组成。第一步是依次打开开关，直到打开所有循环。第二步和第三步修改第一步中获得的分支的状态，以获得更好的径向拓扑。通过5个试验系统验证了该方法的准确性和快速求解速度，以及多小时SDNR优于单小时确定性DNR的优越性。

📚2 运行结果

2.1 算例结果

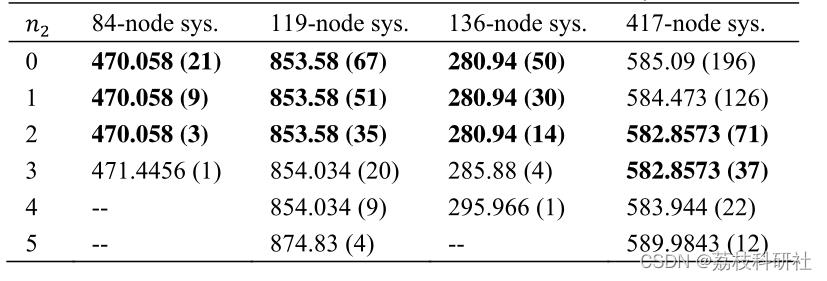
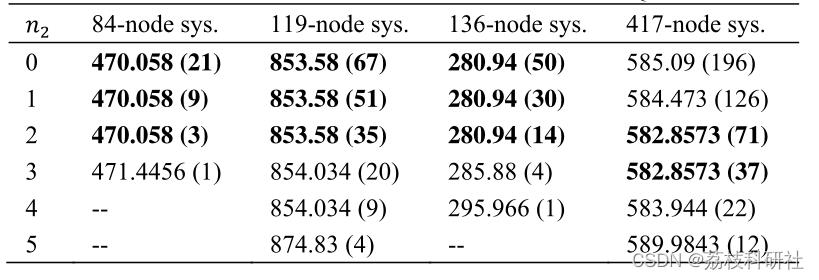
编辑

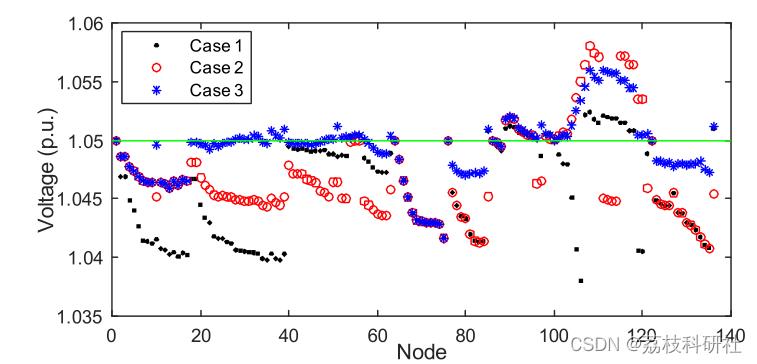
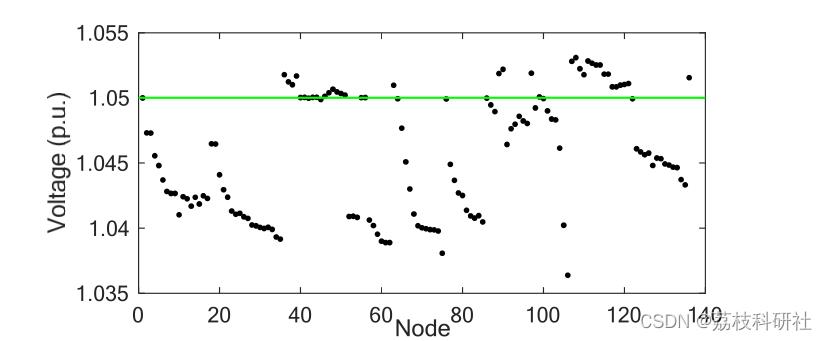
2.2 仿真结果

2.3 结论

提出了一个多小时的SDNR来处理可变和不确定的负载和PV输出。现有的SDNR方法要么不准确，要么太耗时。因此，提出了一种精确、快速的启发式方法SOE，同时求解SDNR和DDNR。SOE由三个步骤组成。第一步可以快速获得相对准确的初始解，第二步和第三步进一步提高精度。仿真结果表明，与其他启发式方法相比，SOE 1)精度更高，2)在单小时DDNRs中的精度几乎与MP相当(99.71% ~ 100%)，3)在求解多小时DDNRs时明显优于MP(例如损失减少19.65%)。SOE的解决速度明显快于MP(例如，快72-2325倍)。因此，SOE在精度和/或求解速度方面优于MP和其他启发式方法，特别是在求解大规模多小时DDNRs时。仿真结果还表明:1)解决多小时DDNR/SDNR比解决单小时DDNR/SDNR能获得更好的结果，即具有更低的损耗和/或满足电压限制;2)阻塞DDNR/SDNR能在损耗和开关动作数之间实现良好的平衡，而小时DDNR/SDNR有很多开关动作，24小时DDNR/SDNR有很高的损耗;3) SDNR优于DDNR，当负载(PV输出)低于(高于)其预测值时，DDNR的结果可能会违反电压上限。

部分代码：

warning('off')

addpath(pathdef)

mpopt = mpoption;

mpopt.out.all = 0; % do not print anything

mpopt.verbose = 0;

version_LODF = 0 % 1: use decrease_reconfig_algo_LODF.m

% 0: use decrease_reconfig_algo.m

distancePara = 10

combine3 = 1

candi_brch_bus = []; % candidate branch i added to bus j

% mpc0 = case417;

casei=4

d417_v2

substation_node = 1; n_bus = 417;

n1 = 3

n2 = 2

n1_down_substation = n1+1; n2_up_ending = n2;

Branch0 = Branch;

brch_idx_in_loop0 = unique(brch_idx_in_loop(:));

show_biograph1 = 0;

show_biograph = 0;

%% original network's power flow (not radial)

% show_biograph(Branch, Bus)

from_to = show_biograph_not_sorted(Branch, substation_node, show_biograph1);

mpc = generate_mpc(Bus, Branch, n_bus);

res_orig = runpf(mpc, mpopt);

losses = get_losses(res_orig.baseMVA, res_orig.bus, res_orig.branch);

loss0 = sum(real(losses));

fprintf('case417_tabu: original loop network''s loss is %.5f \\n\\n', loss0)

% for each branch in a loop,

% if open that branch does not cause isolation, check the two ending buses

% of that branch for connectivity, realized by shortestpath or conncomp

% calculate the lowest loss increase, print out the sorted loss increase

% open the branch with lowest loss increase

% stop criterion: number of buses - number of branches = 1

%% ------------------------ Core algorithm ------------------------%%

ff0 = Branch(:, 1); ff = ff0;

tt0 = Branch(:, 2); tt = tt0;

t1 = toc;

if version_LODF

[Branch] = decrease_reconfig_algo_LODF(Bus, Branch, brch_idx_in_loop, ...

ff0, tt0, substation_node, n_bus, loss0, distancePara); %%% core algorithm

else

[Branch] = decrease_reconfig_algo(Bus, Branch, brch_idx_in_loop, ff0, tt0, ...

substation_node, n_bus, loss0); %%% core algorithm

end

t2 = toc;

time_consumption.core = t2 - t1

% output of core algorithm

from_to = show_biograph_not_sorted(Branch(:, [1 2]), substation_node, ...

show_biograph1);

from_to0 = from_to;

mpc = generate_mpc(Bus, Branch, n_bus);

res_pf_dec = runpf(mpc, mpopt);

losses = get_losses(res_pf_dec.baseMVA, res_pf_dec.bus, res_pf_dec.branch);

loss0_dec = sum(real(losses)); %

fprintf('case417_tabu: radial network obtained by my core algorithm''s loss is %.5f \\n\\n', loss0_dec)

Branch_loss_record = [];

% record Branch and loss

Branch_loss_record.core.Branch = Branch;

Branch_loss_record.core.loss = loss0_dec;

%% prepare force open branches for tabu: branch_idx_focused

if get_brch_tabu_v2 == 1

[branch_idx_focused] = get_branch_idx_focused_for_tabu_v2( ...

from_to, Branch0, Branch, substation_node, brch_idx_in_loop0, n_bus, ...

n1_down_substation, n2_up_ending); % to answer reviewer 5-5's question

else

[branch_idx_focused] = get_branch_idx_focused_for_tabu( ...

from_to, Branch0, Branch, substation_node, brch_idx_in_loop0, n_bus, ...

n1_down_substation, n2_up_ending);

end

%% ------------------------ Tabu algorithm ------------------------%%

% run the core program for each upstream branch connected to the idx_force_open

% idx_considered = [35 69]

% for iter = idx_considered

for iter = 1:length(branch_idx_focused)

fprintf('iter=%d/%d\\n', iter, length(branch_idx_focused));

Branch = Branch0;

Branch(branch_idx_focused(iter), :) = [];

ff0 = Branch(:, 1); ff = ff0;

tt0 = Branch(:, 2); tt = tt0;

brch_idx_in_loop = brch_idx_in_loop0;

idx_tmp = find(brch_idx_in_loop == branch_idx_focused(iter));

if isempty(idx_tmp)

else

brch_idx_in_loop(idx_tmp) = [];

brch_idx_in_loop(idx_tmp:end) = brch_idx_in_loop(idx_tmp:end)-1;

end

t1 = toc;

%%------------------- core algorithm in Tabu loop--------------------%%

if version_LODF

[Branch] = decrease_reconfig_algo_LODF(Bus, Branch, brch_idx_in_loop, ...

ff0, tt0, substation_node, n_bus, loss0, distancePara); %%% core algorithm

else

[Branch] = decrease_reconfig_algo(Bus, Branch, brch_idx_in_loop, ff0, tt0, ...

substation_node, n_bus, loss0); %%% core algorithm

end

t2 = toc;

🎉3 参考文献

部分理论来源于网络，如有侵权请联系删除。

🌈4 Matlab代码、数据、文章讲解

配电网重构基于粒子群求解配电网重构模型matlab源码

一、故障信息的数学表示

在上图中K表示断路器，每一个断路器上均有一个FTU装置，可以反馈断路器开关是否过流，用表示上传的故障信息，反映的是各分段开关处是否流过故障电流有故障电流为1,否则为0）。即：

 

因为FTU上传的信息可分为有故障信息及无故障信息两类,对于分段区间来讲也只能是有故障及无故障两种情况,所以我们可以用二进制编码规则对配电网故障定位问题进行数学建模。以上图所示辐射状配电网为例,系统拥有12个分段开关,我们可以用一串12位的二进制代码表示FTU的上传信息,作为程序的输入,1代表对应的开关有过流信息,0代表对应的开关无过流信息。同时用另一串12位的二进制代码作为程序的输出,代表对应馈线区间发生故障,代表无故障。

传统配电网的运行优化问题主要涉及发电机机端电压的调整、变压器分接头的调节和电容器容量的配置。在接入分布式电源和储能装置之后，配电网的优化问题还将包括对分布式电源和储能装置的控制。配电网运行优化问题的目标函数主要有最小化系统的有功功率损耗，减少设备的运行成本等等。优化变量包括连续型变量即分布式电源和储能装置的有功无功等，离散型变量即变压器的分接头和电容器的投切组数，接入设备的位置和容量等。约束条件主要有1.发电机机端电压的最大最小限制2.变压器分接头的档位限制以及电容器的容量限制3.变压器和电容器每日最大操作数的限制， 4. 分布式电源和储能装置的有功无功功率约束等。综合配电网优化的目标函数、变量以及约束条件，该优化问题可以看作是一个多目标、多变量的混合整数非线性规划问题。
针对配电网的优化问题，目前主要的求解方法有传统的数学优化方法和人工智能方法。传统的数学优化方法主要包括线性/非线性规划法、动态规划法等，而人工智能方法主要包括遗传算法、模拟退火法和粒子群优化算法等。传统的优化算法从全局考虑整个优化问题，原理严格，计算时间较短。但是对目标函数和优化变量的初值要求较高。人工智能算法对目标函数和初值的要求不高，并且能够求解高维度的优化问题，其缺点是容易陷入局部最优，计算时间较长。
综上，配电网的优化方向主要内容有：（1）含分布式发电设备与储能设备的运行方式研究（2）配电网中接入的分布式发电设备与储能装置的安装位置和容量的选择（3）综合考虑分布式发电设备以及储能装置的运行与规划的优化问题研究

二、粒子群算法的概念

  粒子群优化算法(PSO：Particle swarm optimization) 是一种进化计算技术（evolutionary computation）。源于对鸟群捕食的行为研究。粒子群优化算法的基本思想：是通过群体中个体之间的协作和信息共享来寻找最优解．
  PSO的优势：在于简单容易实现并且没有许多参数的调节。目前已被广泛应用于函数优化、神经网络训练、模糊系统控制以及其他遗传算法的应用领域。

1、基本思想

  粒子群算法通过设计一种无质量的粒子来模拟鸟群中的鸟，粒子仅具有两个属性：速度和位置，速度代表移动的快慢，位置代表移动的方向。每个粒子在搜索空间中单独的搜寻最优解，并将其记为当前个体极值，并将个体极值与整个粒子群里的其他粒子共享，找到最优的那个个体极值作为整个粒子群的当前全局最优解，粒子群中的所有粒子根据自己找到的当前个体极值和整个粒子群共享的当前全局最优解来调整自己的速度和位置。下面的动图很形象地展示了PSO算法的过程：

2、更新规则

  PSO初始化为一群随机粒子(随机解)。然后通过迭代找到最优解。在每一次的迭代中，粒子通过跟踪两个“极值”(pbest，gbest)来更新自己。在找到这两个最优值后，粒子通过下面的公式来更新自己的速度和位置。

公式(1)的第一部分称为【记忆项】，表示上次速度大小和方向的影响；公式(1)的第二部分称为【自身认知项】，是从当前点指向粒子自身最好点的一个矢量，表示粒子的动作来源于自己经验的部分；公式(1)的第三部分称为【群体认知项】，是一个从当前点指向种群最好点的矢量，反映了粒子间的协同合作和知识共享。粒子就是通过自己的经验和同伴中最好的经验来决定下一步的运动。以上面两个公式为基础，形成了PSO的标准形式。

%function main()
clear;
clc;
tic;
psoOptions = get_psoOptions; 
psoOptions.Vars.ErrGoal = 1e-6;     %最小误差
LL=5;   %联络开关数
% Parameters common across all functions
psoOptions.SParams.c1 = 0.02; %边界参数
psoOptions.SParams.w_beta = 0.5; %初始化beta值
 
% Run experiments for the three complex functions
psoOptions.Obj.f2eval = 'fitness_4geDG';
 
psoOptions.Obj.lb = ones(1,LL); %初始化下限
%psoOptions.Obj.lb = ones(1,32);
psoOptions.Obj.ub = [10 7 15 21 11]; %初始化上限            %通过运行程序maxswarmmin得到的结果
%psoOptions.Obj.ub = 20*ones(1,32);
%psoOptions.Obj.ub(1,1:5)=4;
psoOptions.SParams.Xmax =psoOptions.Obj.ub; %最大限制位置
 
DimIters = [5; ...   %Dimensions维数
              300];    %Corresponding iterations迭代次数
  x = DimIters;        
psoOptions.Vars.Dim = x(1,:);
 psoOptions.Vars.Iterations = x(2,:);
 swarmsize = [50]   %种群规模
psoOptions.Vars.SwarmSize = swarmsize;
disp(sprintf('This experiment will optimize %s function', psoOptions.Obj.f2eval));
disp(sprintf('Population Size: %d\\t\\tDimensions: %d.', psoOptions.Vars.SwarmSize, psoOptions.Vars.Dim));
temp = 5e6;
fVal = 0;
%运行QPSO算法
 [tfxmin, xmin,PBest,fPBest, tHistory] = QPSO(psoOptions);
    fVal=tfxmin;
      if temp>tfxmin
        temp=tfxmin;
        record=tHistory;
      end
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
toc;
disp(sprintf('\\nminxfmin= \\t\\t%2.10g',temp));  %最优函数适应值
xmin           %优化的开关组合    
fPBest         %备选开关组合函数适应值
PBest          %备选开关组合(用于在哪个开关失灵情况下，采用备选方案，更加符合实际情况)
a=fbm(xmin)
figure(1)
plot(record(:,2))
xlabel('迭代次数')
ylabel('适应度值')

完整代码或者代写添加QQ1575304183