优化求解基于遗传算法求解多目标配电网重构模型matlab源码

Posted 2021-05-21 Matlab走起

一、故障信息的数学表示

在上图中K表示断路器，每一个断路器上均有一个FTU装置，可以反馈断路器开关是否过流，用表示上传的故障信息，反映的是各分段开关处是否流过故障电流有故障电流为1,否则为0）。即：

 

因为FTU上传的信息可分为有故障信息及无故障信息两类,对于分段区间来讲也只能是有故障及无故障两种情况,所以我们可以用二进制编码规则对配电网故障定位问题进行数学建模。以上图所示辐射状配电网为例,系统拥有12个分段开关,我们可以用一串12位的二进制代码表示FTU的上传信息,作为程序的输入,1代表对应的开关有过流信息,0代表对应的开关无过流信息。同时用另一串12位的二进制代码作为程序的输出,代表对应馈线区间发生故障,代表无故障。

遗传算法是从代表问题可能潜在的解集的一个种群（population）开始的，而一个种群则由经过基因（gene）编码的一定数目的个体(individual)组成。每个个体实际上是染色体(chromosome)带有特征的实体。

染色体作为遗传物质的主要载体，即多个基因的集合，其内部表现（即基因型）是某种基因组合，它决定了个体的形状的外部表现，如黑头发的特征是由染色体中控制这一特征的某种基因组合决定的。因此，在一开始需要实现从表现型到基因型的映射即编码工作。由于仿照基因编码的工作很复杂，我们往往进行简化，如二进制编码。

初代种群产生之后，按照适者生存和优胜劣汰的原理，逐代（generation）演化产生出越来越好的近似解，在每一代，根据问题域中个体的适应度（fitness）大小选择（selection）个体，并借助于自然遗传学的遗传算子（genetic operators）进行组合交叉（crossover）和变异（mutation），产生出代表新的解集的种群。

这个过程将导致种群像自然进化一样的后生代种群比前代更加适应于环境，末代种群中的最优个体经过解码（decoding），可以作为问题近似最优解。

二、 遗传算法过程图解

 

三、构造配电网故障定位评价函数

    基于待求各馈线区段实际状态下所对应的信息应与实际上传故障信息偏差最小的原则，构造如下评价函数：

 

表达式的值为每个潜在解对应的适应度值,值越小表示解越优良,因此评价函数应取极小值。

式中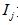：为第j个开关FTU上传的故障信息,取值为1认为该开关流过了故障电流,为0则未流过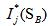；为各开关节点的期望状态,若该开关流过了故障电流,则期望状态为1,相反,期望状态为0,表达式为各区段状态的函数。N为配电网中馈线区段的总数，为配电网中各设备状态,为1表明设备故障,取0则设备正常。表示一个权系数乘以故障设备数,。是根据故障诊断理论中“最小集”概念设置的权重系数,取值范围介于与1之间,表明故障区间数越少解越优,避免出现误诊断,本文中权系数取0.5。

四、求期望函数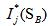

针对不同的网络，期望函数的表达式不同，无法用统一的格式表示出来。仅以上述算例为例来说明如何求取期望函数。

在辐射型配电网中,任何区间发生故障,必将导致其上游开关流过故障过电流。这是求取期望函数的原则。假设图一的馈线区段6处发生故障,那么分段开关K1,K2,K3 ,K6,都将有过电流若馈线区段11处发生故障,则K1,K2,K3 ,K6,K10都将有过电流。由此类推我们可得到各个分段开关的期望函数:

 
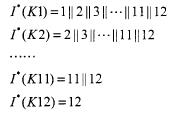
%采用改进遗传算法，基于环网的编码，便于产生可行解（满足配网辐射状的约束）
%用于IEEE33节点配电网故障恢复，适应度是计算网损和操作次数
%选择采用的是轮盘赌方式
%移位操作和变异操作后不会产生不可行解，不需要检验
 
clear;
clc;
tic
%基于环网的编码策略，公共支路只需要放在其中1个环网中，开关1不需要编码（始终闭合）
loop1=[2,3,4,5,18,19,20,33];
loop2=[22,23,24,25,26,27,28,37];
loop3=[8,9,10,11,21,35];
loop4=[6,7,15,16,17,29,30,31,32,36];
loop5=[12,13,14,34];
%确定故障支路(以txt文件形式输入)
% txtpath='breaker.txt';%文件路径名
bb=36;
%存放初始开关集
population1=[1,1,1,1,1,1,1,0,1,1,1,1,1,1,1,0,1,1,1,1,1,0,1,1,1,1,1,1,1,1,1,0,1,1,1,0]; 
%种群大小
popsize=50;
%基因块编码长度
%chromlength=5;
%移位概率
pc = 0.6;
%变异概率
pm = 0.001;
%初始种群
pop = initpop(popsize,bb);
%初始化x,y（存放每次迭代下的最优解）
x=zeros(1,50);
y=zeros(50,size(pop,2));
%计算适应度值
fitvalue = cal_fitvalue(pop);     
for i = 1:50  %50次迭代
    %选择操作
    newpop = selection(pop,fitvalue);
    %移位操作
    newpop = moveposition(newpop,pc,bb);
    %变异操作
    newpop = mutation(newpop,pm,bb);
    %更新种群
    pop = newpop;
    %计算适应度值，寻找最优解
    fitvalue = cal_fitvalue(pop);
    [bestindividual,bestfit] = best(pop,fitvalue);  
    %ws(i)=powerflow(transform(bestindividual)); %记录实际网损
    %cz(i)=sum(xor(bestindividual,population1))-1; %记录实际操作次数
    x(i)=bestfit;
    y(i,:)=bestindividual;
end
[bestfit1,index]=max(x);
%展示初始拓扑
figure
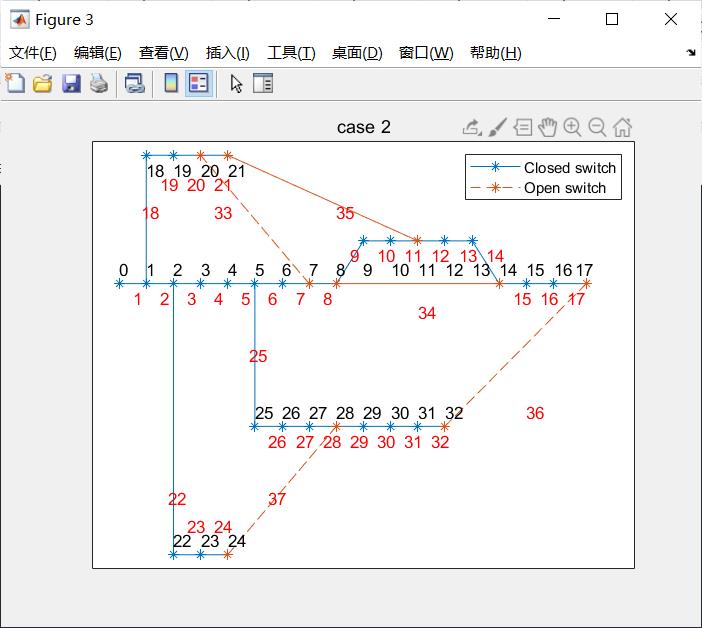
show_tuopu(population1);
saveas(gca,'tuopu1.jpg'); %将拓扑以图片格式保存输出
%展示最大适应度值对应的配网拓扑
figure
show_tuopu(y(index,:));
saveas(gca,'tuopu.jpg'); %将拓扑以图片格式保存输出
%输出各迭代次数下的最佳适应度值
x;
bestfit1;
y(index,:);
%输出具体操作开关
[openkg,closekg] = judge_kg(y(index,:),bb); %求出最优拓扑下需要关断和闭合的开关
fid=fopen('openkg.txt','wt');  %将计算结果以txt文件的形式输出
fprintf(fid,'%g\\n',openkg);
fclose(fid);
fid=fopen('closekg.txt','wt');  %将计算结果以txt文件的形式输出
fprintf(fid,'%g\\n',closekg);
fclose(fid);
%输出最佳拓扑对应下的配电网的网速和操作次数
ws = powerflow(transform(y(index,:)))
cz = sum(xor(y(index,:),population1))-1
%result=[ws;cz];
fid=fopen('ws.txt','wt');  %将计算结果以txt文件的形式输出
fprintf(fid,'%g\\n',ws);
fclose(fid);
fid=fopen('cz.txt','wt');  %将计算结果以txt文件的形式输出
fprintf(fid,'%g\\n',cz);
fclose(fid);
%输出潮流计算的节点电压
[node,u,delt]=powerflow_V(transform(y(index,:)));
nodevoltage=[node',u',delt'];
fid=fopen('nodevoltage.txt','wt');  %将计算结果以txt文件的形式输出
[m,n]=size(nodevoltage);
for i=1:m
   for j=1:n
      if j==n
          fprintf(fid,'%g\\n',nodevoltage(i,j));
      else
          fprintf(fid,'%g\\t',nodevoltage(i,j));
      end
   end
end
fclose(fid);
%输出潮流计算的支路电流
[branch,p,q]=powerflow_S(transform(y(index,:)));
branchflow=[branch',p',q']
fid=fopen('branchflow.txt','wt');  %将计算结果以txt文件的形式输出
[m,n]=size(branchflow);
for i=1:m
   for j=1:n
      if j==n
          fprintf(fid,'%g\\n',branchflow(i,j));
      else
          fprintf(fid,'%g\\t',branchflow(i,j));
      end
   end
end
fclose(fid);
toc
 

完整代码或者代写添加QQ1575304183