Python scipy.interpolate插值

Posted 2023-04-01 Windy.Zhhh

我们采集到的数据都是以离散的点的形式存在的，只有在采样点上才有具体的值，在其他区域都没有值数据。此时就需要插值分析，将采样点的数值根据一定的算法，推算出其他未采样区域的数值。

在讲scipy.interpolate类方法插值函数之前我们先讲两种常见的插值方法：待定系数法和拉格朗日法插值。

待定系数法插值：待定系数法插值在我们拥有n个插值节点时构造一个n次多项式，

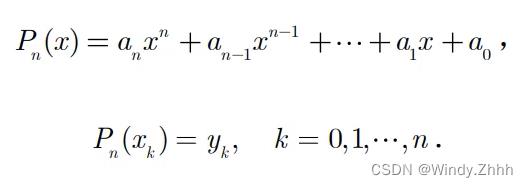
 然后可以构造非齐次线性方程组，

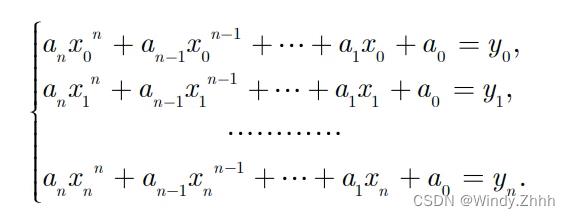
 在高数或线性代数里，我们学过范德蒙德行列式，我们可以根据上述非齐次线性方程组构造出它的系数矩阵，

再根据解线性方程组的克拉默（克莱姆） 法则，线性方程组的解确定且唯一，由此我们便可以得到我们的插值函数。

由python代码编写如下：

import numpy as np
import matplotlib.pyplot as plt
from scipy import interpolate
x0=np.linspace(-10,10,21)
y0=np.sin(x0)
plt.plot(x0,y0,'o')
A=np.vander(x0)
p=np.linalg.inv(A)@y0
x1=np.linspace(-10,10,101)
plt.plot(x1,np.polyval(p,x1))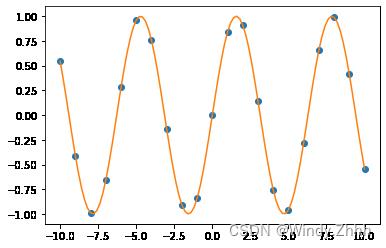

 拉格朗日插值法：相对于待定系数法更为简便，首先构造一组基函数，

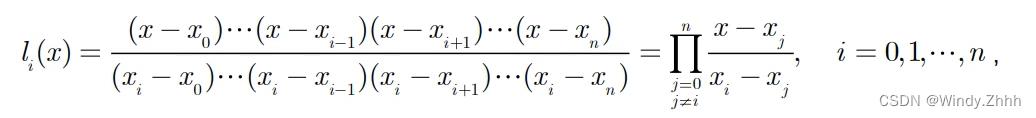
并令其满足以下条件，

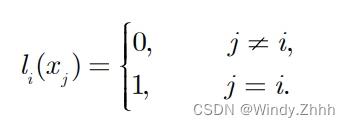
得到n次拉格朗日插值多项式，由方程组

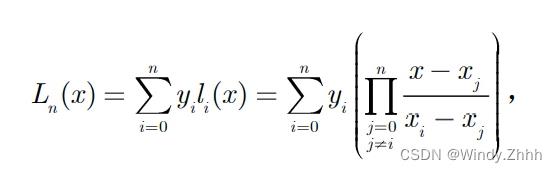
解的唯一性，n+1个节点的n次拉格朗日插值多项式存在且唯一。

python实现代码如下:

import numpy as np
from scipy import interpolate
import pylab as pl
x=np.linspace(-15,15,11)
y=np.sin(x)
pl.plot(x,y,'o')
x1=np.linspace(-15,15,101)
p=interpolate.lagrange(x,y)
pl.plot(x1,np.polyval(p,x1))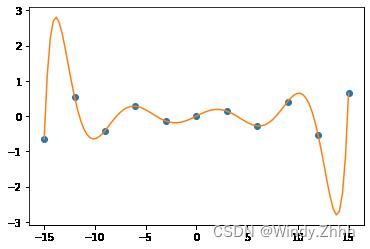

 

此外还要注意当插值次数太高产生的龙格现象。龙格现象_百度百科在计算方法中，有利用多项式对某一函数的近似逼近，计算相应的函数值。一般情况下，多项式的次数越多，需要的数据就越多，而预测也就越准确。插值次数越高，插值结果越偏离原函数的现象称为龙格现象。https://baike.baidu.com/item/%E9%BE%99%E6%A0%BC%E7%8E%B0%E8%B1%A1/5473475

import numpy as np
import matplotlib.pyplot as plt
from scipy import interpolate
x=np.linspace(-10,10,11)
y=np.sin(x)
x1=np.linspace(-10,10,101)
y1=np.sin(x1)
plt.plot(x1,y1,label='sinx')
f1=interpolate.interp1d(x,y,kind='quadratic')
f2=interpolate.interp1d(x,y,kind='cubic')
f3=interpolate.interp1d(x,y,kind=7)
f4=interpolate.interp1d(x,y,kind=9)
plt.plot(x1,f1(x1),label='2')
plt.plot(x1,f2(x1),label='3')
plt.plot(x1,f3(x1),label='5')
plt.plot(x1,f4(x1),label='9')
plt.legend()
plt.show()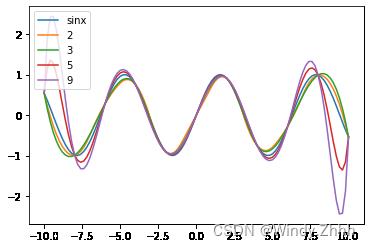

 现在我们开始讲scipy.interpolate类函数插值方法

一维插值：使用interpolate.interp1d函数插值

官方文档：

scipy.interpolate.interp1d — SciPy v1.8.1 Manual

使用时主要定义kind的类型来进行不同类别的插值

一次插值kind='inear'

二次插值kind='quadratic'

三次插值kind='cubic'

此外还有0阶插值nearest和zero方法

此两种方法使用如下：

import numpy as np
from scipy import interpolate
import matplotlib.pyplot as plt
x=np.linspace(0,10,11)
y=np.sin(x)
x1=np.linspace(0,10,101)
y1=np.sin(x1)
plt.plot(x1,y1)
f1=interpolate.interp1d(x,y,kind='nearest')
plt.plot(x1,f1(x1))
f2=interpolate.interp1d(x,y,kind='zero')
plt.plot(x1,f2(x1))
plt.plot(x,y)

可构成阶梯状曲线

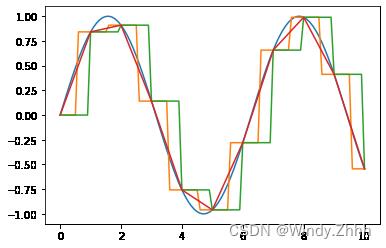
 二维插值：使用interpolate.interp2d函数插值

对模糊图像处理：

示例函数如下：

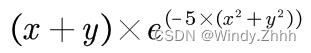
import numpy as np
import matplotlib as mpl
import pylab as pl
from scipy import interpolate

def z(x,y):
    return (x+y)*np.exp(-5*(x**2+y**2))
x,y=np.mgrid[-1:1:15j,-1:1:15j]
newfunc=interpolate.interp2d(x,y,z(x,y),kind='cubic')
xnew=np.linspace(-1,1,200)
ynew=np.linspace(-1,1,200)
fnew=newfunc(xnew,ynew)
pl.subplot(121)
im1=pl.imshow(z(x,y),origin='lower',extent=[-1,1,-1,1],cmap=mpl.cm.hot)
pl.colorbar(im1)
pl.subplot(122)
im2=pl.imshow(fnew,origin='lower',extent=[-1,1,-1,1],cmap=mpl.cm.hot)
pl.colorbar(im2)
pl.show()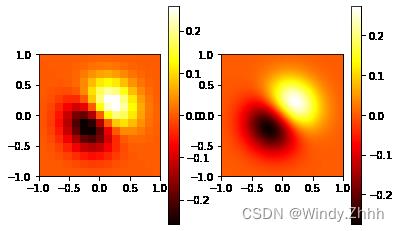

 二维插值的三维图片展示

函数仍未上示例函数

import numpy as np
import matplotlib as mpl
from scipy import interpolate
import matplotlib.pyplot as plt

def func(x, y):
    return (x + y) * np.exp(-5.0 * (x ** 2 + y ** 2))

x,y=np.mgrid[-1:1:20j,-1:1:20j]  
fvals = func(x, y)  
fig = plt.figure(figsize=(18,10))  
ax = plt.subplot(121, projection='3d')
surf = ax.plot_surface(x, y, fvals, rstride=1, cstride=1, cmap=mpl.cm.coolwarm, linewidth=0.5,
                       antialiased=True)
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.set_zlabel('z')  
plt.colorbar(surf, shrink=0.5, aspect=5,pad=0.1)  
newfunc = interpolate.interp2d(x, y, fvals, kind='cubic')  
xnew = np.linspace(-1, 1, 200) 
ynew = np.linspace(-1, 1, 200) 
fnew = newfunc(xnew, ynew)  
xnew, ynew = np.meshgrid(xnew, ynew)
ax2 = plt.subplot(122, projection='3d')
surf2 = ax2.plot_surface(xnew, ynew, fnew, rstride=1, cstride=1, cmap=mpl.cm.coolwarm, linewidth=0.5, antialiased=True)
ax2.set_xlabel('xnew')
ax2.set_ylabel('ynew')
ax2.set_zlabel('znew')
plt.colorbar(surf2, shrink=0.5, aspect=5,pad=0.1)  
plt.show()

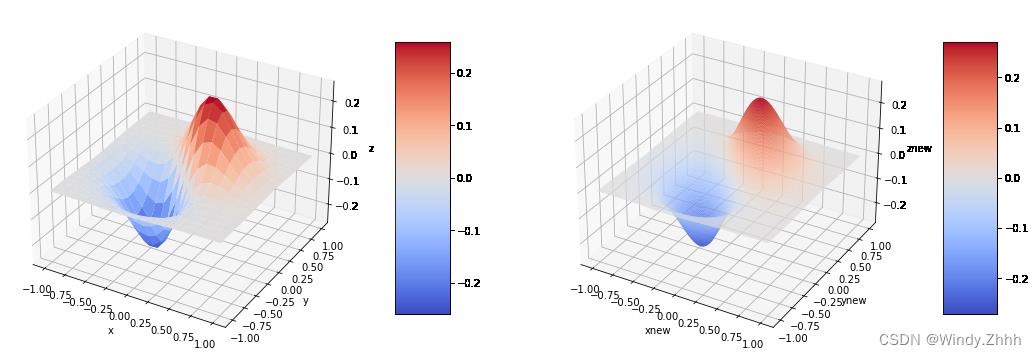
差异 scipy interpolate vs mpl griddata

【中文标题】差异 scipy interpolate vs mpl griddata

【英文标题】：differences scipy interpolate vs mpl griddata

【发布时间】：2021-12-31 22:15:36

【问题描述】：

我差点把头发扯下来，真的希望有人能在这里帮助我。

我需要将一个脚本从 python 2 转换为 python 3，它是一个简单的脚本，它接受坐标点x、y，以及这些点的值z。

z 在网格上插值，然后绘制。 python 2脚本中的插值目前正在使用from matplotlib.mlab import griddata

但是，python 3 中不存在 mlab griddata。所以我认为我们应该使用 scipy.interpolate 作为替代品。

问题是，它给了我非常奇怪的结果。

最近邻比较

Mpl griddata With interp='nn' 给我：

scipy interpolate using method='nearest' 给了我

这是最重要的，因为这是我需要的结果，但结果却如此不同！

我尝试了其他参数看看是否仍然存在

线性比较

带有interp='linear'的mpl griddata给了我

scipy interpolate with method='linear' 给了我

线性显示相同的结果，但我不在乎线性。

三次比较

mpl griddata 没有三次，但是使用 scipy interpolate 的结果非常奇怪。

数据

import numpy as np
# points
x = np.array([31132.71118116, 10763.66383076, 29340.62119857,  4025.2544491 ,
       19158.87683925, 36584.96725821, 17335.28090098, 27279.80878719,
        5893.32833709, 36392.22873482, 22350.16973122, 40235.86525991,
       19844.57893466, 11245.50791534, 17103.62528354, 29944.77964486,
       34021.92540595, 44485.36307614,  8797.36817447, 24733.44616607,
       30628.62812172, 27227.91858716, 26221.60497488, 27987.74985745,
       14366.37775758, 32035.24328142, 29779.84095199, 42821.14608703,
       42229.95963477, 22592.94483609, 26362.45107434, 22161.13844494,
       21562.53974235, 40784.42626907, 14195.87932099, 25628.56490406,
       19212.62065784, 28354.69294259, 34299.91259166, 28276.85653059,
       13291.49360218, 64014.88912569,     0.        , 64014.88912569,
           0.        ])
    
y = np.array([1.61640041e+04, 1.18226221e+04, 1.66496799e+04, 1.60268291e+04,
       1.47533260e+04, 1.72743862e+04, 2.58461610e+04, 1.11997818e+04,
       1.94747705e+04, 2.81559903e+04, 2.85786579e+04, 2.16418047e+04,
       2.58684064e+04, 2.17474690e+04, 3.21398453e+04, 2.13563269e+04,
       2.12339790e+04, 2.42537633e+04, 1.89242092e+04, 2.45410984e+04,
       1.90984612e+04, 2.45058762e+04, 1.76859142e+04, 2.13655953e+04,
       2.62595562e+04, 1.44826845e+04, 2.55328718e+04, 2.97076285e+04,
       1.81975446e+04, 3.27182416e+04, 1.88407910e+04, 1.58599943e+04,
       2.02514897e+04, 2.42723003e+04, 1.76265941e+04, 1.60045845e+04,
       2.03274941e+04, 1.67609034e+04, 1.74986867e+04, 1.78898244e+04,
       3.21546756e+04, 9.55042196e-08, 9.55042196e-08, 4.04414440e+04,
       4.04414440e+04])
    
z = np.array([0. , 0. , 0. , 0. , 0. , 0. , 0. , 0. , 0.6, 0. , 0. , 0. , 0. ,
       0. , 0. , 0. , 0. , 0. , 0. , 0. , 0. , 0. , 0. , 0. , 0. , 0. ,
       0. , 0. , 0. , 0. , 0. , 0. , 0. , 0. , 0. , 0. , 0. , 0. , 0. ,
       0. , 0. , 0. , 0. , 0. , 0. ])
    
min_grid_val_x = 0
max_grid_val_x = 64014.88912569069

min_grid_val_y = 9.550421964377165e-08
max_grid_val_y = 40441.443993242734
    
# set up a square grid with the same extents as our measured data
numcols, numrows = 1000, 1000
xi = np.linspace(min_grid_val_x, max_grid_val_x, numcols)
yi = np.linspace(min_grid_val_y, max_grid_val_y, numrows)
xi, yi = np.meshgrid(xi, yi)

其他代码

import numpy as np
import pandas as pd
from mpl_toolkits.basemap import Basemap
import matplotlib.pyplot as plt
import matplotlib.colors as mc
import matplotlib.patches as mpatches
from matplotlib.colors import ListedColormap
from matplotlib.colors import Normalize
import math

MODE == 'mpl'
if MODE == 'mpl':
    from matplotlib.mlab import griddata
    zi = griddata(x, y, z, xi, yi, interp='nn')
else:
    from scipy.interpolate import griddata
    points = np.array([[x[i],y[i]] for i in range(len(x))])
    zi = griddata(points, z, (xi, yi), method='cubic',fill_value=0)
    
min_val = math.floor(z.min())
max_val = math.ceil(z.max())
resolutions = [0.1, 0.2, 0.5, 1, 1.5, 2, 3, 5, 10, 
               15, 20, 30, 40, 50, 60, 70, 80]
    
max_of_Z = z.max()
if (max_of_Z==0):
    levels = np.arange(min, min + (0.1 * 12), 0.1)
else:
    hit = False
    for res in resolutions:
        condition = res*12
        if condition > z.max():
            print("Using ".format(res))
            levels = np.arange(min_val, max_val + condition, res)
            hit = True
            break
    if not hit:
        res = 90
        print("Using ".format(res))
        condition = res*12
        levels = np.arange(min_val, max_val + condition, res)
    
norm = mc.BoundaryNorm(levels, len(levels)-1)

cmapV=ListedColormap([[0.73,0.90,0.97],
[0.66,0.87,0.97],
[0.57,0.82,0.95],
[0.49,0.76,0.91],
[0.40,0.69,0.87],
[0.32,0.62,0.83],
[0.26,0.53,0.77],
[0.20,0.44,0.71],
[0.14,0.34,0.64],
[0.13,0.29,0.56],
[0.12,0.23,0.47],
[0.11,0.17,0.38]])

# define map extent
lllat=1.1497
urlat=1.5133
lllon=103.5822
urlon=104.1579
# set up plot
plt.clf()
fig = plt.figure(figsize=(13, 6))
ax = fig.add_subplot(111, facecolor='w', frame_on=False)

# Set up Basemap instance
m = Basemap(
    projection = 'merc',
    llcrnrlon = lllon, llcrnrlat = lllat, urcrnrlon = urlon, urcrnrlat = urlat,
    resolution='h')

# contour plot
con = m.contourf(xi, yi, zi, zorder=1, alpha=None, cmap=cmapV, levels=levels, norm=norm)

【参考方案1】：

根据STOQS 的问题Github 页面上的this discussion，最接近旧Matplotlib 的griddata 默认算法，即自然邻居，是使用scipy.interpolate.griddata 获得的与method='cubic' 和rescale=True。

也就是说，如果您发布的数据代表了您的实际问题，那么您的图表都没有洞察力，因为您不应该从单个数据点 (x=5893.32833709, y=19474.7705, z=0.6) 进行推断，而所有其他数据点都有一个 z纵坐标全等于零。

【讨论】：

嘿，感谢您的回复！我以前看过那个帖子，它对我也不起作用。尝试griddata(points, z, (xi, yi), method='cubic',fill_value=0, rescale=True) 给了我与问题中最后一个情节几乎完全相同的情节。如果它只给出左上角的区域（即大多数点为 0），我会接受这个图。是的，这是真实数据，将是一种常见情况。这种情况下的预期结果是理想情况下的第一个图 (NN)

@Wboy ①如果你在Q中提到你已经看过那个问题，我可能不会浪费时间回答②当你的数据有结构时，插值结果是明智的，尽管有算法;相反……

抱歉浪费您的时间。我正在寻找一种在 python 3 中复制 mpl 的旧 griddata 自然邻居插值的方法。