翻译: 4.4. 模型选择Model Selection欠拟合Underfitting和过拟合Overfitting pytorch

Posted 2022-04-28 AI架构师易筋

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了翻译: 4.4. 模型选择Model Selection欠拟合Underfitting和过拟合Overfitting pytorch相关的知识，希望对你有一定的参考价值。

作为机器学习科学家，我们的目标是发现模式。但是我们怎么能确定我们真的发现了一个普遍的模式，而不是简单地记住我们的数据呢？例如，假设我们想在将患者与其痴呆状态联系起来的遗传标记中寻找模式，其中标签是从集合中提取的dementia, mild cognitive impairment, healthy . 因为每个人的基因唯一地识别他们（忽略相同的兄弟姐妹），所以可以记住整个数据集。

我们不希望我们的模型说“那是 Bob！我记得他！他得了老年痴呆症！” 原因很简单。以后我们部署模型的时候，会遇到模型从来没有见过的病人。只有当我们的模型真正发现了一般模式时，我们的预测才会有用。

更正式地概括一下，我们的目标是发现捕捉我们训练集的基础人群中规律性的模式。如果我们在这方面取得成功，那么即使是我们以前从未遇到过的个人，我们也可以成功地评估风险。这个问题——如何发现泛化的模式——是机器学习的基本问题。

危险在于，当我们训练模型时，我们只能访问一小部分数据。最大的公共图像数据集包含大约一百万张图像。更多的时候，我们必须从数千或数万个数据示例中学习。在大型医院系统中，我们可能会访问数十万份医疗记录。在处理有限样本时，我们冒着发现明显关联的风险，当我们收集更多数据时，这些关联最终无法成立。

将训练数据拟合得比我们拟合底层分布更紧密的现象称为过拟合，而用于对抗过拟合的技术称为正则化。在前面的部分中，您可能在试验 Fashion-MNIST 数据集时观察到了这种效果。如果您在实验期间更改了模型结构或超参数，您可能已经注意到，如果有足够的神经元、层和训练 epoch，模型最终可以在训练集上达到完美的准确度，即使测试数据的准确度下降。

4.4.1 训练误差和泛化误差

为了更正式地讨论这种现象，我们需要区分训练误差和泛化误差。训练误差是我们的模型在训练数据集上计算的误差，而泛化误差是我们模型误差的期望值，如果我们将其应用于从与原始样本相同的基础数据分布中提取的无限附加数据示例流.

问题是，我们永远无法准确计算泛化误差。那是因为无限数据流是一个虚构的对象。在实践中，我们必须通过将我们的模型应用于独立测试集来估计泛化误差，该测试集由从我们的训练集中保留的随机选择的数据示例构成。

以下三个思想实验将有助于更好地说明这种情况。考虑一个试图准备期末考试的大学生。勤奋的学生将努力练习并使用往年的考试测试他的能力。尽管如此，在过去的考试中表现出色并不能保证他在重要的时候会表现出色。例如，学生可能会尝试通过死记硬背考试问题的答案来准备。这需要学生记住很多东西。她甚至可以完美地记住过去考试的答案。另一个学生可能会尝试理解给出某些答案的原因来准备。在大多数情况下，后一个学生会做得更好。

同样，考虑一个简单地使用查找表来回答问题的模型。如果允许的输入集是离散的并且相当小，那么在查看许多训练示例之后，这种方法可能会表现良好。当面对从未见过的例子时，这个模型仍然没有比随机猜测更好的能力。实际上，输入空间太大而无法记住与每个可能的输入相对应的答案。例如，考虑黑白28x28图片。如果每个像素可以取一个256灰度值，则有
257^784可能的图像。这意味着低分辨率灰度缩略图大小的图像比宇宙中的原子数量要多得多。即使我们能遇到这样的数据，我们也永远无法存储查找表。

最后，考虑尝试根据一些可能可用的上下文特征对抛硬币的结果（第 0 类：正面，第 1 类：反面）进行分类的问题。假设硬币是公平的。不管我们想出什么算法，泛化误差总是1/2. 然而，对于大多数算法，我们应该期望我们的训练误差要低得多，这取决于抽签的运气，即使我们没有任何特征！考虑数据集 0, 1, 1, 1, 0, 1。我们的无特征算法将不得不依赖于总是预测多数类，从我们有限的样本来看，它似乎是1。在这种情况下，总是预测第 1 类的模型将产生1/3，比我们的泛化错误要好得多。随着数据量的增加，正面的比例将显着偏离的概率1/2减少，我们的训练误差将与泛化误差相匹配。

4.4.1.1。统计学习理论

由于泛化是机器学习中的基本问题，因此您可能不会对许多数学家和理论家毕生致力于发展形式化理论来描述这一现象感到惊讶。在他们的同名定理中，Glivenko 和 Cantelli 导出了训练误差收敛到泛化误差的速率。在一系列开创性的论文中， Vapnik 和 Chervonenkis 将这一理论扩展到更一般的函数类别。这项工作奠定了统计学习理论的基础。

在标准的监督学习设置中，直到现在我们已经解决并将在本书的大部分内容中坚持使用，我们假设训练数据和测试数据都是独立于相同的分布绘制的。这通常称为iid 假设，这意味着对我们的数据进行采样的过程没有内存。换言之，抽取的第二个样本和抽取的第三个样本的相关性并不比抽取的第二个样本和百万分之二样本的相关性高。

成为一名优秀的机器学习科学家需要批判性地思考，你应该已经在这个假设中戳破洞，提出假设失败的常见案例。如果我们根据从 UCSF 医学中心的患者收集的数据训练死亡风险预测器，并将其应用于马萨诸塞州总医院的患者会怎样？这些分布根本不完全相同。此外，平局可能在时间上相关。如果我们对推文的主题进行分类怎么办？新闻周期会在讨论的主题中产生时间依赖性，违反任何独立性假设。

有时我们可以通过轻微违反 iid 假设而侥幸逃脱，并且我们的模型将继续工作得非常好。毕竟，几乎每个现实世界的应用程序都至少涉及到对 iid 假设的一些轻微违反，但我们有许多有用的工具可用于各种应用程序，例如人脸识别、语音识别和语言翻译。

其他违规行为肯定会造成麻烦。例如，想象一下，如果我们尝试通过专门针对大学生进行培训来训练人脸识别系统，然后希望将其部署为监测疗养院人群中老年病学的工具。这不太可能奏效，因为大学生往往看起来与老年人有很大不同。

在随后的章节中，我们将讨论因违反 iid 假设而引起的问题。就目前而言，即使将 iid 假设视为理所当然，理解泛化也是一个艰巨的问题。此外，阐明可能解释为什么深度神经网络能像它们一样泛化的精确理论基础继续困扰着学习理论中最伟大的思想家。

当我们训练我们的模型时，我们会尝试寻找一个尽可能适合训练数据的函数。如果该函数非常灵活，以至于它可以像捕捉真实关联一样容易地捕捉到虚假模式，那么它可能会执行得太好，而不会产生一个可以很好地泛化到看不见的数据的模型。这正是我们想要避免或至少要控制的。深度学习中的许多技术都是旨在防止过度拟合的启发式方法和技巧。

4.4.1.2。模型复杂度

当我们有简单的模型和丰富的数据时，我们期望泛化误差类似于训练误差。当我们使用更复杂的模型和更少的示例时，我们预计训练误差会下降，但泛化差距会扩大。究竟是什么构成了模型复杂性是一个复杂的问题。许多因素决定了模型是否能很好地泛化。例如，具有更多参数的模型可能被认为更复杂。参数可以采用更广泛值的模型可能更复杂。通常对于神经网络，我们认为需要更多训练迭代的模型更复杂，而需要提前停止（更少训练迭代）的模型不太复杂。

比较不同模型类（例如决策树与神经网络）的成员之间的复杂性可能很困难。就目前而言，一个简单的经验法则非常有用：一个可以轻松解释任意事实的模型是统计学家认为复杂的模型，而一个表达能力有限但仍能很好地解释数据的模型可能更接近事实. 在哲学上，这与波普尔的科学理论可证伪性标准密切相关：如果一个理论适合数据并且有特定的测试可以用来反驳它，那么它就是好的理论。这很重要，因为所有统计估计都是事后的，即我们在观察事实后进行估计，因此容易受到相关谬误的影响。现在，我们将把理念放在一边，坚持更具体的问题。

在本节中，为了给您一些直觉，我们将重点关注一些往往会影响模型类的泛化性的因素：

可调参数的数量。当可调参数的数量（有时称为自由度）很大时，模型往往更容易过度拟合。
参数采用的值。当权重可以取更大范围的值时，模型更容易受到过度拟合的影响。
训练示例的数量。即使您的模型很简单，也很容易过度拟合仅包含一两个示例的数据集。但是用数百万个例子过拟合数据集需要一个非常灵活的模型。

4.4.2. 模型选择

在机器学习中，我们通常在评估几个候选模型后选择我们的最终模型。这个过程称为模型选择。有时，要比较的模型本质上是完全不同的（例如，决策树与线性模型）。在其他时候，我们会比较已使用不同超参数设置训练的同一类模型的成员。

例如，对于 MLP，我们可能希望比较具有不同隐藏层数量、不同隐藏单元数量以及应用于每个隐藏层的激活函数的各种选择的模型。为了确定我们的候选模型中最好的，我们通常会使用验证数据集。

4.4.2.1 验证数据集

原则上，在我们选择了所有超参数之前，我们不应该接触我们的测试集。如果我们在模型选择过程中使用测试数据，我们可能会过度拟合测试数据。那么我们就会遇到严重的麻烦。如果我们过度拟合我们的训练数据，总会有对测试数据的评估来保持我们的诚实。但是如果我们过度拟合测试数据，我们怎么知道呢？

因此，我们永远不应该依赖测试数据进行模型选择。然而，我们也不能仅仅依靠训练数据进行模型选择，因为我们无法估计用于训练模型的数据的泛化误差。

在实际应用中，画面变得更加模糊。虽然理想情况下我们只会接触一次测试数据，以评估最好的模型或将少量模型相互比较，但现实世界的测试数据很少会在一次使用后被丢弃。我们很少能为每一轮实验提供一个新的测试集。

解决这个问题的常见做法是将我们的数据分成三种方式，除了训练和测试数据集之外，还包含一个验证数据集（或验证集）。结果是一种模糊的实践，验证和测试数据之间的界限令人担忧地模棱两可。除非另有明确说明，否则在本书的实验中，我们实际上是在使用应该被正确称为训练数据和验证数据的东西，没有真正的测试集。因此，本书每个实验报告的准确度实际上是验证准确度，而不是真正的测试集准确度。

4.4.2.2. K-折叠交叉验证

当训练数据稀缺时，我们甚至可能无法承受足够的数据来构成适当的验证集。解决此问题的一种流行方法是采用K-折叠交叉验证。在这里，原始的训练数据被分成K 不重叠的子集。然后执行模型训练和验证K次，每次训练K-1子集并在不同的子集（该轮中未用于训练的子集）上进行验证。最后，通过对来自K实验。

4.4.3. 欠拟合还是过拟合？ Underfitting or Overfitting?

当我们比较训练和验证错误时，我们要注意两种常见情况。首先，我们要注意训练错误和验证错误都很大但它们之间有一点差距的情况。如果模型无法减少训练错误，这可能意味着我们的模型太简单（即表达力不足）而无法捕捉我们试图建模的模式。此外，由于我们的训练和验证错误之间的泛化差距很小，我们有理由相信我们可以摆脱更复杂的模型。这种现象被称为欠拟合。

另一方面，正如我们上面所讨论的，我们要注意训练误差明显低于验证误差的情况，这表明严重的过拟合。请注意，过度拟合并不总是一件坏事。尤其是深度学习，众所周知，最好的预测模型在训练数据上的表现通常比在保留数据上的表现要好得多。最终，我们通常更关心验证错误，而不是训练和验证错误之间的差距。

我们是过拟合还是欠拟合取决于模型的复杂性和可用训练数据集的大小，这两个主题将在下面讨论。

4.4.3.1 模型复杂度

为了说明关于过度拟合和模型复杂性的一些经典直觉，我们给出了一个使用多项式的例子。给定包含单个特征的训练数据x和相应的实值标签y，我们试图找到度的多项式d.

高阶多项式函数比低阶多项式函数更复杂，因为高阶多项式的参数更多，模型函数的选择范围更广。固定训练数据集，相对于低阶多项式，高阶多项式函数应始终实现较低（最坏情况下相等）的训练误差。事实上，只要数据示例每个都有不同的值x，度数等于数据样本数的多项式函数可以完美拟合训练集。我们在图 4.4.1中可视化多项式次数和欠拟合与过拟合之间的关系。

4.4.3.2 数据集大小

要记住的另一个重要考虑因素是数据集大小。修复我们的模型，我们在训练数据集中拥有的样本越少，我们就越有可能（也更严重）遇到过拟合。随着我们增加训练数据量，泛化误差通常会降低。此外，一般来说，更多的数据永远不会受到伤害。对于固定的任务和数据分布，模型复杂性和数据集大小之间通常存在关系。给定更多数据，我们可能会尝试拟合更复杂的模型。如果没有足够的数据，更简单的模型可能更难被击败。对于许多任务，只有在有数千个训练示例可用时，深度学习才能胜过线性模型。深度学习目前的成功部分归功于互联网公司、廉价存储.

4.4.4. 多项式回归

我们现在可以通过将多项式拟合到数据来交互式地探索这些概念。

import math
import numpy as np
import torch
from torch import nn
from d2l import torch as d2l

4.4.4.1。生成数据集

首先我们需要数据。给定x，我们将使用以下三次多项式在训练和测试数据上生成标签：

max_degree = 20  # Maximum degree of the polynomial
n_train, n_test = 100, 100  # Training and test dataset sizes
true_w = np.zeros(max_degree)  # Allocate lots of empty space
true_w[0:4] = np.array([5, 1.2, -3.4, 5.6])

features = np.random.normal(size=(n_train + n_test, 1))
np.random.shuffle(features)
poly_features = np.power(features, np.arange(max_degree).reshape(1, -1))
for i in range(max_degree):
    poly_features[:, i] /= math.gamma(i + 1)  # `gamma(n)` = (n-1)!
# Shape of `labels`: (`n_train` + `n_test`,)
labels = np.dot(poly_features, true_w)
labels += np.random.normal(scale=0.1, size=labels.shape)

# Convert from NumPy ndarrays to tensors
true_w, features, poly_features, labels = [torch.tensor(x, dtype=
    torch.float32) for x in [true_w, features, poly_features, labels]]

features[:2], poly_features[:2, :], labels[:2]

(tensor([[ 0.4015],
         [-0.2346]]),
 tensor([[ 1.0000e+00,  4.0154e-01,  8.0618e-02,  1.0791e-02,  1.0832e-03,
           8.6992e-05,  5.8218e-06,  3.3396e-07,  1.6762e-08,  7.4787e-10,
           3.0030e-11,  1.0962e-12,  3.6681e-14,  1.1330e-15,  3.2497e-17,
           8.6992e-19,  2.1832e-20,  5.1567e-22,  1.1504e-23,  2.4312e-25],
         [ 1.0000e+00, -2.3458e-01,  2.7513e-02, -2.1513e-03,  1.2616e-04,
          -5.9190e-06,  2.3141e-07, -7.7548e-09,  2.2739e-10, -5.9266e-12,
           1.3903e-13, -2.9647e-15,  5.7955e-17, -1.0458e-18,  1.7522e-20,
          -2.7402e-22,  4.0174e-24, -5.5435e-26,  7.2244e-28, -8.9193e-30]]),
 tensor([5.2693, 4.6050]))

4.4.4.2 训练和测试模型

让我们首先实现一个函数来评估给定数据集的损失。

def evaluate_loss(net, data_iter, loss):  #@save
    """Evaluate the loss of a model on the given dataset."""
    metric = d2l.Accumulator(2)  # Sum of losses, no. of examples
    for X, y in data_iter:
        out = net(X)
        y = y.reshape(out.shape)
        l = loss(out, y)
        metric.add(l.sum(), l.numel())
    return metric[0] / metric[1]

现在定义训练函数。

def train(train_features, test_features, train_labels, test_labels,
          num_epochs=400):
    loss = nn.MSELoss(reduction='none')
    input_shape = train_features.shape[-1]
    # Switch off the bias since we already catered for it in the polynomial
    # features
    net = nn.Sequential(nn.Linear(input_shape, 1, bias=False))
    batch_size = min(10, train_labels.shape[0])
    train_iter = d2l.load_array((train_features, train_labels.reshape(-1,1)),
                                batch_size)
    test_iter = d2l.load_array((test_features, test_labels.reshape(-1,1)),
                               batch_size, is_train=False)
    trainer = torch.optim.SGD(net.parameters(), lr=0.01)
    animator = d2l.Animator(xlabel='epoch', ylabel='loss', yscale='log',
                            xlim=[1, num_epochs], ylim=[1e-3, 1e2],
                            legend=['train', 'test'])
    for epoch in range(num_epochs):
        d2l.train_epoch_ch3(net, train_iter, loss, trainer)
        if epoch == 0 or (epoch + 1) % 20 == 0:
            animator.add(epoch + 1, (evaluate_loss(net, train_iter, loss),
                                     evaluate_loss(net, test_iter, loss)))
    print('weight:', net[0].weight.data.numpy())

4.4.4.3 三阶多项式函数拟合（正常）

我们将首先使用三阶多项式函数，它与数据生成函数的阶数相同。结果表明，该模型的训练和测试损失均能有效降低。学习到的模型参数也接近真实值w = [5, 1.2, -3.4, 5.6] .

# Pick the first four dimensions, i.e., 1, x, x^2/2!, x^3/3! from the
# polynomial features
train(poly_features[:n_train, :4], poly_features[n_train:, :4],
      labels[:n_train], labels[n_train:])

weight: [[ 4.999099   1.2192062 -3.377857   5.5528784]]

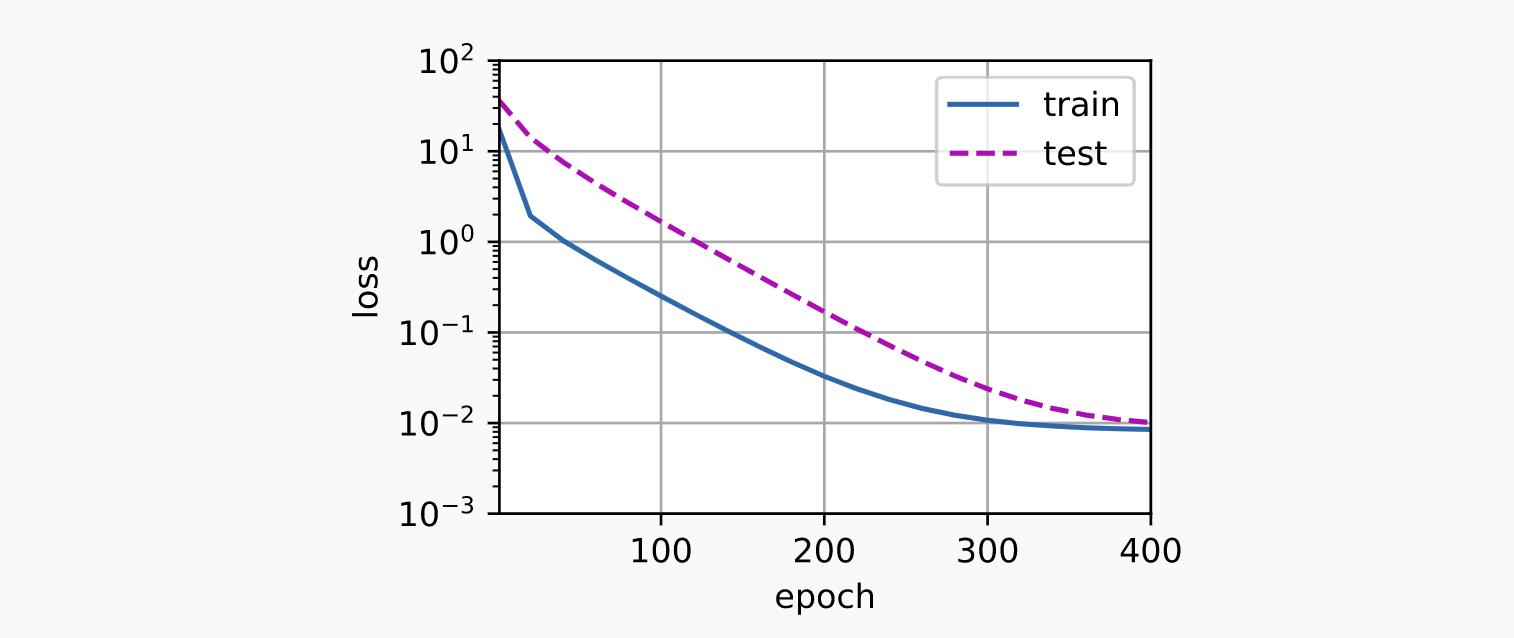
4.4.4.4 线性函数拟合（欠拟合）

让我们再看一下线性函数拟合。在早期 epoch 下降之后，进一步降低该模型的训练损失变得困难。在最后一个 epoch 迭代完成后，训练损失仍然很高。当用于拟合非线性模式（如这里的三阶多项式函数）时，线性模型容易欠拟合。

# Pick the first two dimensions, i.e., 1, x, from the polynomial features
train(poly_features[:n_train, :2], poly_features[n_train:, :2],
      labels[:n_train], labels[n_train:])

weight: [[3.7911081 2.5833387]]

4.4.4.5 高阶多项式函数拟合（过拟合）

现在让我们尝试使用过高次数的多项式来训练模型。在这里，没有足够的数据来了解更高次系数的值应该接近于零。因此，我们过于复杂的模型非常容易受到训练数据中噪声的影响。虽然可以有效减少训练损失，但测试损失仍然高得多。它表明复杂模型过拟合数据。

# Pick all the dimensions from the polynomial features
train(poly_features[:n_train, :], poly_features[n_train:, :],
      labels[:n_train], labels[n_train:], num_epochs=1500)

weight: [[ 5.0019913   1.2659464  -3.3324203   5.2160134  -0.31978676  1.2983036
   0.01977059  0.20886001 -0.02627637 -0.17851575 -0.16669305 -0.2156814
  -0.09898872 -0.18689805  0.05609591 -0.10168056 -0.1683235   0.22086866
  -0.16249742 -0.05473528]]

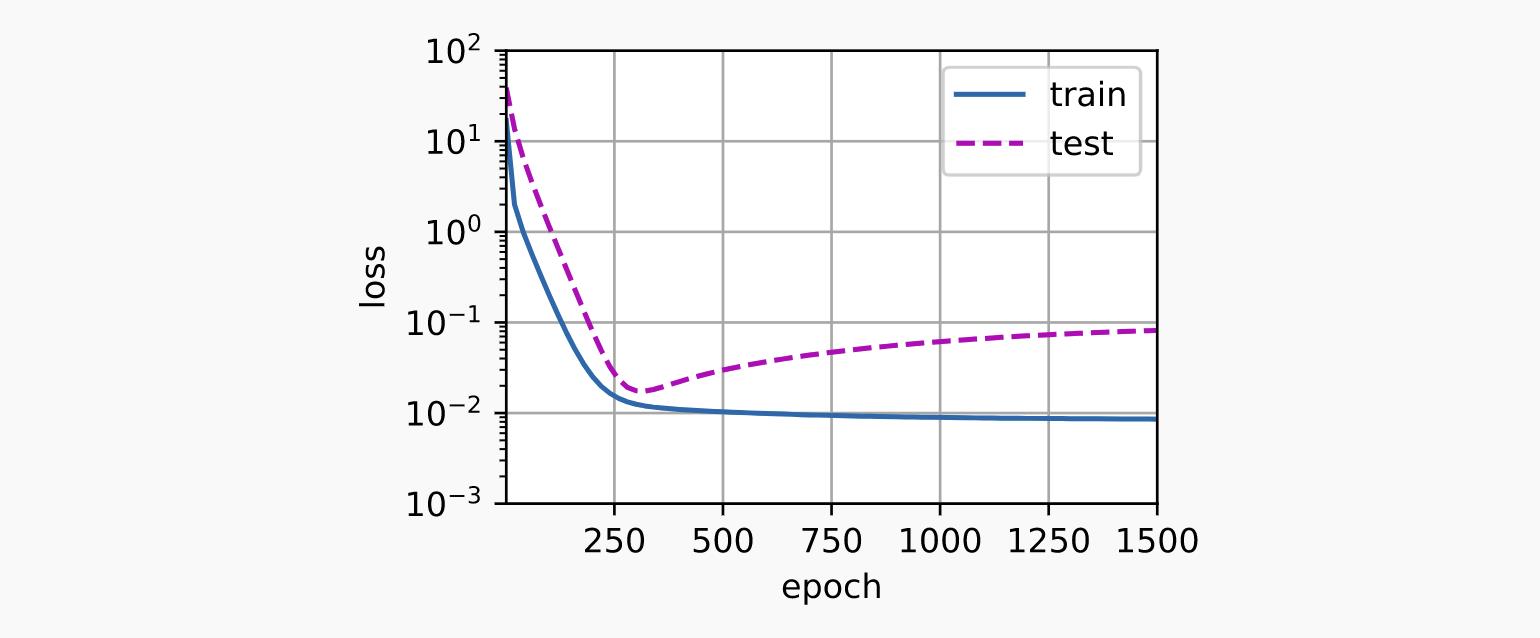
在随后的章节中，我们将继续讨论过拟合问题和处理它们的方法，例如权重衰减和 dropout。