七大常见排序，你究竟懂几个？（下）
Posted 拼命阿紫
tags:
篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了七大常见排序，你究竟懂几个？（下）相关的知识，希望对你有一定的参考价值。
一百个人眼中一百个我，我既是天使
又是恶魔
生活的路上总会遇到形形色色的人
他们对我们的评价都各有千秋
就像优秀的人看到看到努力的人，会感觉他很自律 很拼
而一些一无所有还想着躺平的人，会感觉他很卷 很作
我们要做的并不是因为那些躺平人的眼光而改变自我的目标
而是悄悄的努力成为别人的梦想
1.冒泡排序
2.快速排序
3.归并排序
1、冒泡排序
升序排序：
升序：每一趟比较，都会让对比的数中的最大数进行归位
降序：每一趟比较，都会让对比的数中的最小数进行归位
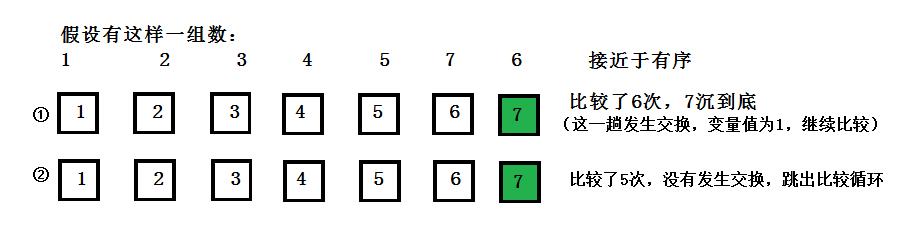
思考：要是本就有序或者接近有序，还要对比n-1趟吗？（要是这样还要对比n-1趟也太麻烦了吧！）
解决办法： 我们可以用一个变量记录，要是一趟中没有进行交换，就默认为0，要是发生交换了就为1。然后判断这个变量是否为0，要是为0跳出比较循环，否则继续执行循环比较。
代码：
#define _CRT_SECURE_NO_WARNINGS 1
#include<stdio.h>
//交换
void Swap(int* p1, int* p2)
int tmp = *p1;
*p1 = *p2;
*p2 = tmp;
//冒泡排序
void BubbleSort(int* a, int n)
for (int j = 0; j < n; j++)
int exchange = 0;
for (int i = 1; i < n - j; i++)
if (a[i - 1] > a[i])
Swap(&a[i - 1], &a[i]);
exchange = 1;//避免不必要的排序
if (exchange == 0)
break;
void PrintArray(int* a, int n)
for (int i = 0; i < n; i++)
printf("%d ", a[i]);
printf("\\n");
int main()
int a[] = 7, 3, 2, 6, 8, 1, 9;
int size = sizeof(a) / sizeof(int);
BubbleSort(a, size);
PrintArray(a, size);
return 0;
冒泡排序的特性总结：
- 冒泡排序是一种非常容易理解的排序
- 时间复杂度：O(N^2)
- 空间复杂度：O(1)
- 稳定性：稳定
2、快速排序
2.1挖坑法
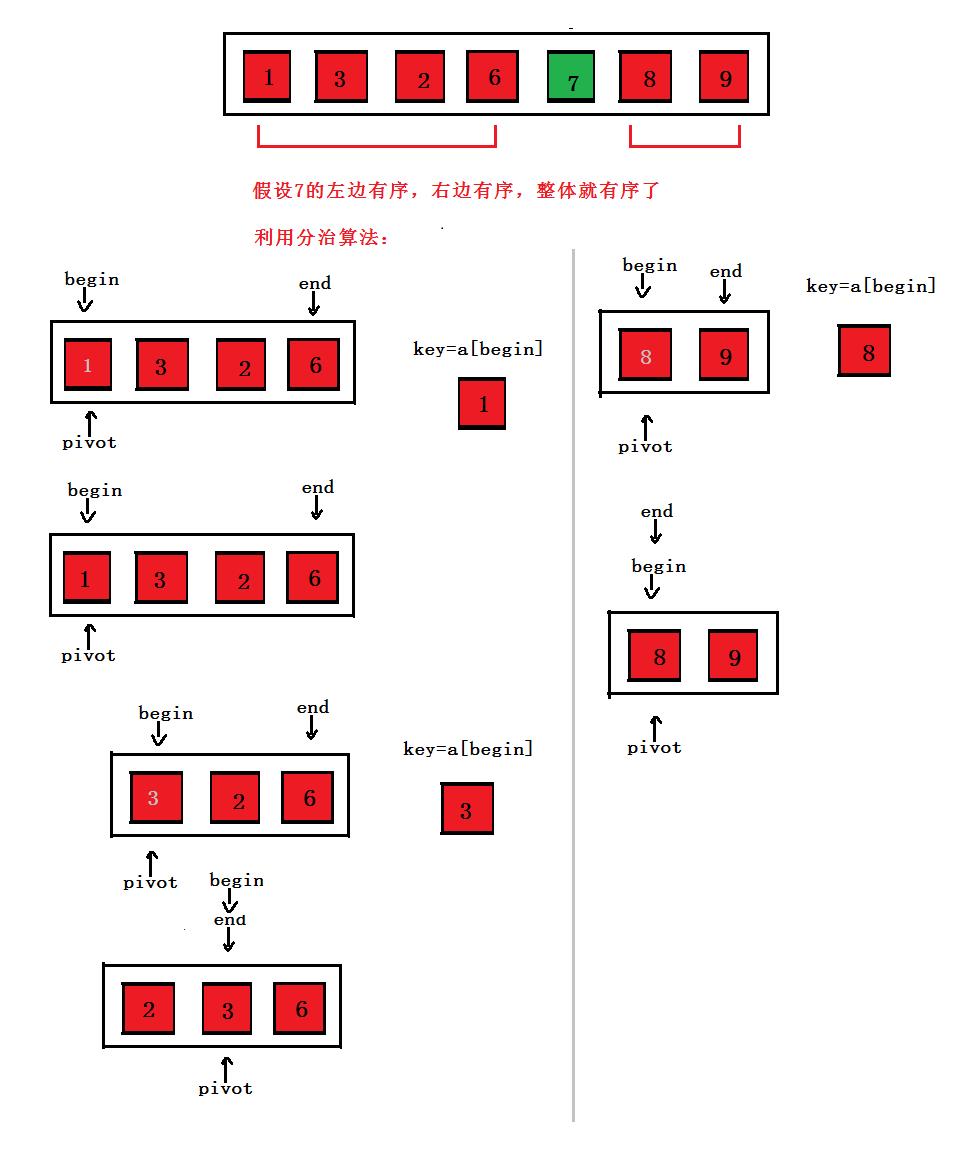
注：一般把第一个或最后一个数当做关键字，向左找比关键字key小的值，向右找比关键字key大的值。
思路：首先把第一个数当做关键字赋值给key，然后第一个数的位置就是一个坑，从end向左找找比关键字小的数，找到之后把他放到坑里，然后它所在的位置变成一个新坑，然后在从begin向右找比关键字大的数放进新坑继续形成一个新坑，依次这样直到end和begin和pivot指向同一个位置把key放进这个地方，这一趟排序会使一个数归位。然后用同样的方式让这个数左边的数有序，右边的数有序，整个数组就有序了。
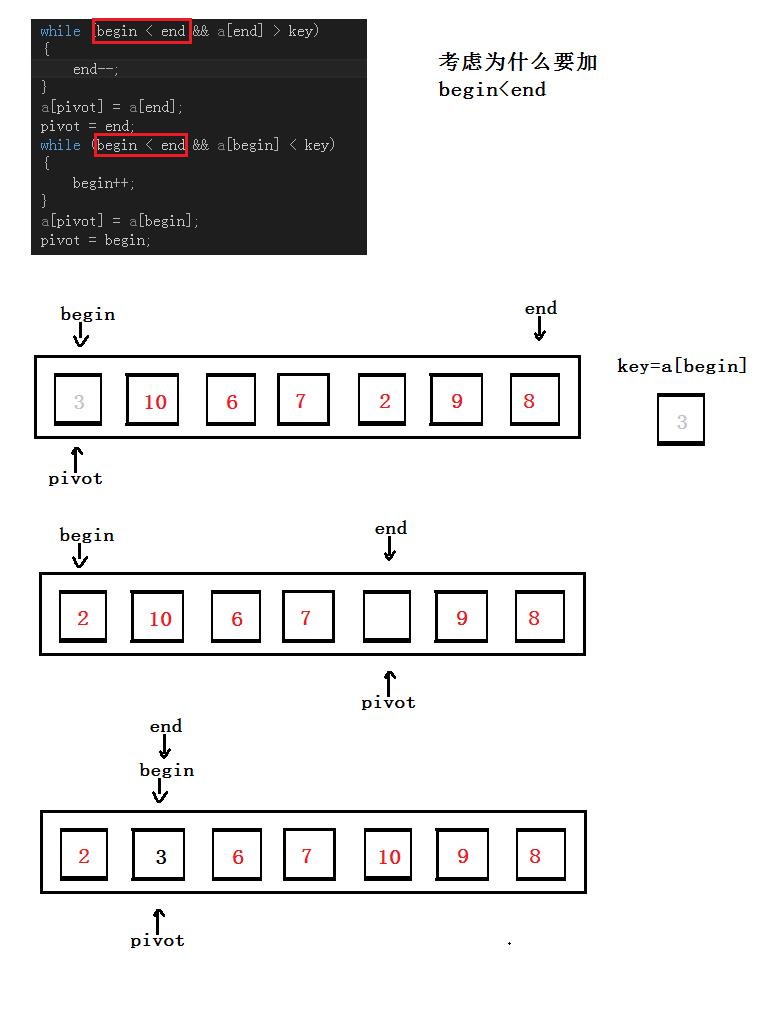
思考：为什么要加begin < end ?
因为当begin = end时，key值也就归位了，然后key前已经小于key值，key后已经大于key值。所以不需要跨越查找。
考虑：快速排序什么情况下最坏了？当它有序时，时间复杂度为O(N^2)。
那我们怎么解决这种问题了？？？
利用三数取中法。
三数取中法思路：对比第一个下标的数和中间下标的数与最后下标的数，返回中间数（不是最大也不是最小）。
#define _CRT_SECURE_NO_WARNINGS 1
#include<stdio.h>
//交换
void Swap(int* p1, int* p2)
int tmp = *p1;
*p1 = *p2;
*p2 = tmp;
//三数取中法
int GetMidIndex(int* a, int left, int right)
int mid = (left + right) >> 1;
if (a[left] < a[mid])
if (a[mid] < a[right])
return mid;
else if (a[left] > a[right])
return left;
else
return right;
else // a[left] > a[mid]
if (a[mid] > a[right])
return mid;
else if (a[left] < a[right])
return left;
else
return right;
//快速排序之挖坑法
void QuickSort(int* a,int left,int right)
if (left >= right)
return;
int index = GetMidIndex(a, left, right);
Swap(&a[left], &a[index]);
int begin = left;
int end = right;
int key = a[begin];
int pivot = begin;
while (begin < end)
while (begin < end && a[end] >= key)
end--;
a[pivot] = a[end];
pivot = end;
while (begin < end && a[begin] <= key)
begin++;
a[pivot] = a[begin];
pivot = begin;
a[pivot] = key;
QuickSort(a, left, pivot - 1);
QuickSort(a, pivot + 1, right);
void PrintArray(int* a, int n)
for (int i = 0; i < n; i++)
printf("%d ", a[i]);
printf("\\n");
int main()
int a[] = 7, 3, 2, 6, 8, 1, 9;
int size = sizeof(a) / sizeof(int);
QuickSort(a, 0, size - 1);
PrintArray(a, size);
return 0;
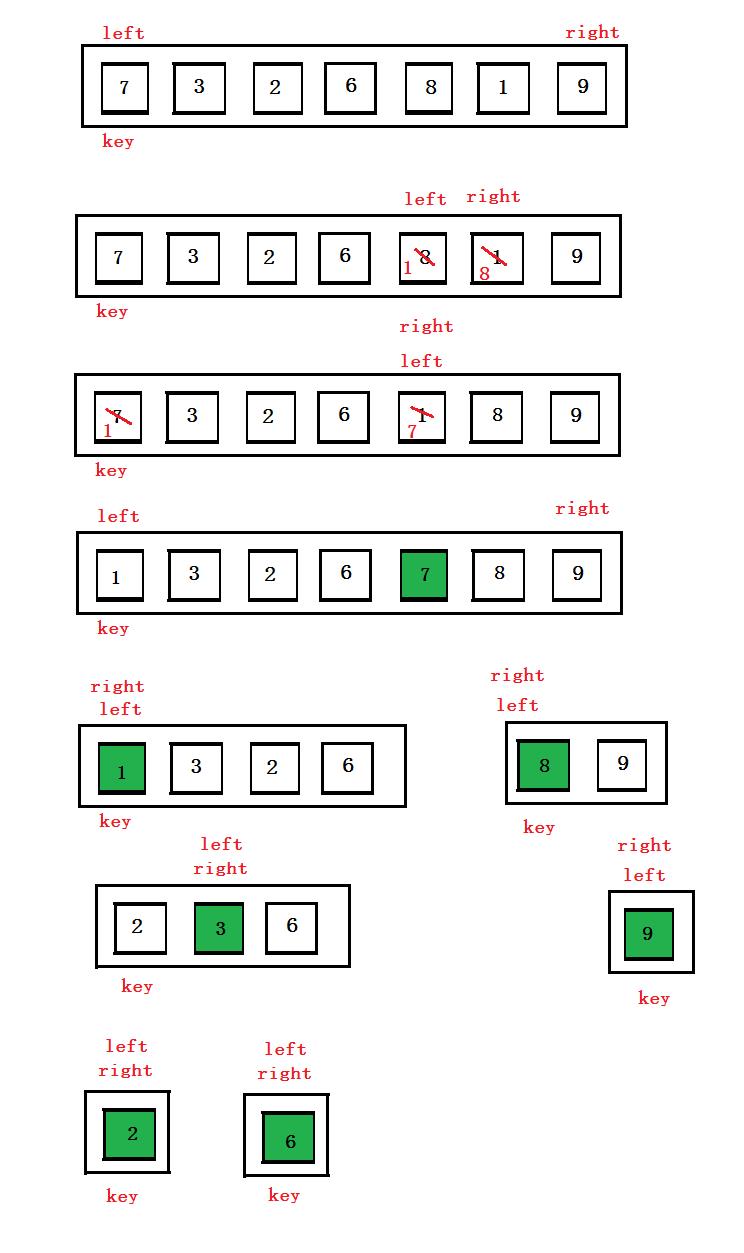
2.2左右指针法
思路：向左找比关键字小的，向右找比关键字大的，找到之后交换
#define _CRT_SECURE_NO_WARNINGS 1
#include<stdio.h>
//交换
void Swap(int* p1, int* p2)
int tmp = *p1;
*p1 = *p2;
*p2 = tmp;
//三数取中法
int GetMidIndex(int* a, int left, int right)
int mid = (left + right) >> 1;
if (a[left] < a[mid])
if (a[mid] < a[right])
return mid;
else if (a[left] > a[right])
return left;
else
return right;
else // a[left] > a[mid]
if (a[mid] > a[right])
return mid;
else if (a[left] < a[right])
return left;
else
return right;
//快速排序之左右指针法
void QuickSort2(int* a, int lefti, int righti)
if (lefti >= righti)
return;
int index = GetMidIndex(a, lefti, righti);
Swap(&a[lefti], &a[index]);
int left = lefti;
int right = righti;
int key = left;
while (left < right)
while (left < right && a[right] >= a[key])
--right;
while (left < right && a[left] <= a[key])
++left;
Swap(&a[left], &a[right]);
Swap(&a[key], &a[left]);
QuickSort2(a, lefti, left-1);
QuickSort2(a, left+1, righti);
void PrintArray(int* a, int n)
for (int i = 0; i < n; i++)
printf("%d ", a[i]);
printf("\\n");
int main()
int a[] = 7, 3, 2, 6, 8, 1, 9;
int size = sizeof(a) / sizeof(int);
QuickSort2(a, 0, size - 1);
PrintArray(a, size);
return 0;
2.3前后指针法
思路：front在前面找比key大的值，当找到了after++，然后交换两个值 （小的往前推，大的往后推）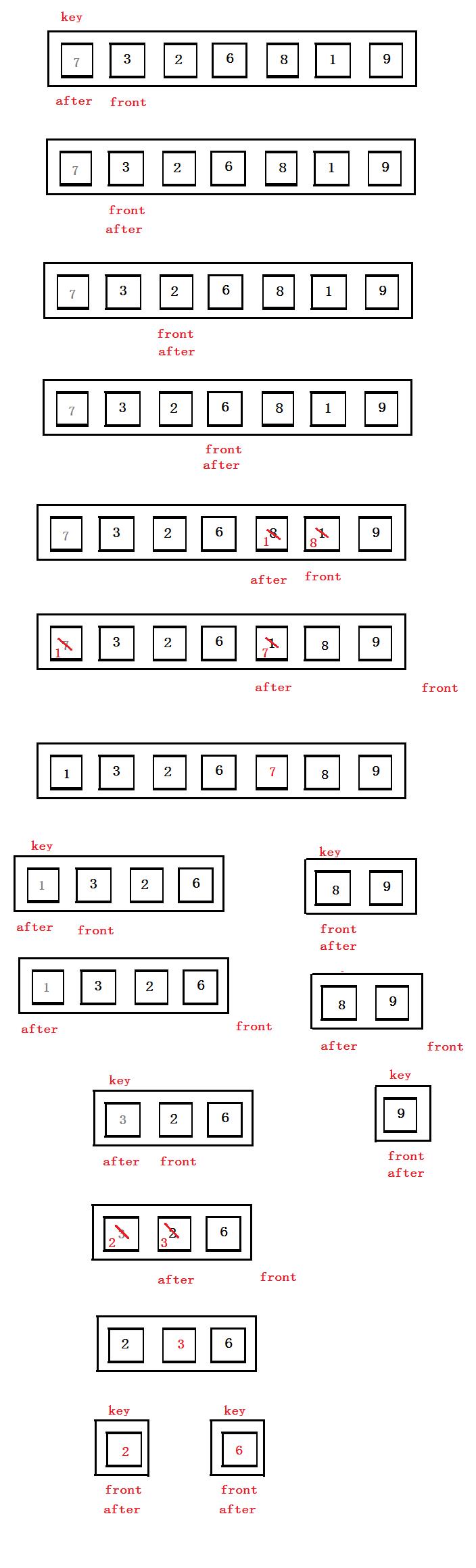
#define _CRT_SECURE_NO_WARNINGS 1
#include<stdio.h>
//交换
void Swap(int* p1, int* p2)
int tmp = *p1;
*p1 = *p2;
*p2 = tmp;
//三数取中法
int GetMidIndex(int* a, int left, int right)
int mid = (left + right) >> 1;
if (a[left] < a[mid])
if (a[mid] < a[right])
return mid;
else if (a[left] > a[right])
return left;
else
return right;
else // a[left] > a[mid]
if (a[mid] > a[right])
return mid;
else if (a[left] < a[right])
return left;
else
return right;
//快速排序之前后指针法
void QuickSort3(int* a, int lefti, int righti)
if (lefti >= righti)
return;
int index = GetMidIndex(a, lefti, righti);
Swap(&a[lefti], &a[index]);
int after = lefti;
int front = lefti + 1;
int key = lefti;
while (front <= righti)
if (a[front] < a[key])
after++;
Swap(&a[front], &a[after]);
front++;
Swap(&a[after], &a[key]);
QuickSort3(a, lefti, after - 1);
QuickSort3(a, after + 1, righti);
void PrintArray(int* a, int n)
for (int i = 0; i < n; i++)
printf("%d ", a[i]);
printf("\\n");
int main()
int a[] = 7, 3, 2, 6, 8, 1, 9;
int size = sizeof(a) / sizeof(int);
QuickSort3(a, 0, size - 1);
PrintArray(a, size);
return 0;
快速排序的特性总结：
- 快速排序整体的综合性能和使用场景都是比较好的，所以才敢叫快速排序
- 时间复杂度：O(N*logN)
- 空间复杂度：O(logN)
- 稳定性：不稳定
3、归并排序
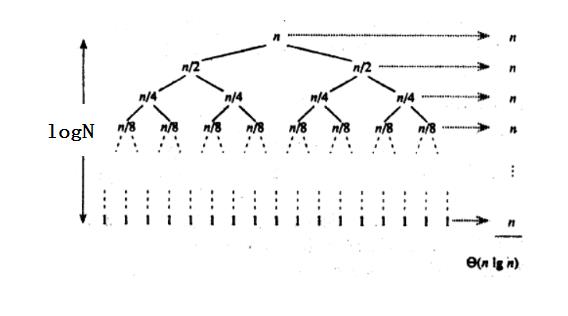
基本思想： 归并排序（MERGE-SORT）是建立在归并操作上的一种有效的排序算法,该算法是采用分治法 （Divide and Conquer）的一个非常典型的应用。将已有序的子序列合并，得到完全有序的序列；即先使每个子序列有序，再使子序列段间有序。若将两个有序表合并成一个有序表，称为二路归并。
#include<stdlib.h>
#include<stdio.h>
//归并排序
void _MergeSort(int* a, int left, int right, int* tmp)
if (left >= right)
return;
int mid = (left + right) >> 1;
// 假设 [left, mid] [mid+1, right]有序，那么我们就可以归并了
_MergeSort(a, left, mid, tmp);
_MergeSort(a, mid + 1, right, tmp);
// 归并
int begin1 = left, end1 = mid;
int begin2 = mid + 1, end2 = right;
int index = left;
while (begin1 <= end1 && begin2 <= end2)
if (a[begin1] < a[begin2])
tmp[index++] = a[begin1++];
else
tmp[index++] = a[begin2++];
while (begin1 <= end1)
tmp[index++] = a[begin1++];
while (begin2 <= end2)
tmp[index++] = a[begin2++];
// 拷贝回去
for (int i = left; i <= right; ++i)
a[i] = tmp[i];
void MergeSort(int* a, int n)
int* tmp = (int*)malloc(sizeof(int)*n);
_MergeSort(a, 0, n - 1, tmp);
free(tmp);
void PrintArray(int* a, int n)
for (int i = 0; i < n; i++)
printf("%d ", a[i]);
printf("\\n");
int main()
MergeSort(a, size - 1);
PrintArray(a, size);
return 0;
归并排序的特性总结：
- 归并的缺点在于需要O(N)的空间复杂度，归并排序的思考更多的是解决在磁盘中的外排序问 题。
- 时间复杂度：O(N*logN)
- 空间复杂度：O(N)
- 稳定性：稳定
排序算法复杂度及稳定性分析
超强干货来袭
云风专访：近40年码龄，通宵达旦的技术人生
以上是关于七大常见排序，你究竟懂几个？（下）的主要内容，如果未能解决你的问题，请参考以下文章