Learning Without Forgetting 笔记及实现
Posted juggle_gap_horse
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了Learning Without Forgetting 笔记及实现相关的知识,希望对你有一定的参考价值。
Learning Without Forgetting
LWF简介
LWF是结合知识蒸馏(KD)避免灾难性遗忘的经典持续学习方法。本质上是通过旧网络指导的输出对在新任务训练的网络参数进行平衡,从而得到在新旧任务网络上都表现较好的性能。
方法对比
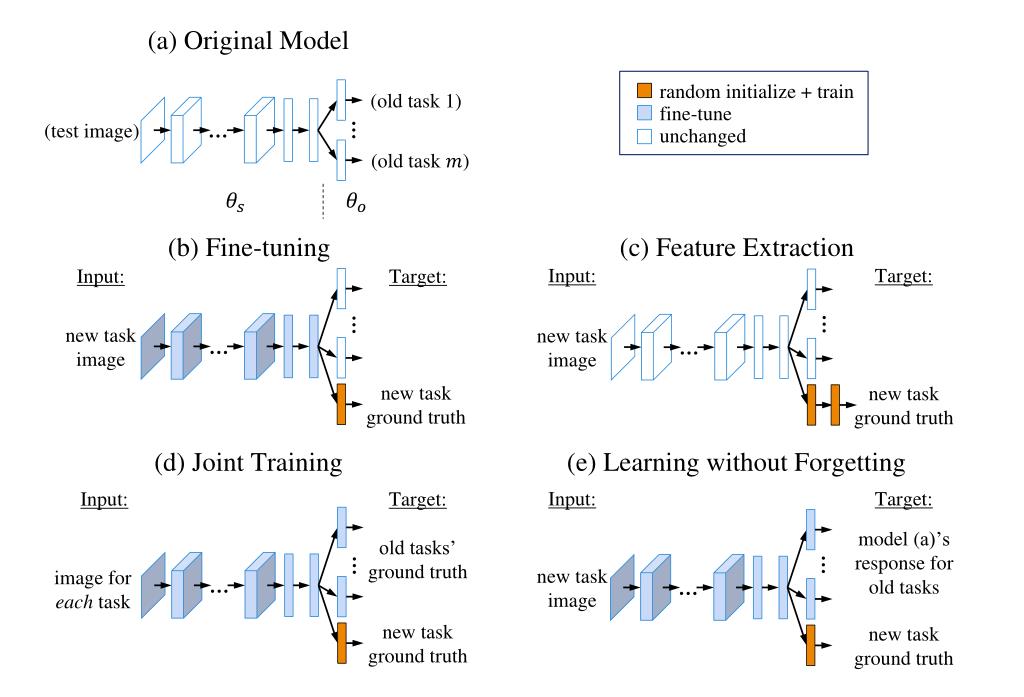
a.从头开始训练
b.微调:在旧任务的网络基础上以较小的学习率学习新任务 另一种意义上的initialization?
c.联合训练:使用所有任务的数据一起训练
d.特征提取:将旧任务的参数固定作为特征提取器,添加新的层训练新任务
LWF算法流程

θ
s
\\theta_s
θs为在old task上pretrained网络CNN的共享参数
θ
o
\\theta_o
θo为每个old task的特定参数(可理解为网络的i最后的classifier head)
(
X
n
,
Y
n
)
(X_n,Y_n)
(Xn,Yn) new task的数据
初始化:
1.将新数据
(
X
n
,
Y
n
)
(X_n,Y_n)
(Xn,Yn) 输入在旧任务pretrained网络中得到一组respond
Y
o
Y_o
Yo
2.将new task对应的classifier head参数随机初始化(加快训练的常见手段)
训练:
Y
o
^
\\hatY_o
Yo^ 为待训练网络CNN 对应old task的输出,最开始
θ
o
\\theta_o
θo=
θ
o
^
\\hat\\theta_o
θo^ ,
θ
s
\\theta_s
θs=
θ
s
^
\\hat\\theta_s
θs^
Y
n
^
\\hatY_n
Yn^ 为待训练网络对应new task的输出,最开始
θ
n
\\theta_n
θn=
θ
n
^
\\hat\\theta_n
θn^ ,
θ
s
\\theta_s
θs=
θ
s
^
\\hat\\theta_s
θs^
优化目标为
θ
s
∗
,
θ
o
∗
,
θ
n
∗
←
argmin
θ
^
s
,
θ
^
o
,
θ
^
n
(
λ
o
L
o
l
d
(
Y
o
,
Y
^
o
)
+
L
n
e
w
(
Y
n
,
Y
^
n
)
+
R
(
θ
^
s
,
θ
^
o
,
θ
^
n
)
)
\\theta_s^*, \\theta_o^*, \\theta_n^* \\leftarrow \\underset\\hat\\theta_s, \\hat\\theta_o, \\hat\\theta_n\\operatornameargmin\\left(\\lambda_o \\mathcalL_o l d\\left(Y_o, \\hatY_o\\right)+\\mathcalL_n e w\\left(Y_n, \\hatY_n\\right)+\\mathcalR\\left(\\hat\\theta_s, \\hat\\theta_o, \\hat\\theta_n\\right)\\right)
θs∗,θo∗,θn∗←θ^s,θ^o,θ^nargmin(λoLold(Yo,Y^o)+Lnew(Yn,Y^n)+R(θ^s,θ^o,θ^n))
第一项可以理解为old task的子优化目标,第二项为new task的优化目标,第三项为正则化项。
可以发现整个训练过程和joint training很相似,但是最大的不同是LWF没有用到old task data,而是巧妙地用KD损失去平衡old task的性能。至于KD则体现在以下公式:
L
o
l
d
(
y
o
,
y
^
o
)
=
−
H
(
y
o
′
,
y
^
o
′
)
=
−
∑
i
=
1
l
y
o
′
(
i
)
log
y
^
o
′
(
i
)
\\beginaligned \\mathcalL_o l d\\left(\\mathbfy_o, \\hat\\mathbfy_o\\right) &=-H\\left(\\mathbfy_o^\\prime, \\hat\\mathbfy_o^\\prime\\right) \\\\ &=-\\sum_i=1^l y_o^\\prime(i) \\log \\haty_o^\\prime(i) \\endaligned
Lold(yo,y^o)=−H(yo′,y^o′)=−i=1∑lyo′(i)logy^o′(i)
l
l
l 是label的数量,而
y
^
o
′
(
i
)
\\haty_o^\\prime(i)
y^o′(i) 和
y
o
′
(
i
)
y_o^\\prime(i)
yo′(i) 是
y
^
o
(
i
)
\\haty_o^(i)
y^o论文阅读 RSDNet: Learning to Predict Remaining Surgery Duration from Laparoscopic Videos Without Manual
论文阅读 RSDNet: Learning to Predict Remaining Surgery Duration from Laparoscopic Videos Without Manual
TensorFlow和深度学习入门教程(TensorFlow and deep learning without a PhD)
TensorFlow和深度学习入门教程(TensorFlow and deep learning without a PhD)