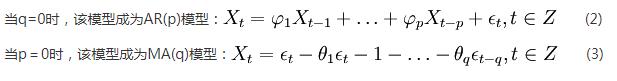ARIMA基本概念和流程讲解
Posted 早餐核桃牛奶
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了ARIMA基本概念和流程讲解相关的知识,希望对你有一定的参考价值。
基本概念



p: 自回归阶数
q: 滑动平均阶数
d: 时间序列成为平稳时所做的差分次数
AR - Auto Regression, 自回归模型:AR可以解决当前数据与后期数据之间的关系;表示为自回归模型 AR( p )
MA - Moving Average,移动平均模型:MA则可以解决随机变动也就是噪声的问题;表示为移动平均模型 MA(q)
ARMA - Auto Regression and Moving Average,自回归移动平均模型。自回归移动平均模型(ARMA)是与自回归(AR)和移动平均模型(MA)两部分组成;表示为ARMA(p, d)。(以上三类模型可以直接应用于平稳时间序列模型)
ARIMA - Auto Regression Integreate Moving Average,差分自回归移动平均模型。同前面的三种模型,ARIMA模型也是基于平稳的时间序列的或者差分化后是稳定的,另外前面的几种模型都可以看作ARIMA的某种特殊形式。表示为ARIMA(p, d, q)。(前面三种模型,d=0,即平稳时间序列模型不需要做差分)
ARIMA模型是在ARMA模型演变出来的,它实际上是先对数据做了差分,之后再使用ARMA模型;换句话说,ARIMA模型是先将非平稳数据变得平稳(用差分),之后再用ARMA模型处理平稳数据

基本流程
导入模型
import sys
import os
import warnings
warnings.filterwarnings("ignore")
import pandas as pd
import numpy as np
from arch.unitroot import ADF
import matplotlib.pylab as plt
%matplotlib inline
from matplotlib.pylab import style
style.use('ggplot')
import statsmodels.api as sm
import statsmodels.formula.api as smf
import statsmodels.tsa.api as smt
from statsmodels.tsa.stattools import adfuller
from statsmodels.stats.diagnostic import acorr_ljungbox
from statsmodels.graphics.api import qqplot
pd.set_option('display.float_format', lambda x: '%.5f' % x)
np.set_printoptions(precision=5, suppress=True)
"""中文显示问题"""
plt.rcParams['font.family'] = ['sans-serif']
plt.rcParams['font.sans-serif'] = ['SimHei']
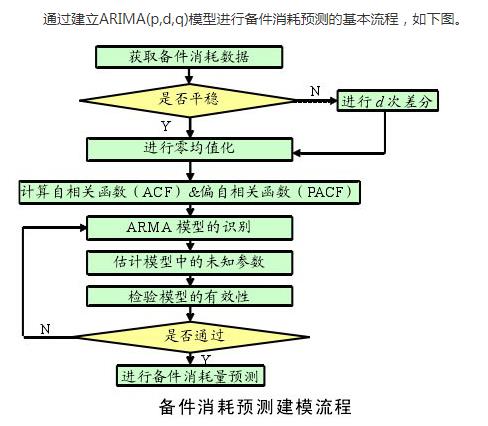
AR、MA和ARMA模型都必须是 “平稳非白噪声序列”,所以需要 “平稳性检验“ 和 “白噪声检验”
1.平稳性检验
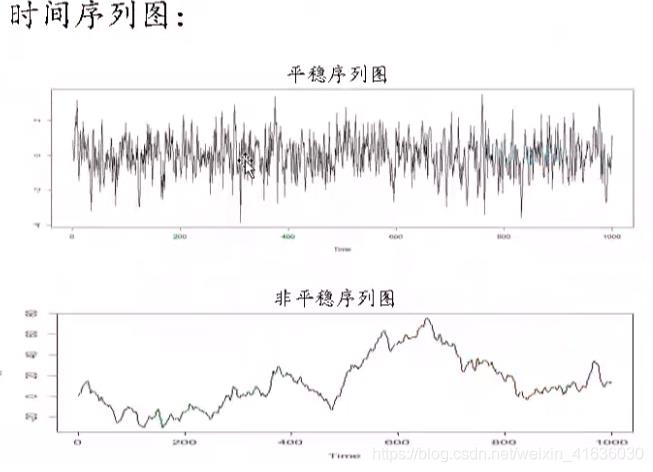
1)什么是序列平稳

2)检验是否平稳
第一和第二种方式很直观,但也很主观。它们全靠肉眼的判断和判断人的经验,不同的人看到同样的图形,很可能会给出不同的判断。
大部分情况选择第三种方法:单位根检验
方法一:观察序列图:若个体值要围绕序列均值上下波动,没有明显的上升或下降趋势,则是平稳序列。
如果出现上升或下降趋势,需要对原始序列进行差分平稳化处理在 3)不平稳序列转平稳序列部分,会讲如何差分平稳化
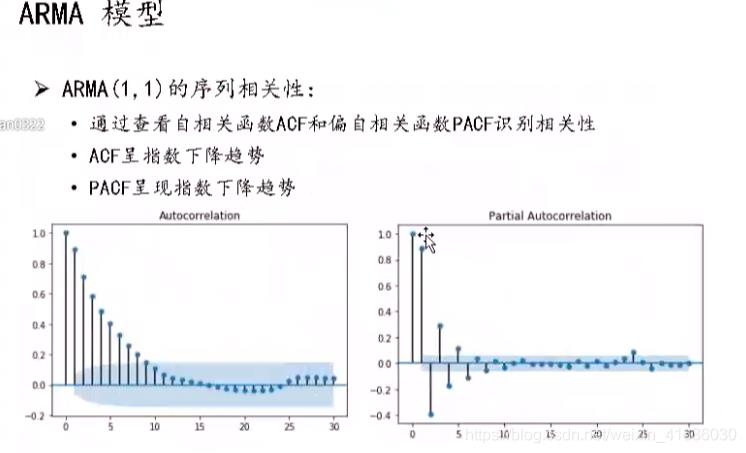
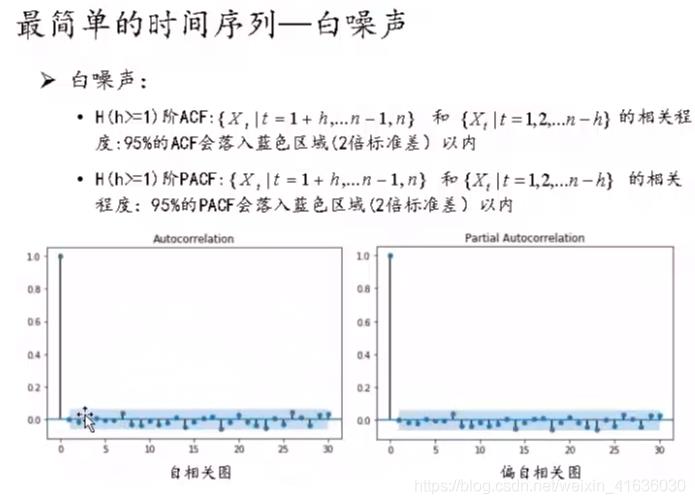
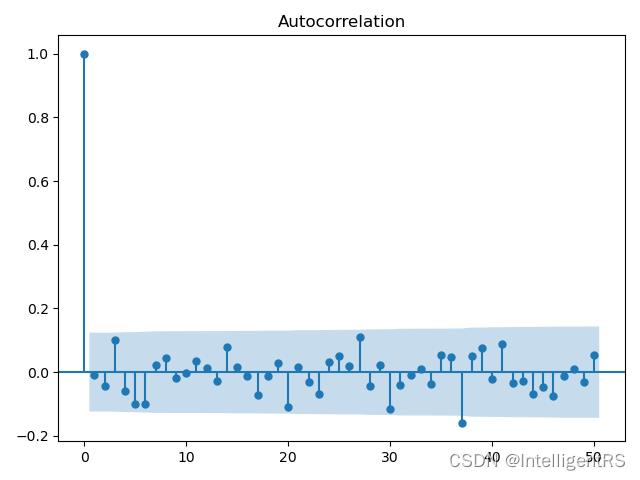
方法二:观察自相关图:平稳的序列的自相关图(ACF)和 偏相关图(PACF)不是拖尾就是截尾。
拖尾:始终有非零取值,不会在k大于某个常数后就恒等于零(或在0附近随机波动),顾名思义,就是序列缓慢衰减,“尾巴”慢慢拖着滑下来,:
截尾:在大于某个常数k后快速趋于0为k阶截尾,突然截断了,像个悬崖
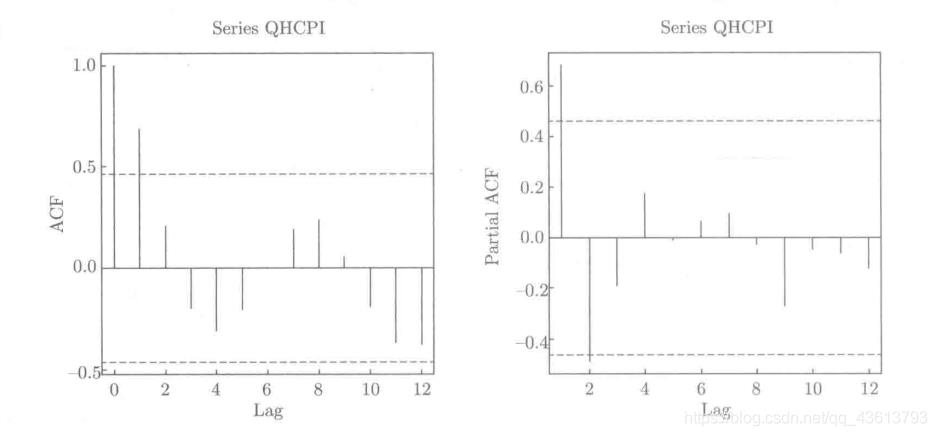
这张图可以看出,左图(自相关函数图)呈现出拖尾特征(2阶拖尾),而右图(偏自相关函数图)呈现出截尾特征(2阶截尾)
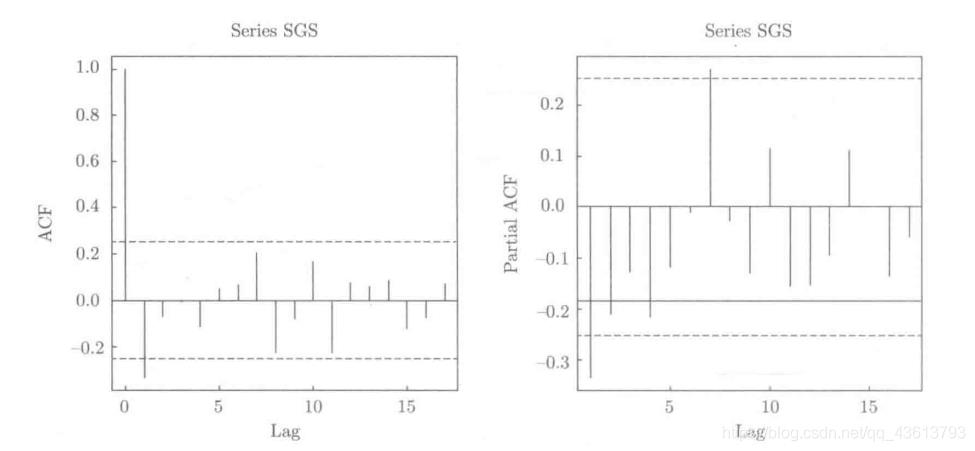
这张图可以看出,左图(自相关函数图)呈现出截尾特征(1阶截尾),而右图(偏自相关函数图)呈现出拖尾特征(1阶拖尾)

这张图可以看出,左图(自相关函数图)呈现出拖尾特征(2阶拖尾),右图(偏自相关函数图)也呈现出拖尾特征(1阶拖尾)
方法三:单位根检验:当一个时间序列的滞后算子多项式方程存在单位根时,我们认为该时间序列是非平稳的;反之,当该方程不存在单位根时,我们认为该时间序列是平稳的。
常见的单位根检验方法有DF检、ADF检验和PP检验,今天我们会用ADF检验来为大家演示
在Python中,有两个常用的包提供了ADF检验,分别是statsmodel和arch。
第一种方法:使用statsmodel的方法为:
from statsmodels.stats.diagnostic import unitroot_adf
unitroot_adf(df.pct_chg)
输出为:
这里包含了检验值、p-value、滞后阶数、自由度等信息。
我们看到了检验统计量为-14.46,远小于1%的临界值-3.47,即p值远小于0.01,因此我们拒绝原假设,认为该时间序列是平稳的。(这里原假设是存在单位根,即时间序列为非平稳的。)
第二种方法:使用arch的方法为:
from arch.unitroot import ADF
ADF(df.pct_chg)
其输出信息与statsmodel基本是一致的。
或
其他案例使用方法二
print("单位根检验:\\n")
print(ADF(data.diff1.dropna()))
单位根检验:
Augmented Dickey-Fuller Results
=====================================
Test Statistic -3.156
P-value 0.023
Lags 0
-------------------------------------
Trend: Constant
Critical Values: -3.63 (1%), -2.95 (5%), -2.61 (10%)
Null Hypothesis: The process contains a unit root.
Alternative Hypothesis: The process is weakly stationary.
单位根检验: 对其一阶差分进行单位根检验,得到:1%、%5、%10不同程度拒绝原假设的统计值和ADF Test result的比较,本数据中,P-value 为 0.023,接近0,ADF Test result同时小于5%、10%即说明很好地拒绝该假设,本数据中,ADF结果为-3.156,拒绝原假设,即一阶差分后数据是平稳的。
方法四:以上几个方法融合,即几种方法都做:结果更具有说服力
1.绘制时序图,观察是否存在波动和向上或向下的趋势
2.做相关系数图,若随时间间隔 k 增大,自相关系数迅速衰减则序列平稳;若随时间间隔 k 增大,自相关系数衰减缓慢则序列不平稳
3.进行单位根检验,P-值<α时,拒绝存在单位根的原假设,序列平稳。
3)不平稳序列转为平稳序列
取对数可以消除数据波动变大趋势
对数列进行差分,可以消除数据增长趋势性和季节性。
对于非平稳序列,如果先进行差分后的结果不满足要求,则需要在原有基础上继续进行差分,直到差分后的结果属于平稳性序列
方法:差分变换
fig = plt.figure(figsize=(12,8))
ax1= fig.add_subplot(111)
diff1 = dta.diff(1)
diff1.plot(ax=ax1)
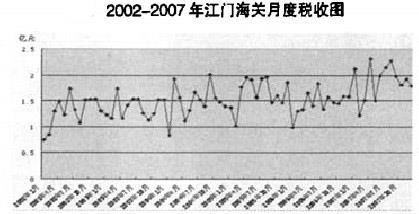
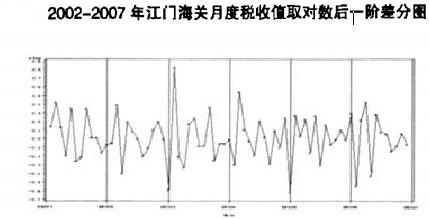
从下图可以看出,预测数列取对数并作一阶差分后的图形
选择其中一个检验方法,检验之后发现:
预测数列取对数并作一阶差分后的图形显示基本消除了长期趋势性的影响,趋于平稳化,满足ARIMA模型建模的基本要求。
2.白噪声检验
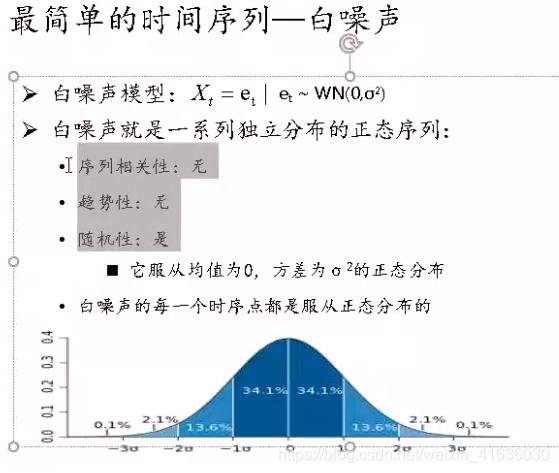
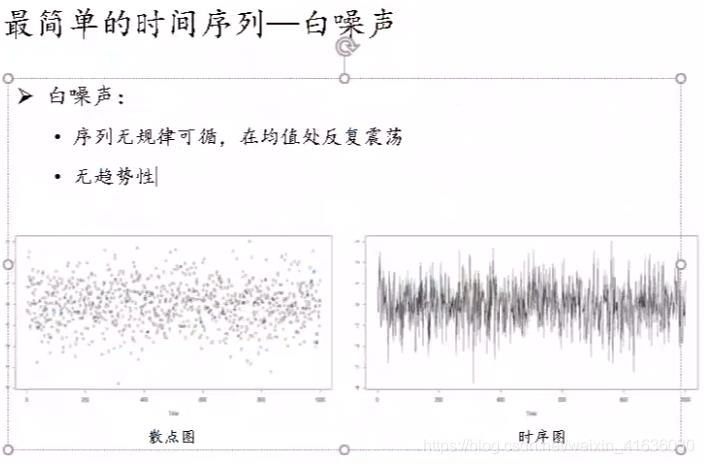
from statsmodels.stats.diagnostic import acorr_ljungbox
acorr_ljungbox(data.diff1.dropna(), lags = [i for i in range(1,12)],boxpierce=True)
(array([11.30402, 13.03896, 13.37637, 14.24184, 14.6937 , 15.33042,
16.36099, 16.76433, 18.15565, 18.16275, 18.21663]),
array([0.00077, 0.00147, 0.00389, 0.00656, 0.01175, 0.01784, 0.02202,
0.03266, 0.03341, 0.05228, 0.07669]),
array([10.4116 , 11.96391, 12.25693, 12.98574, 13.35437, 13.85704,
14.64353, 14.94072, 15.92929, 15.93415, 15.9696 ]),
array([0.00125, 0.00252, 0.00655, 0.01135, 0.02027, 0.03127, 0.04085,
0.06031, 0.06837, 0.10153, 0.14226]))
通过P<αP<α(α通常为0.05),拒绝原假设,故差分后的序列是平稳的非白噪声序列,可以进行下一步建模
3.模型定阶:计算自相关函数ACF 和 偏自相关函数PACF
若你检验方法选择方法二,则你已经得到了ACF和PACF,但检验方法最好还是选择单位根检验
流程:
1.根据ACF图和PACF图判断,序列平稳化后,使用AR、MA、ARMA中哪种模型
2.判断p,q阶数是多少
(前两步都是看ACF和PACF图来判断)
3.可能ARMA有多个p,q决定的模型(因为可能ACF和PACF图可以看出多个p和q),这时要通过信息标准AIC和BIC来协助选择模型
选择AIC、BIC值最小的,因为AIC、BIC越小,模型越好
但要注意的是,这些准则不能说明某一个模型的精确度,也即是说,对于三个模型A,B,C,我们能够判断出C模型是最好的,但不能保证C模型能够很好地刻画数据,因为有可能三个模型都是糟糕的。
赤池信息准则 (akaike information criterion) :AIC鼓励数据拟合的优良性但是尽量避免出现过度拟合(Overfitting)的情况。所以优先考虑的模型应是AIC值最小的那一个
贝叶斯信息准则 (bayesian information criterion) :
其中 L 是该模型下的最大似然, n 是数据数量, k 是模型的变量个数。


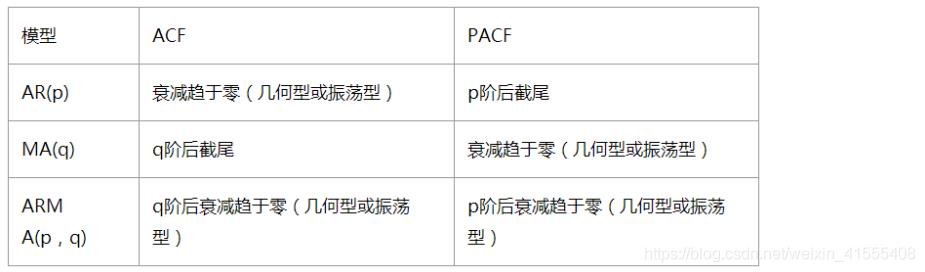
| 模型 | ACF | PACF |
|---|---|---|
| AR | 拖尾 | 截尾 |
| MA | 截尾 | 拖尾 |
| ARMA | 拖尾 | 拖尾 |
检查平稳时间序列的自相关图和偏自相关图。
通过sm.graphics.tsa.plot_acf和sm.graphics.tsa.plot_pacf得到图形
其中 lags 表示滞后的阶数,以上分别得到 ACF 图和 PACF 图
例子1:
1) 观察ACF和PACF图,判断是哪种模型
dta= dta.diff(1)#我们已经知道要使用一阶差分的时间序列,之前判断差分的程序可以注释掉
fig = plt.figure(figsize=(12,8))
ax1=fig.add_subplot(211)
fig = sm.graphics.tsa.plot_acf(dta,lags=40,ax=ax1)
ax2 = fig.add_subplot(212)
fig = sm.graphics.tsa.plot_pacf(dta,lags=40,ax=ax2)

通过两图观察得到:
- 自相关图显示滞后有三个阶超出了置信边界;
- 偏相关图显示在滞后1至7阶(lags 1,2,…,7)时的偏自相关系数超出了置信边界,从lag 7之后偏自相关系数值缩小至0 则有以下模型可以供选择:
- ARMA(0,1)模型:即自相关图在滞后1阶之后缩小为0,且偏自相关缩小至0,则是一个阶数q=1的移动平均模型;
- ARMA(7,0)模型:即偏自相关图在滞后7阶之后缩小为0,且自相关缩小至0,则是一个阶层p=3的自回归模型;
- ARMA(7,1)模型:即使得自相关和偏自相关都缩小至零。则是一个混合模型。
2) AIC BIC选择其中最佳模型
dta是差分后的序列
因为使用的是ARMA模型
arma_mod20 = sm.tsa.ARMA(dta,(7,0)).fit() # dta是差分后的序列
print(arma_mod20.aic,arma_mod20.bic,arma_mod20.hqic)
arma_mod30 = sm.tsa.ARMA(dta,(0,1)).fit()
print(arma_mod30.aic,arma_mod30.bic,arma_mod30.hqic)
arma_mod40 = sm.tsa.ARMA(dta,(7,1)).fit()
print(arma_mod40.aic,arma_mod40.bic,arma_mod40.hqic)
arma_mod50 = sm.tsa.ARMA(dta,(8,0)).fit()
print(arma_mod50.aic,arma_mod50.bic,arma_mod50.hqic)
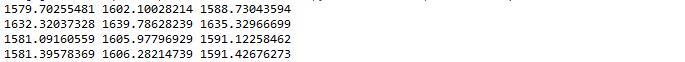
可以看到ARMA(7,0)的AIC,BIC,HQIC均最小,因此是最佳模型。
例子2:
1) 观察ACF和PACF图,判断是哪种模型
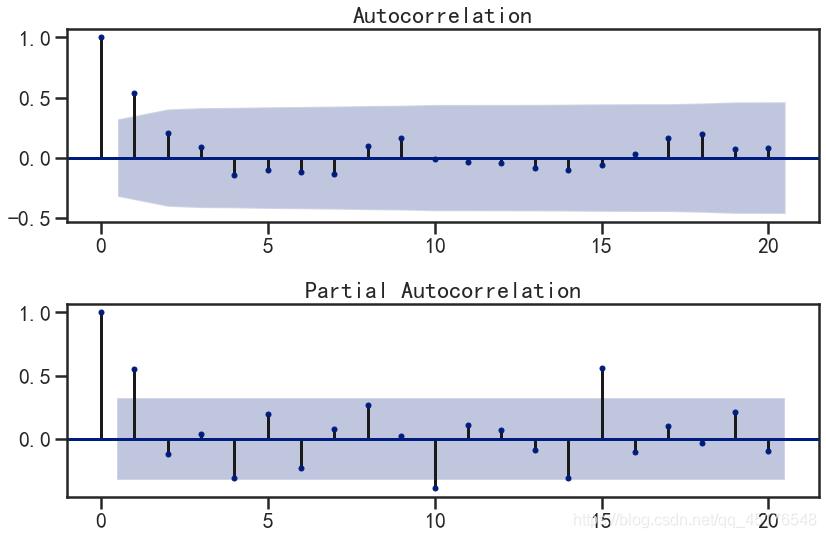
从一阶差分序列的自相关图和偏自相关图可以发现:
- 自相关图拖尾或一阶截尾
- 偏自相关图一阶截尾,
- 所以我们可以建立ARIMA(1,1,0)、ARIMA(1,1,1)、ARIMA(0,1,1)模型。
2) AIC BIC选择其中最佳模型
data[“xt”]是没有差分的序列
因为使用的是ARIMA模型
arma_mod20 = sm.tsa.ARIMA(data["xt"],(1,1,0)).fit() # data["xt"]是没有差分的数据
arma_mod30 = sm.tsa.ARIMA(data["xt"],(0,1,1)).fit()
arma_mod40 = sm.tsa.ARIMA(data["xt"],(1,1,1)).fit()
values = [[arma_mod20.aic,arma_mod20.bic,arma_mod20.hqic],[arma_mod30.aic,arma_mod30.bic,arma_mod30.hqic],[arma_mod40.aic,arma_mod40.bic,arma_mod40.hqic]]
df = pd.DataFrame(values,index=["AR(1,1,0)","MA(0,1,1)","ARMA(1,1,1)"],columns=["AIC","BIC","hqic"])
df
| AIC | BIC | hqic | |
|---|---|---|---|
| AR(1,1,0) | 253.09159 | 257.84215 | 254.74966 |
| MA(0,1,1) | 251.97340 | 256.72396 | 253.63147 |
| ARMA(1,1,1) | 254.09159 | 258.84535 | 259.74966 |
选择模型MA(0, 1, 1),即ARIMA(0, 1, 1)
4.参数估计
from statsmodels.tsa.arima_model import ARIMA
model = ARIMA(data["xt"], order=(0,1,1))
result = model.fit()
print(result.summary())
ARIMA Model Results
==============================================================================
Dep. Variable: D.xt No. Observations: 36
Model: ARIMA(0, 1, 1) Log Likelihood -122.987
Method: css-mle S.D. of innovations 7.309
Date: Tue, 22 Dec 2020 AIC 251.973
Time: 09:11:55 BIC 256.724
Sample: 01-01-1953 HQIC 253.631
- 01-01-1988
==============================================================================
coef std err z P>|z| [0.025 0.975]
------------------------------------------------------------------------------
const 4.9956 2.014 2.481 0.013 1.048 8.943
ma.L1.D.xt 0.6710 0.165 4.071 0.000 0.348 0.994
Roots
=============================================================================
Real Imaginary Modulus Frequency
-----------------------------------------------------------------------------
MA.1 -1.4902 +0.0000j 1.4902 0.5000
-----------------------------------------------------------------------------
5.模型检验

1) 参数的显著性检验


P<α(α通常为0.05),拒绝原假设,,认为该参数显著非零MA(2)模型拟合该序列,残差序列已实现白噪声
2)模型的显著性检验

resid = result.resid#残差
fig = plt.figure(figsize=(12,8))
ax = fig.add_subplot(111)
fig = qqplot(resid, line='q', ax=ax, fit=True)
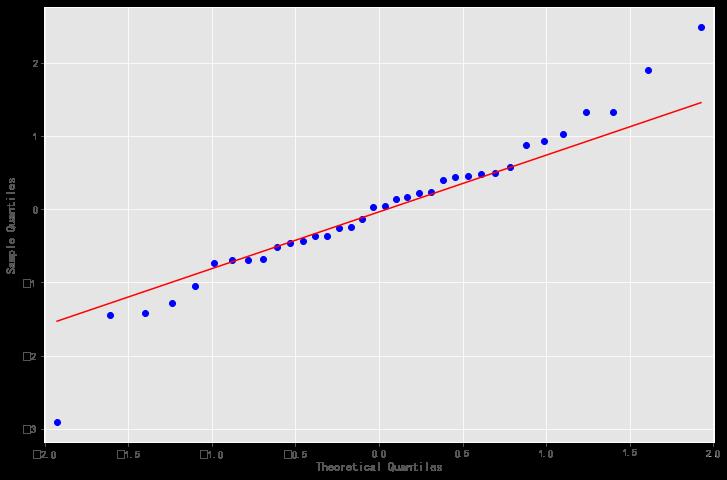
qq图显示,我们看到红色的KDE线与N(0,1)平行,这是残留物正太分布的良好指标,说明残差序列是白噪声序列,模型的信息的提取充分,当让大家也可以使用前面介绍的检验白噪声的方法LB统计量来检验
ARIMA(0,1,1)模型拟合该序列,残差序列已实现白噪声,且参数均显著非零。说明ARIMA(0,1,1)模型是该序列的有效拟合模型
6.模型预测
pred = result.predict('1988', '1990',dynamic=True, typ='levels')
print (pred)
1988-01-01 278.35527
1989-01-01 283.35088
1990-01-01 288.34649
Freq: AS-JAN, dtype: float64
plt.figure(figsize=(12, 8))
plt.xticks(rotation=45)
plt.plot(pred)
plt.plot(data.xt)
plt.show()
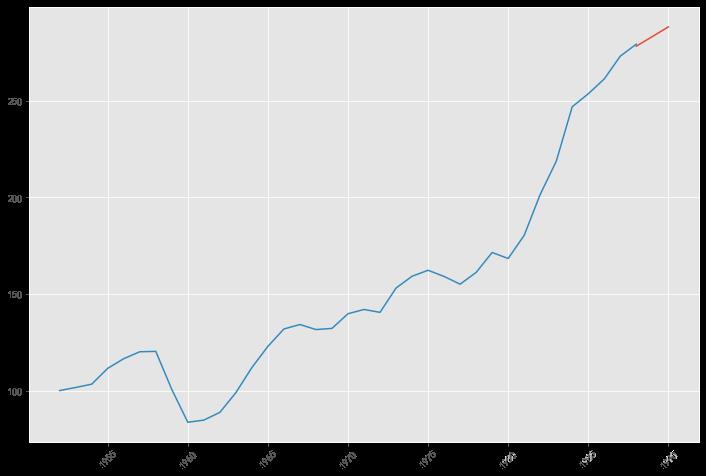
7.预测结果分析

平均绝对误差:
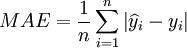
平均相对误差:
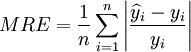
预测均方差:
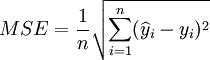
其中,y_i为序列的实际数据,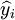 为模型预测数据。
为模型预测数据。
例如:
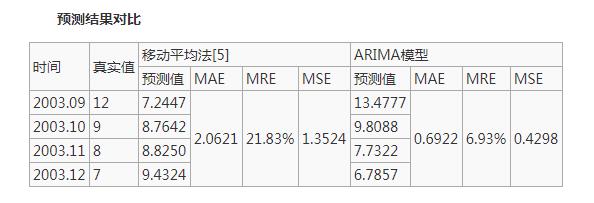
由上表预测结果及各项评价指标的对比可知,ARIMA模型预测结果明显优于移动平均法,从平均相对误差上来看,ARIMA模型为6.93%,比移动平均法提高了将近15%,且预测的均方差也较小,仅0.4298。由此可见:该模型能较准确地预测出备件消耗的变化趋势,可为备件消耗量的预测提供依据。
引用:
https://blog.csdn.net/qixizhuang/article/details/86716149
https://zhidao.baidu.com/question/288273884.html
https://zhuanlan.zhihu.com/p/343617191
https://blog.csdn.net/qq_43613793/article/details/109908418
https://blog.csdn.net/qq_45176548/article/details/116771331
https://blog.csdn.net/weixin_41555408/article/details/117218457
https://blog.csdn.net/weixin_41636030/article/details/89138638
https://www.zhihu.com/question/48447779/answer/112330897
https://blog.csdn.net/u010414589/article/details/49622625
https://wiki.mbalib.com/wiki/ARIMA%E6%A8%A1%E5%9E%8B
https://blog.csdn.net/qq_45176548/article/details/111504846
时间序列模型-ARIMA
一、ARIMA模型基本概念
1.1 自回归模型(AR)
- 描述当前值与历史值之间的关系,用变量自身的历史数据对自身进行预测;
- 自回归模型必须满足平稳性的要求;(何为平稳性:见时间序列数据分析基本概念)
- p阶自回归过程的公式定义:
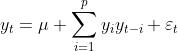
其中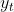 是当前值,
是当前值,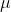 是常数项,p是阶数,
是常数项,p是阶数,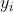 是自相关系数,
是自相关系数,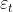 是误差。
是误差。
1.1.1 自回归模型的限制
- 自回归模型是用自身的数据来进行预测;
- 必须具有平稳性;
- 必须具有自相关性,如果自相关系数
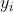 小于0.5,则不宜采用;
小于0.5,则不宜采用; - 自回归只适用于预测与自身前期相关的现象;
1.2 移动平均模型(MA)
- 移动平均模型关注的是自回归模型中的误差项的累加;
- 移动平均法能有效的消除预测中的随机波动;
- q阶自回归过程的公式定义:

1.3 自回归移动平均模型(ARMA)
自回归与移动平均的结合,公式定义:

1.4 差分自回归移动平均模型(ARIMA)
ARIMA(p,d,q)模型全称为差分自回归移动平均模型(Autoregressive Integrated Moving Average Model,简记ARIMA)
- AR是自回归,p为自回归项;MA为移动平均,q为移动平均项,d为时间序列成为平稳时所做的差分次数;
- 原理:将非平稳时间序列转化为平稳时间序列,然后因变量仅对它的滞后值以及随机误差项的现值和滞后值进行回归所建立的模型;
1.5 自相关函数ACF(autocorrelation function)
- 有序的随机变量序列与自身相比较,自相关函数反映了同一序列在不同时序的取值之间的相关性;
- 公式:
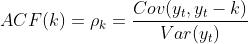
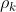 的取值范围为[-1,1]。
的取值范围为[-1,1]。
1.6 偏自相关函数PACF(partial autocorrelation function )
- 对于一个平稳AR(p)模型,求出滞后k自相关系数p(k)时,实际上得到的并不是x(t)与x(t-k)之间单纯的相关关系;
- x(t)同时还会受到中间k-1个随机变量x(t-1),x(t-2),...,x(t-k+1)的影响,而这k-1个随机变量又都和x(t-k)具有相关关系,所以自相关系数p(k)里实际掺杂了其他变量对x(t)与x(t-k)的影响
- 剔除了中间k-1个随机变量x(t-1),x(t-2),...,x(t-k+1)的干扰之后x(t-k)对x(t)影响的相关程度;
- ACF还包含了其他变量的影响,而偏自相关系数PACF是严格这两个变量之间的相关性;
1.7 ARIMA(p,d,q)阶数确定
AR(p)看PACF,MA(q)看ACF
| 模型 | ACF | PACF |
| AR(p) | 衰减趋于零(几何型或振荡型) | p阶后截尾 |
| MA(q) | q阶后截尾 | 衰减趋于零(几何型或振荡型) |
| ARMA(p,q) | q阶后衰减趋于零(几何型或振荡型) | p阶后衰减趋于零(几何型或振荡型) |
截尾:落在置信区间内(95%的点都符合该规则)
1.8 ARIMA建模流程
- 获取被观测系统时间序列数据;
- 对数据绘图,观测是否为平稳时间序列;对于非平稳时间序列要先进行d阶差分运算,化为平稳时间序列;
- 经过第二步处理,已经得到平稳时间序列。要对平稳时间序列分别求得其自相关系数ACF 和偏自相关系数PACF ,通过对自相关图和偏自相关图的分析,得到最佳的阶层 p 和阶数 q;
- 由以上得到的 ,得到ARIMA模型。然后开始对得到的模型进行模型检验。
1.9 模型选择AIC与BIC:选择更简单的模型
- AIC:赤池信息准则(Akaike Information Criterion,AIC)

- BIC:贝叶斯信息准则(Bayesian Information Criterion,BIC)
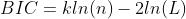
k为模型参数个数,n为样本数量,L为似然函数;在保证模型精度的情况下尽量使得k值越小越好。
1.10 模型残差检验
- ARIMA模型的残差是否是平均值为0且方差为常数的正态分布;
- QQ图:线性即正态分布;
二、pandas数据处理
2.1 pandas数据重采样
date_range
- 可以指定开始时间与周期
- H:小时
- D:天
- M:月
import pandas as pd
import numpy as np
rng = pd.date_range("2016/07/01",periods=10,freq="D")
print(rng)
time = pd.Series(np.random.randn(20),index=pd.date_range("2016/1/1",periods=20))
print(time)
数据重采样:
- 时间数据由一个频率转换到另一个频率
- 降采样
- 升采样
rng = pd.date_range("2011/1/1",periods=90,freq="D")
ts = pd.Series(np.random.randn(len(rng)),index=rng)
print(ts)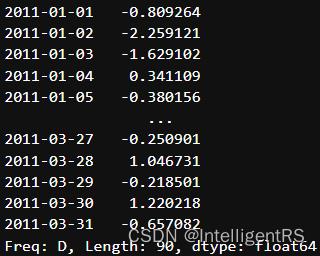
ts.resample("3D").sum()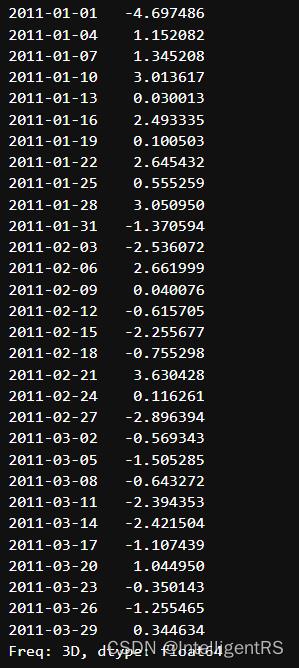
升采样插值方法
- ffill空值取前面的值
- bfill空值取后面的值
- interpolate 线性取值
day3D.resample("D").ffill(2)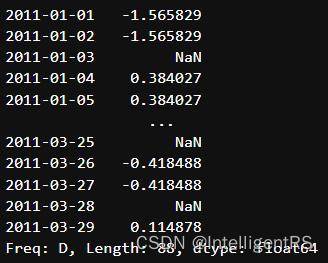
day3D.resample("D").interpolate("linear") 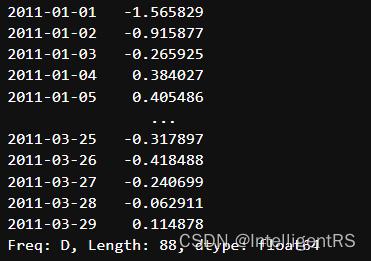
2.2 Pandas滑动窗口
r = ts.rolling(window=10).mean()
print(r)
import matplotlib.pyplot as plt
plt.figure(figsize=(15,5))
ts.plot(style="r--")
ts.rolling(window=10).mean().plot(style="b")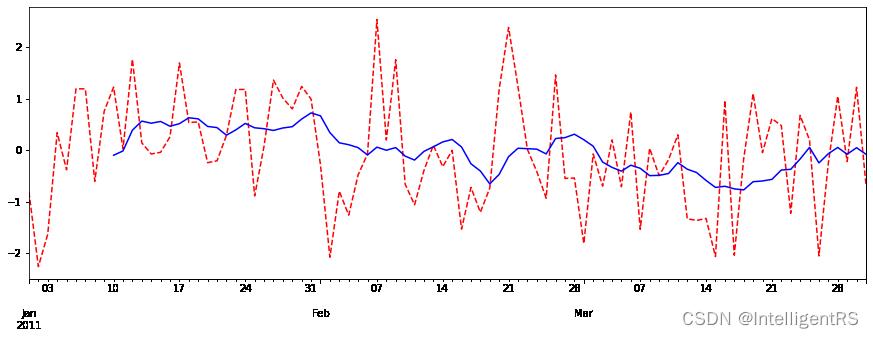
以上是关于ARIMA基本概念和流程讲解的主要内容,如果未能解决你的问题,请参考以下文章