数字图像处理学习--导数运算与锐化空间滤波

Posted 2022-03-09 LaoYuanPython

引言

本文内容是老猿学习冈萨雷斯《数字图像处理》后的学习总结和感悟，中文版在介绍本文内容时翻译存在比较多的问题，本文是对中文版的完善、补充以及学习感悟的总结。在学习过程中对一些细节进行了一些思考耽误了一些时间，不过也将这些思考单独发布了博文赚点原力值。

一、锐化处理简介

锐化空间滤波器（Sharpening Spatial Filters），用于图像锐化处理（sharpening）的主要目的是突出灰度的过渡部分（highlight transitions in intensity）。图像锐化（image sharpening）的用途多种多样，应用范围从电子印刷(electronic printing )和医学成像(medical imaging)到工业检测(industrial inspection)和军事系统的制导(autonomous guidance in military systems)等。

在《数字图像处理：线性和非线性滤波的平滑空间滤波器（Smoothing Spatial Filters）》中，介绍了图像模糊可通过在空间域用像索邻域平均法实现。因为均值处理与积分（integration）类似（老猿注：请参考《为什么说图像均值处理与积分类似？》），而图像锐化的处理与图像模糊是相反的操作，因此在逻辑上，我们可以得出锐化处理可由空间微分（spatial differentiation）来实现这一结论。事实上，的确如此，本文将讨论由数字微分（digital differentiation）来定义和实现锐化算子的各种方法。

二、锐化空间滤波器与导数运算的关系

2.1、导数、微分相关概念

在开始介绍前，有三个名词术语的翻译对介绍会有一定的影响，中文版翻译有些问题，老猿考究了一下，将其理清如下：

1. 微分：英文 differential，函数f(x)的微分表示为df(x)，df(x)=f’(x)dx，更多介绍请参考《人工智能数学基础–微分：定义、运算以及应用》；
2. 导数：英文 derivative，函数f(x)的导数表示为f’(x)，f’(x)=df(x)/dx，因此导数又称为微商，更多介绍请参考《人工智能数学基础–导数1：基础概念及运算》。
3. 微分运算：英文 differentiation，通常是指求导、求微分的运算。

关于微分和导数的概念有时分不清，二者的关系请参考《一元函数中的导数、微分和不定积分的关系》的介绍。

2.2、图像处理导数运算应该达到的效果

在讨论具体滤波器之前，先回顾一下数字意义上导数（derivatives）的某些基本性质。为简化说明，我们主要集中讨论一阶导数（one-dimensional derivatives）的性质。

图像锐化处理时，我们最感兴趣的是恒定灰度区域中，突变（discontinuities，包括台阶和斜坡突变，step and ramp discontinuities，相关概念请参考《灰度斜坡intensity ramp和灰度台阶intensity step的区别》的介绍）的开始点（onset）与结束点及沿着灰度斜坡处（intensity ramps）的求导表现（behavior of these derivatives）。这些类型的突变可以用来对图像中的噪声点、线与边缘建模。进入或退出这些图像变化过程所包含的导数性质（behavior of derivatives）也很重要。

数字函数（digital function）的导数（derivatives）可以用不同的术语定义，也有各种方法定义这些差别。然而对于一阶导数（first derivative）的任何定义都必须保证以下几点性质：

1. 在恒定灰度区域（constant intensity）的值为零；
2. 在灰度台阶或斜坡的开始处（at the onset of an intensity step or ramp）值非零；
3. 沿着斜坡（along ramps）的值非零。

老猿注：在图像处理中的一阶导数，就是求图像灰度变化曲线的导数，反映的是灰度变化情况，能够突出图像中的对象边缘。

类似地，任何二阶导数（second derivative）的定义必须保证以下几点性质：

1. 在恒定区域（constant areas）值为零；
   老猿注：这里的恒定区域与恒定灰度应该是有区别的，恒定灰度要求的灰度是没有变化，恒定区域老猿理解要求的是灰度没有突变只有灰度匀速线性变化。
2. 在灰度台阶或斜坡的起点处和终点处（at the onset and end of an intensity step or ramp）值非零;
3. 沿着恒定坡度的斜坡（along ramps of constant slope）的值为零。

老猿注：上面对于图像一阶导数和二阶导数的要求的中文版翻译存在问题的，所以老猿进行了调整。

除了算子取值的区别外，基于这些数值区别可以得到更多的结论，具体请参考《一阶导数/微分和二阶导数/微分算子在图像锐化处理方面的区别》。

基本上，求导运算（derivative operator）的响应强度与图像在用算子操作的这一点的突变程度成正比，这样，图像微分增强（image differentiation enhances）边缘（edges）和其他突变(discontinuities，如噪声)，而削弱（deemphasizes）灰度变化缓慢（slowly varying intensities）的区域。

2.3、图像处理导数运算的公式

因为数字图像处理的是数字量（digital quantities），其值是有限的，故最大灰度级的变化也是有限的，并且变化发生的最短距离是在两相邻像素之间。

对于一维函数f(x)，其一阶导数的基本定义是差值（difference）：

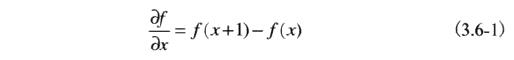
式 3.6-1 左边用的是偏导数（partial derivative）方式的表示，是因为图像坐标有两个变量，是二维函数，其导数是二维函数，为了与二维函数导数表示一致，因此用了偏导数的表示方式。当函数f(x)只有一个变量时，∂f/∂x=df/dx。

老猿注：

1. 相关缘由请参考《为什么说数字图像的一阶微分为f(x+1)-f(x)?》的介绍。
2. 上式等式右边也可以写成：f(x)-f(x-1)，因为增量可以为正值也可以为负值。

对于一维函数f(x)，其二阶导数的基本定义是差值：

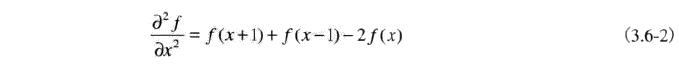
这个推导由导数四则运算即可推导出来，具体过程请参考《数字图像处理中一元函数f(x)的二阶导数=f(x+1)+f(x-1)-2f(x)的由来》。

很容易验证，式3.6-1和3.6-2满足图像处理导数运算应该达到的效果要求，公式也确实是求导方式推导出来的。

2.4、一阶导数和二阶导数图像影响案例

下图3.36(b)(图的中间)显示了一段扫描线。小方块中的数值是扫描线中的灰度值，它们作为黑点画在上方的图3.36(a)中。用虚线连接这些点是为了帮助我们看得更清楚。正如图中所示，扫描线包含一个灰度斜坡、三个恒定灰度段和一个灰度台阶。圆圈指出了灰度变化的起点和终点。用前面两个定义计算出的图3.36(b)中扫描线的一阶微分和二阶微分画在图3.36©中。

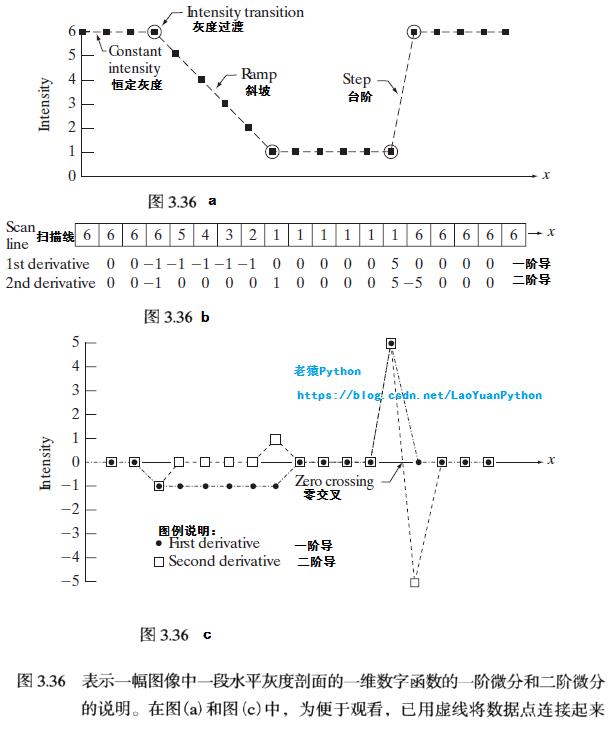
当在点x处计算一阶微分时，我们用下一个点的函数值减去该点的函数值。因此，这是一个“预测未来”(look-ahead)的操作。类似地，为了在x点计算二阶微分，在计算中我们使用前一个点和下一个点。为了避免前一个点和下一个点处于扫描线之外的情况，我们在图3.36中显示了从序列中第二个点到倒数第二个点的微分计算。

让我们从左到右横贯剖面(profile)图，考虑前面部分介绍的一阶导数和二阶导数的性质：

1. 首先，我们遇到的是如图3.36(b)和©所示的恒定灰度区域，一阶导数和二阶导数都是零，因此，两者都满足条件(1)；
2. 接着，我们遇到紧随台阶的一个灰度斜坡，并且我们注意到在斜坡起点和台阶处的一阶导数不为零；
   类似地，在斜坡和台阶的起点和终点的二阶导数也不为零;因此，两个导数特性都满足条件(2)；
3. 最后，我们看到，两个导数特性也都满足条件(3)，因为对于斜坡来说一阶导数不是零，二阶导数是零。

请注意斜坡或台阶的起点和终点处二阶导数的符号变化。事实上，我们在图3.36©中看到，在一个台阶的过渡中，连接这两个值的线段在两个端点的中间与水平轴相交，这是零交叉（zero crossing）特征，对于边缘定位是非常有用的，将在后续博文中介绍。

数字图像中的边缘在灰度上常常类似于斜坡过渡（ramp-like transitions），这样就导致图像的一阶导数产生较粗的边缘，因为沿着斜坡的导数非零。另一方面，二阶导数产生由零分开(separated by zeros)的一个像素宽的双边缘（double edge one pixel thick)。由此，我们得出结论，二阶导数在增强细节方面要比一阶导数好得多，这是一个适合锐化图像的理想特性。同时二阶导数比一阶导数执行上要容易得多，因此我们主要关注二阶导数。

老猿注：就像零交叉特征那样，由于二阶导数在斜坡的起点和终点（如图像边缘）会有正值和负值的变化，在边缘内部的像素之间二阶导数会为0，正值和负值都会对应到一个边缘，而中间由0分隔，因此会产生由零分开的一个像素宽的双边缘。

三、小结

本文介绍了图像锐化空间滤波器的基本概念，定义了数字图像处理一阶导和二阶导的公式，以及锐化处理与数字图像函数导数的关系，通过介绍，可以理解数字图像的二阶导数比较适合图像锐化处理。

更多图像处理请参考专栏《OpenCV-Python图形图像处理》、《图像处理基础知识》以及付费专栏《OpenCV-Python初学者疑难问题集》的介绍。

对于缺乏Python基础的同仁，可以通过老猿的免费专栏《 专栏：Python基础教程目录》从零开始学习Python。

如对文章内容存在疑问，可在博客评论区留言，或关注：老猿Python 微信公号发消息咨询：

也可以扫描博客左边栏目的微信公号二维码咨询。

写博不易，敬请支持：

如果阅读本文于您有所获，敬请点赞、评论、收藏，谢谢大家的支持！

关于老猿的付费专栏

1. 付费专栏《https://blog.csdn.net/laoyuanpython/category_9607725.html 使用PyQt开发图形界面Python应用》专门介绍基于Python的PyQt图形界面开发基础教程，对应文章目录为《 https://blog.csdn.net/LaoYuanPython/article/details/107580932 使用PyQt开发图形界面Python应用专栏目录》；
2. 付费专栏《https://blog.csdn.net/laoyuanpython/category_10232926.html moviepy音视频开发专栏 )详细介绍moviepy音视频剪辑合成处理的类相关方法及使用相关方法进行相关剪辑合成场景的处理，对应文章目录为《https://blog.csdn.net/LaoYuanPython/article/details/107574583 moviepy音视频开发专栏文章目录》；
3. 付费专栏《https://blog.csdn.net/laoyuanpython/category_10581071.html OpenCV-Python初学者疑难问题集》为《https://blog.csdn.net/laoyuanpython/category_9979286.html OpenCV-Python图形图像处理 》的伴生专栏，是笔者对OpenCV-Python图形图像处理学习中遇到的一些问题个人感悟的整合，相关资料基本上都是老猿反复研究的成果，有助于OpenCV-Python初学者比较深入地理解OpenCV，对应文章目录为《https://blog.csdn.net/LaoYuanPython/article/details/109713407 OpenCV-Python初学者疑难问题集专栏目录 》
4. 付费专栏《https://blog.csdn.net/laoyuanpython/category_10762553.html Python爬虫入门 》站在一个互联网前端开发小白的角度介绍爬虫开发应知应会内容，包括爬虫入门的基础知识，以及爬取CSDN文章信息、博主信息、给文章点赞、评论等实战内容。

前两个专栏都适合有一定Python基础但无相关知识的小白读者学习，第三个专栏请大家结合《https://blog.csdn.net/laoyuanpython/category_9979286.html OpenCV-Python图形图像处理 》的学习使用。

对于缺乏Python基础的同仁，可以通过老猿的免费专栏《https://blog.csdn.net/laoyuanpython/category_9831699.html 专栏：Python基础教程目录）从零开始学习Python。

如果有兴趣也愿意支持老猿的读者，欢迎购买付费专栏。

老猿Python，跟老猿学Python！

☞ ░ 前往老猿Python博文目录 https://blog.csdn.net/LaoYuanPython ░