Euclidean, Manhattan, hop-count distance 区别
Posted 软件工程小施同学
tags:
篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了Euclidean, Manhattan, hop-count distance 区别相关的知识，希望对你有一定的参考价值。
欧式距离（Euclidean Distance）
二维空间的公式
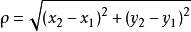
其中，
为点
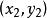与点
之间的欧氏距离；
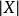为点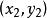 到原点的欧氏距离。
曼哈顿距离（Manhattan Distance ）
两点在南北方向上的距离加上在东西方向上的距离，即d(i,j)=|xi-xj|+|yi-yj|
跳段距离hop-count distance
一个节点到另一个节点经过的节点个数 称为两个节点间的 跳段距离
以上是关于Euclidean, Manhattan, hop-count distance 区别的主要内容，如果未能解决你的问题，请参考以下文章